Archives de catégorie : Sciences

Je donne ici la version française d’un entretien que j’ai eu avec l’excellent journaliste franco-slovaque Vivien Cosculluela, paru en langue slovaque dans le magazine Plus 7 dni le 3 février 2025.

Le trou noir est entré dans l’imaginaire collectif. Chacun se représente sa propre version de cette manifestation physique et l’utilise en lui donnant les attributs dont il a besoin dans son discours. Quelles sont les raisons de ce passage du trou noir de la science au langage courant ?

L’imaginaire humain. La description scientifique du trou noir nous dit que c’est un piège gravitationnel, un puits sans fond, puisqu’on y tombe sans pouvoir en ressortir. Cela correspond à un archétype de l’esprit humain de la fin de toute chose. On trouve des textes littéraires et poétiques qui évoquent de façon extrêmement frappante des équivalents à ce que l’astrophysique appelle aujourd’hui des trous noirs.

Lesquels ?

En 1854 le poète français Gérard de Nerval, dans Le Christ aux Oliviers, décrit de façon incroyable un puits sombre où les mondes, les jours tourbillonnent et s’engouffrent, à une époque où on ne parlait pas de ces objets astrophysiques.

Du tout ?

Le concept d’astre invisible, mais pas vraiment de piège gravitationnel, avait été imaginé à la fin du dix-huitième siècle, mais l’idée avait été complètement oubliée à l’époque romantique. Pourtant, on trouve, en autres chez de Nerval et chez l’Allemand Jean Paul, des descriptions fascinantes de cette idée d’un lieu de l’univers où toutes choses s’engouffrent sans retour.

Quand cette idée a-t-elle de nouveau éclos ?

Le concept astrophysique de trou noir n’a émergé de nouveau qu’au vingtième siècle avec la théorie d’Albert Einstein, la relativité générale. Il y a cependant eu beaucoup d’obstacles, y compris dans le monde scientifique, à commencer par la résistance du père de la relativité lui-même, qui n’a jamais vraiment voulu admettre que ces objets aux propriétés effectivement assez bizarres et contre-intuitives puissent exister. Aujourd’hui, ils sont devenus des corps célestes très médiatisés.

Depuis quand ?

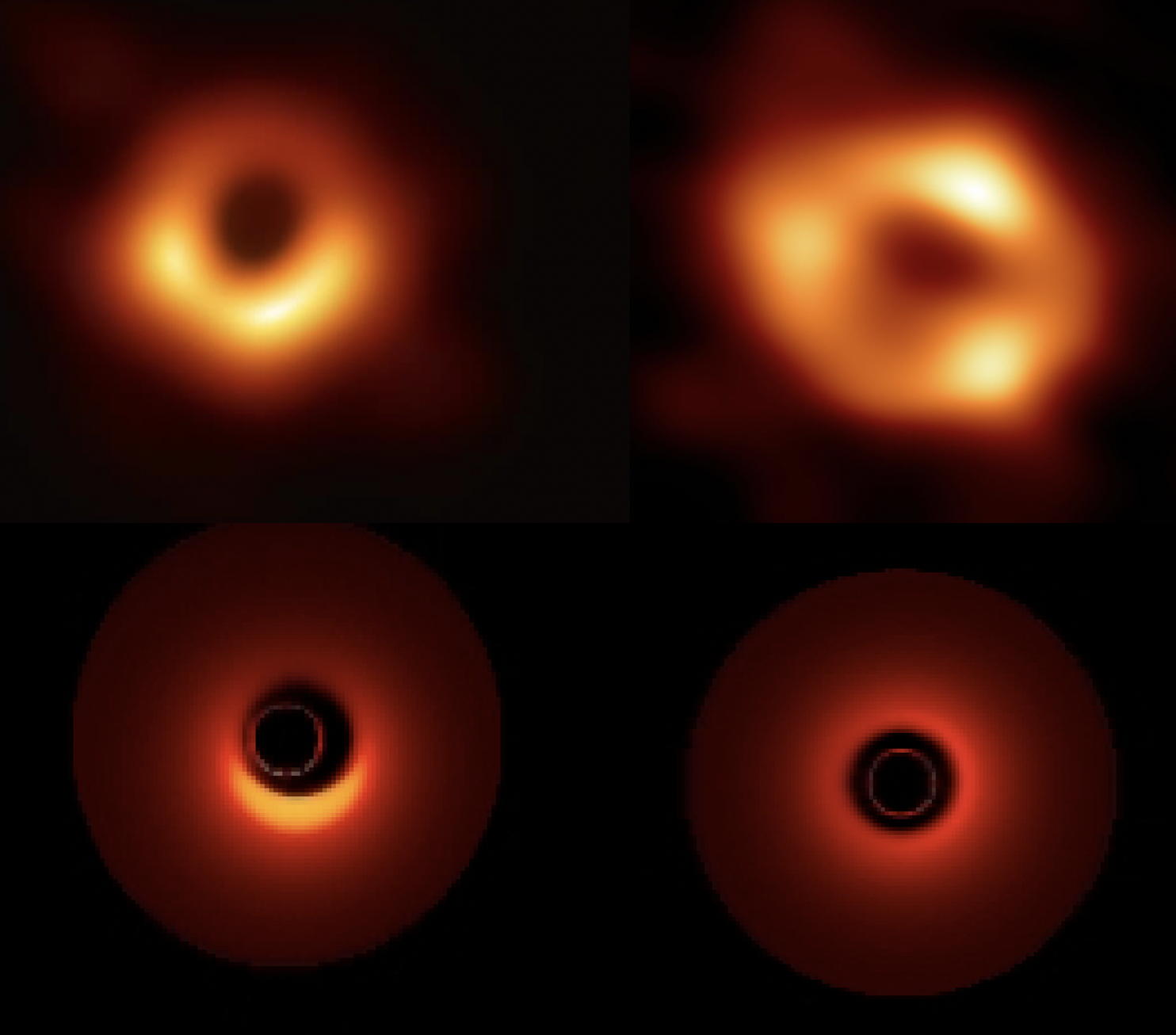
Quand j’ai commencé mes premiers travaux sur les trous noirs, à la fin des années 70, ils avaient déjà un statut théorique relativement solide, mais un statut expérimental, sur le plan observationnel, extrêmement faible. Celui-ci a évolué, au point que l’on pense en avoir des images télescopiques. Mais il a fallu des décennies pour que ce concept soit plus ou moins accepté, bien que toujours pas totalement.

Comment les puits gravitationnels se forment ?

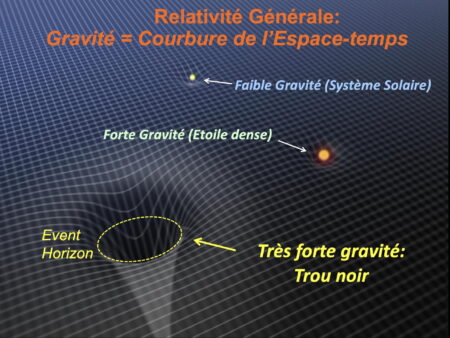
Ce n’est pas un trou que l’on fait dans la Terre ou dans l’espace, c’est la gravitation qui creuse ce puits. J’utilise souvent l’image du tissu élastique de l’espace et du temps. La relativité générale nous explique que l’espace-temps n’est pas une structure rigide comme on le croyait depuis Newton, mais une structure souple et élastique dont les formes sont dictées par la présence de corps massifs. Donc, un corps plus compact génère des déformations plus importantes du tissu élastique. Cela se traduit mathématiquement par les équations d’Einstein.

Et ces déformations deviennent des trous noirs ?

Plus le degré de compacité du corps est grand, plus la déformation est importante, jusqu’au cas extrême qu’on appelle effondrement gravitationnel. Le degré de compacité, donc la distorsion, sont tels qu’il se forme une zone de non-retour, marquant l’entrée de ce puits de gravitation. La matière tombe ensuite dedans, mais n’a plus assez d’énergie pour en sortir, y compris la lumière. C’est la définition relativiste d’un trou noir.

Est-ce qu’il y a aussi parfois une incompréhension de ce que c’est ?

On lit malheureusement souvent, et cela a longtemps nui d’ailleurs à l’acceptation du concept, que c’est une singularité, c’est-à-dire un point infiniment petit où tout s’écrase indéfiniment. C’est une absurdité physique.

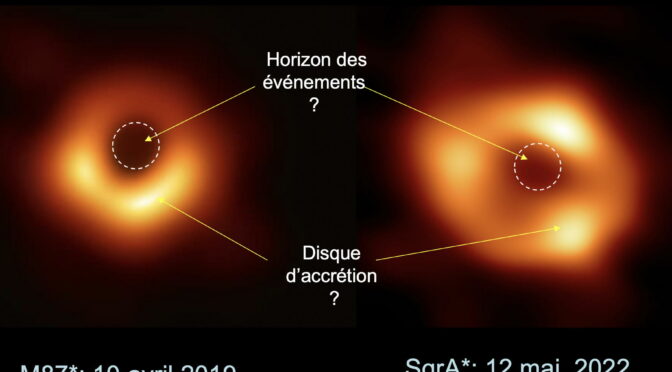
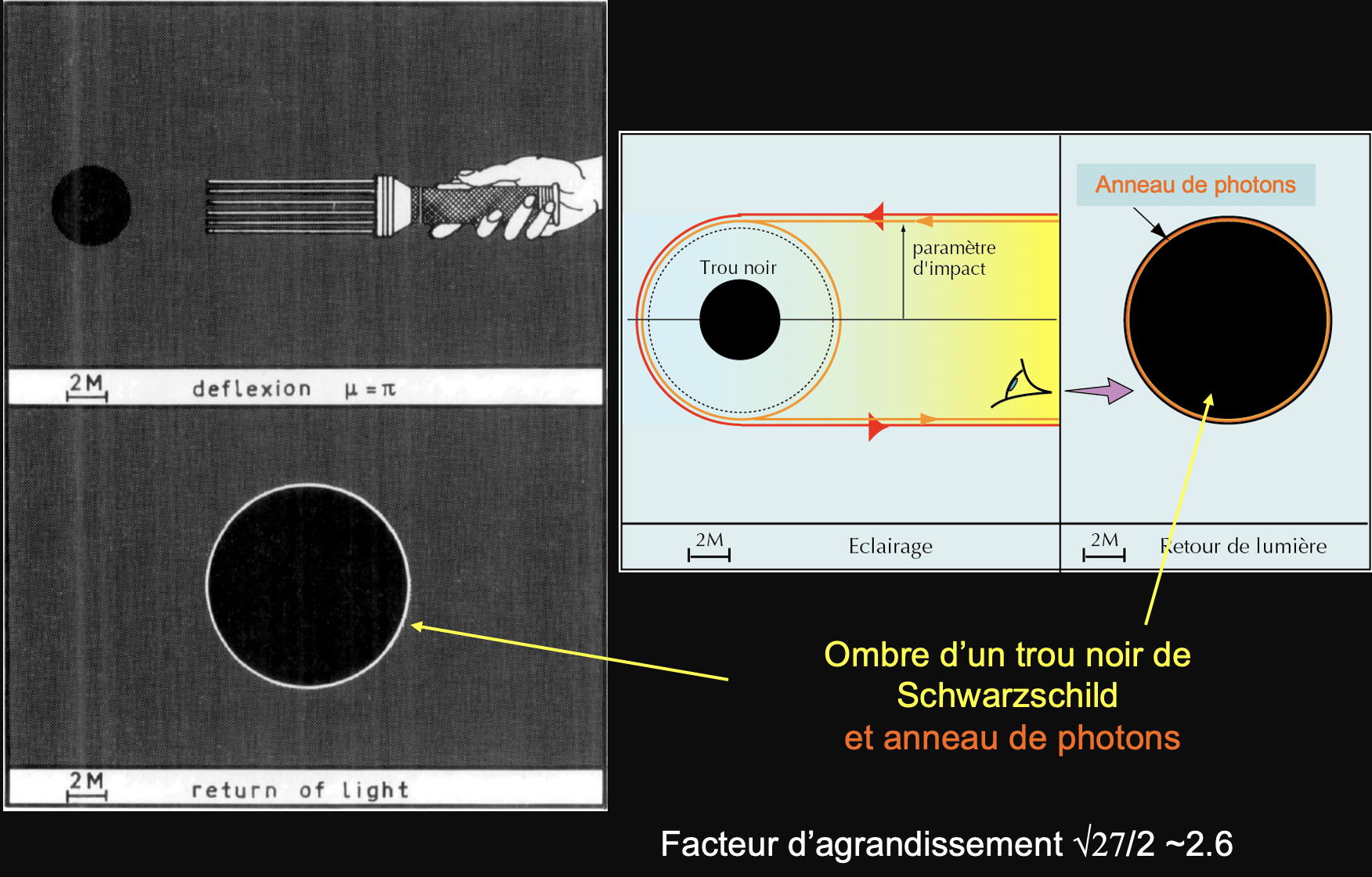
Que voit-on de ce phénomène ?

On ignore ce qu’il se passe à son centre, mais on voit sa surface, que l’on appelle un horizon des événements, c’est-à-dire la frontière du puits, qui est purement géométrique et immatérielle. Ce n’est pas une surface solide comme celle des étoiles à neutrons ou des naines blanches, c’est-à-dire des autres étoiles compactes qui se sont effondrées gravitationnellement, mais dont l’effondrement a été stoppé par une résistance de la matière.

Pour les trous noirs il ne s’est donc pas arrêté ?

Les lois de la physique nous disent qu’au-delà d’une certaine masse critique, qui est de l’ordre de trois fois celle du soleil, l’effondrement ne peut pas être arrêté par une résistance de la matière, quelle que soit sa nature. D’où cette idée d’effondrement qui va déconnecter l’objet qui s’effondre de l’espace-temps extérieur, la déconnexion se faisant à travers l’horizon des événements.

Pourquoi ce terme d’horizon des événements ?

Les événements, c’est-à-dire tout ce qui se passe dans le puits, échappe à la vue des observateurs qui seraient à l’extérieur. La différence fondamentale avec les horizons habituels, c’est que ceux-ci sont relatifs à l’observateur. On est au centre, on a un horizon. Si l’on bouge, celui-ci se déplace avec nous. Il est relatif.

Et pas l’horizon des événements ?

Non, il est absolu. Il est quelque part défini dans l’espace-temps et quels que soient les observateurs, il est toujours là, il ne peut pas bouger.

Il faut donc se méfier des mots.

Oui, il faut faire attention aux mots communs qui sont utilisés à la fois en sciences et dans le langage courant. Cela induit souvent en erreur. Les célèbres philosophes français Gilles Deleuze et Félix Guattari ont dès la fin des années 80, en parlant des horizons, commencé à citer mes travaux sur les trous noirs. Mais ils parlaient d’horizons relatifs.

Justement, dans le langage courant, on utilise souvent le verbe aspirer pour les trous noirs. À bon escient ?

Il est pertinent dès que l’on met de la matière autour d’un trou noir déjà formé, qui va effectivement agir comme une sorte d’aspirateur gravitationnel. La matière autour, du gaz essentiellement, est progressivement capturée par le champ de gravité du trou noir et, en perdant progressivement de l’énergie, l’orbite se resserre et finit par disparaître dans le trou noir.

Cela a été observé ?

Oui, de façon indirecte, mais spectaculaire, avec des étoiles que l’on appelle les binaires X et qui orbitent autour de trous noirs. C’est d’ailleurs comme cela que l’on a découvert les premiers candidats à l’appellation de trou noir dans les années 1970.

Comment s’imaginait-on le processus avant cette observation ?

Des théoriciens en avance sur les possibilités instrumentales avaient imaginé un couple d’étoiles dans lequel une était normale, c’est-à-dire à l’état gazeux, et l’autre s’était transformée en trou noir. Le champ de gravité de celui-ci est tellement puissant qu’il arrache progressivement les couches extérieures de gaz de l’étoile partenaire.

Comment a-t-on ensuite observé cela ?

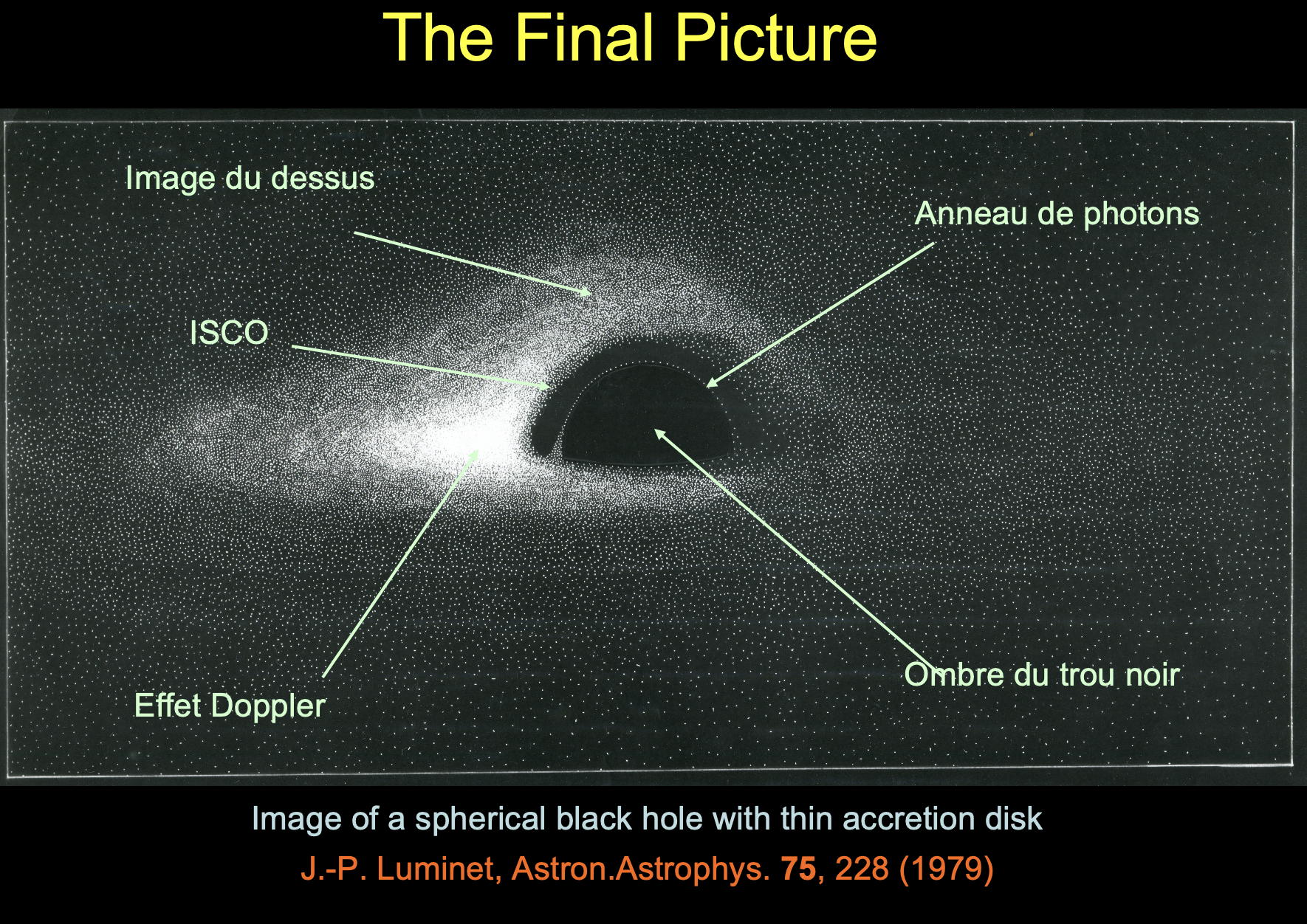
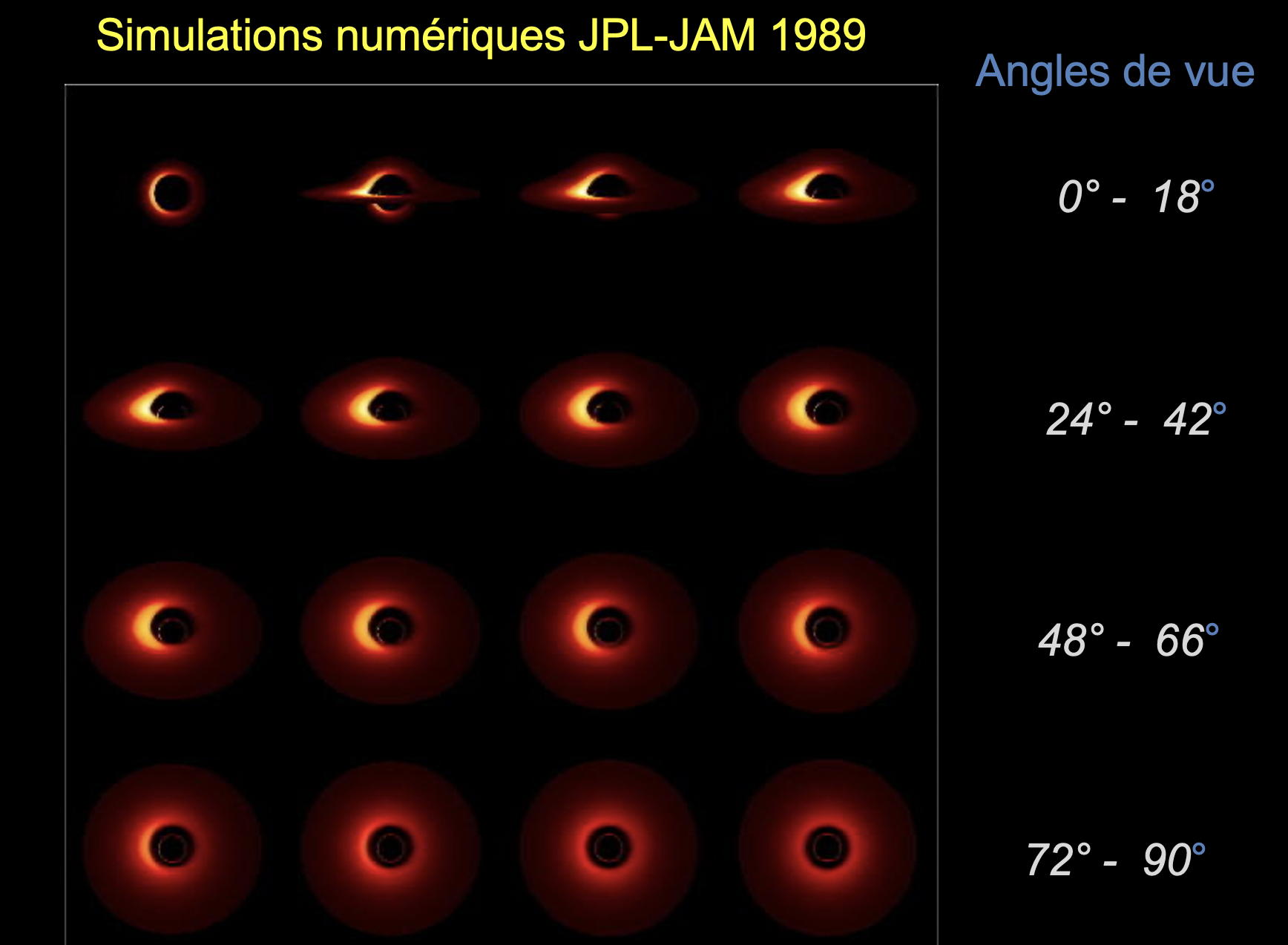
Indirectement par le fait qu’autour du trou noir, la matière arrachée à l’étoile partenaire forme ce qu’on appelle un disque d’accrétion qui tourne autour du trou noir, qui va progressivement spiraler vers l’intérieur en s’échauffant à des températures de plusieurs millions de degrés. Cela émet des rayonnements de très haute énergie qu’on appelle des rayons X.

C’est ce qui a fait que l’on a dû attendre pour les remarquer ?

Oui, c’est avec les années 1970 et les premiers télescopes à rayons X embarqués dans l’espace que cela a été rendu possible, puisque ceux-ci n’arrivent pas au sol, heureusement pour nous. Pour ce qui est de la représentation, nous avons des interprétations d’artistes où l’on voit effectivement une véritable aspiration des couches de l’étoile partenaire par le trou noir. Ces phénomènes se produisent extrêmement loin de la Terre, nous n’avons donc que des signatures indirectes à travers la distribution spectrale des rayons X.

Et est-ce que l’on sait ce qui arrive à la matière qui est aspirée ?

Non, c’est toute la question qui se pose, celle de savoir où va la matière et l’énergie qui sont aspirées. Nous n’avons aucune information. Ce qui se passe à l’intérieur ne peut pas être communiqué à l’extérieur. Le sort de la matière qui tombe dans un trou noir ne peut donc être décrit provisoirement que par des équations.

Qui nous disent quoi ?

Si l’on utilise les équations standards de la relativité générale, qu’on les extrapole jusqu’au bout, on aboutit à une absurdité physique qui serait un point singulier, c’est-à-dire un nœud de l’espace et du temps où tout devient infini. C’est ce caractère absurde qui a longtemps nui à la crédibilité des trous noirs dans le monde scientifique, y compris pour Albert Einstein.

Quand est-ce que cela a changé ?

Avec les travaux théoriques des années 1960-70, notamment ceux de Roger Penrose, Stephen Hawking et Brandon Carter, on découvre qu’avec les trous noirs en rotation, c’est un peu plus subtil que ça.

Dans quel sens ?

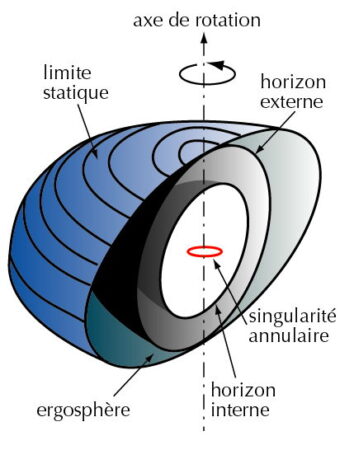
Il n’y a pas un nœud central, il y a un anneau et il y a des trajectoires théoriques qui peuvent éviter l’anneau et ne pas s’écraser indéfiniment, ce qui est un petit peu plus plausible. Mais surtout, on soupçonne, même si l’on n’a pas de bonne théorie complète actuellement, qu’à une certaine échelle, la théorie de la relativité générale cesse d’être valable, tout simplement parce qu’elle n’incorpore pas les effets de la physique quantique.

Qu’est-ce que cela implique ?

Dans les conditions d’effondrement gravitationnel, et la même question se posera pour le Big Bang, il y a un moment où la matière aspirée doit être soumise à des effets de physique quantique en s’approchant de ce qui pourrait être la singularité. La plupart des chercheurs qui travaillent sur ces questions-là estiment que des phénomènes quantiques vont éliminer la singularité en la remplaçant par divers processus.

Lesquels ?

Soit un rebond, c’est-à-dire qu’à une échelle très petite de taille, la gravité s’inverse, devient répulsive. Ça rebondit au lieu de s’écraser indéfiniment. Ou alors par des choses encore plus étonnantes et plus fascinantes dont on parle beaucoup, notamment dans la science-fiction, ces fameux trous de ver, c’est-à-dire ces passages, ces distorsions subtiles de l’espace-temps qui creuseraient des sortes de tunnels pour aller d’un point de l’univers à un autre.

À travers le trou noir ?

Oui, la bouche d’entrée, c’est lui. Et la sortie serait un trou blanc qui est inspiré de science-fiction, de Stargate jusqu’au film Interstellar, qui d’ailleurs fait l’objet de mon prochain livre qui s’intitule Voyager dans un trou noir avec Interstellar, où effectivement, je décode scène par scène tous les épisodes du film. Continuer la lecture de Des trous noirs à l’intelligence artificielle : la science ne dit pas tout sur le monde →

Astronomie, Histoire des sciences, Mes publications

Entretien sur la vie extraterrestre

février 8, 2025 Jean-Pierre LUMINET 3 commentaires

Je reproduis ci-dessous l’entretien paru dans l’ouvrage collectif “Contacts et OVNI : l’enquête” dirigé par François Deymier et Mathias Lebœuf (éditions Télémaque, 2025). J’y donne mes sentiments concernant les possibilités de vie extraterrestre – depuis les simples bactéries jusqu’aux plus improbables civilisations avancées, et l’interprétation du phénomène OVNI.
Je l’ai agrémenté de quelques illustrations.

*********************************************

Vous êtes astrophysicien mais aussi écrivain et poète, la question OVNI et/ou celle d’une vie extraterrestre font-elles partie du champ de vos préoccupations ?

Oui, et à divers titres ! Ces questions m’ont d’abord intéressé bien avant d’être astrophysicien, tout simplement parce que j’étais un grand lecteur de science-fiction quand j’étais adolescent. Vraiment ! J’ai lu des centaines de livres, tous les grands classiques du genre. Alors, forcément, la question de la vie extraterrestre m’intéressait – plus que celle des OVNIS, d’ailleurs, ceux-ci étant un cas très particulier de la vie extraterrestre. J’ai même écrit un roman de jeunesse de science-fiction, que je n’ai pas publié.

Quand je suis devenu ensuite astrophysicien, la question m’a intéressé dans le cadre de cette nouvelle discipline qui était en train de devenir scientifique : l’astrobiologie – on dit aussi exobiologie. Même si elle est en dehors de mon champ propre de recherche, elle fait désormais partie intégrante des sciences de l’univers. Il est donc difficile de ne pas s’intéresser à la possibilité d’une vie extraterrestre. Je parle ici de vie extraterrestre au sens le plus large du terme, les bactéries, j’y reviendrai.

Mais surtout, en tant que théoricien, la question des OVNIS m’a aussi interpelé parce que, si les OVNIS sont effectivement des vaisseaux extraterrestres, cela implique qu’il y a des civilisations très avancées qui nous visitent et qui ont donc découvert des lois physiques que nous ignorons ! C’est sur ce plan que le sujet m’intrigue : elles auraient découvert le moyen de voyager entre les étoiles, peut-être d’utiliser et de maîtriser certains phénomènes sur lesquels j’ai travaillé sur le plan théorique, comme les trous noirs et les trous de ver. C’est pour cette raison que le sujet fait partie de mes préoccupations. Le terme « préoccupation » est peut-être un peu fort, disons que cela fait partie de mes intérêts et de mes questionnements.

Vous avez écrit sur de nombreux astronomes du passé, certains d’entre eux croyaient-ils à une vie extraterrestre ?

Comme vous le savez, l’hypothèse de la pluralité des mondes habités avait déjà été avancée dans l’Antiquité, par les philosophes atomistes notamment comme Démocrite et Epicure. Elle a ensuite été interdite de pensée par l’Église, et commencé à revenir sur le devant de la scène à la fin du XVI^e siècle, avec Giordano Bruno (qui, rappelons-le, a été brûlé vif comme hérétique en 1600). C’est surtout à partir du XVII^e siècle, avec Galilée, Kepler et l’évolution de nos connaissances en astronomie, qu’on a commencé à comprendre que la physique d’ici-bas, la physique terrestre, est la même que la physique céleste. Et qu’en conséquence les autres planètes, contrairement à ce que pensait Aristote, pouvaient ressembler à la Terre. Est alors revenue l’idée d’autres mondes peuplés d’habitants. Parmi les auteurs sur lesquels j’ai écrit livres et articles, Kepler a publié à titre posthume un ouvrage étonnant intitulé Le Songe ou l’astronomie lunaire, dans lequel il imagine des habitants de la Lune, des « sélénites », en mesure d’observer le système solaire depuis notre satellite pour en découvrir les lois.

À partir de là, pendant deux siècles, quantité d’ouvrages ont été publiés sur la « pluralité des mondes habités », y compris par des auteurs très sérieux comme le physicien et astronome hollandais Huygens (qui a notamment découvert les anneaux de Saturne et inventé les horloges à pendule), ou encore le philosophe Kant qui, dans son Traité du Ciel, développe toute une théorie sur la possibilité de planètes du système solaire habitées, avec des êtres adaptés aux conditions complètement fantasmagoriques que l’on croyait alors y régner. L’un des plus fervents adeptes de la pluralité des mondes a été Camille Flammarion. Il faisait partie de ceux qui, à la fin du XIX^e siècle, croyaient notamment à l’hypothèse de canaux artificiels à la surface de Mars. Dans nombre de ses ouvrages, il fantasme sur les habitantes de Vénus à demi-nues se prélassant sous les tropiques, et autres savoureuses fantaisies…

Le paradoxe de Fermi est-il toujours intéressant ? valide ?

C’est une très bonne question soulevée en 1938 par le physicien prix Nobel de physique Enrico Fermi : « s’il y avait des civilisations extraterrestres, leurs représentants devraient être déjà chez nous. Où sont-ils donc ? ». En effet, à partir du moment où le Soleil est une étoile relativement jeune dans l’histoire de l’univers, il y a eu beaucoup d’autres étoiles qui se sont formées bien avant. Et si l’on croit que l’évolution naturelle conduit inéluctablement à l’émergence de formes vivantes de plus en plus sophistiquées, allant jusqu’à des civilisations technologiques, alors il devrait y avoir eu bien avant nous des civilisations beaucoup plus avancées que nous. Le raisonnement est donc le suivant : si ces civilisations développent les technologiques spatiales et découvrent la façon de voyager entre les étoiles, pourquoi ne nous ont-elles pas rendu visite de façon incontestable ?

Certains pensent qu’elles l’ont fait. Pour eux, la preuve en serait les pyramides d’Egypte ou d’autres constructions savantes, en Amérique du Sud et ailleurs… J’aimerais bien croire à tout cela, mais cela me paraît invraisemblable. Néanmoins le paradoxe de Fermi reste une très bonne question. Il y a plusieurs autres réponses, bien entendu ! Par exemple, une civilisation technologiquement avancée dans une galaxie donnée pourrait être très rare. Une autre réponse consiste en l’hypothèse qu’en fait les extraterrestres nous rendent visite mais qu’ils ne se manifestent pas, de sorte que l’on ne s’en rend pas compte… Le débat reste donc ouvert.

Justement, vous, à titre personnel, croyez-vous à une vie extraterrestre ? Si oui, pourquoi ?

Je dirais … plutôt oui. Mais essentiellement sous la forme la plus simple du vivant, c’est-à-dire la bactérie. Car je pense que l’évolution de l’arbre du vivant à partir d’une souche initiale, c’est-à-dire la bactérie, fondée sur des principes fondamentaux comme la chimie du carbone, dépend de facteurs endogènes très particuliers à l’histoire de chaque planète.

Donc, l’hypothèse de la vie extraterrestre, j’y crois plutôt, oui, même si le terme de « croire » n’est pas un terme que j’apprécie beaucoup dans la démarche scientifique. Disons que cela me semble plausible, au niveau basique, je le répète, des bactéries. Après, j’aimerais bien avoir des preuves indubitables et des confirmations qu’il existe ailleurs que sur Terre des formes de vie plus avancées que les bactéries. J’aimerais vraiment, pour les raisons que j’ai évoquées : des lois physiques inconnues, etc.

Dans la sphère scientifique, plus particulièrement dans le domaine de l’astrobiologie, le débat avance en ce moment dans deux directions opposées. On a deux écoles qui s’affrontent : l’école plutôt « classique », initiée par Carl Sagan, affirmant qu’il y a tellement de planètes dans l’univers qu’il n’est pas possible que la Terre soit la seule à accueillir le vivant. C’est un argument probabiliste, le problème est qu’il ne tient pas du tout la route, je vais vous dire pourquoi.

L’autre école fait l’hypothèse de la « terre rare », en mettant simplement en jeu une combinatoire, c’est-à-dire une combinaison d’un certain nombre de facteurs exceptionnels qui doivent s’enchaîner d’une certaine façon pour aboutir au vivant. Si l’on s’en tient à très peu de facteurs, par exemple juste du carbone, de l’eau liquide et de l’énergie, alors la vie apparaîtrait un peu partout, et je pense qu’on l’aurait déjà trouvée. Si par exemple on découvrait dans les années à venir des bactéries fossiles sur Mars, cela validerait la première hypothèse – et j’en serais personnellement ravi. Mais rien n’est certain ! De fait, les partisans de la vie « partout dans l’univers » invoquent un argument statistique qui ne résiste pas à l’analyse, tout simplement parce qu’on ne peut pas évaluer de probabilité d’occurrence de tel ou tel phénomène tant que l’on ne connaît pas l’ensemble des facteurs nécessaires à l’émergence du phénomène en question. C’est le cas pour le vivant. Les facteurs nécessaires sont très vraisemblablement en beaucoup plus grand nombre que trois ! Je me suis amusé à utiliser la combinatoire permettant de calculer la probabilité d’occurrence d’un phénomène donné – disons l’émergence d’une bactérie – à partir d’une bonne vingtaine de facteurs nécessaires, qui en outre doivent s’enchaîner d’une certaine manière ‑ à l’exemple de ce qui s’est probablement passé sur notre planète Terre. Le calcul fait intervenir des factorielles, et montre finalement que le nombre gigantesque de planètes que l’on suppose exister dans l’univers, de l’ordre de 10²¹, suffit à peine pour réaliser une occurrence ! L’hypothèse de la terre rare, si elle est philosophiquement un peu dérangeante, n’est donc pas absurde. Mon ami Jean-Pierre Bibring a récemment publié un livre fort intéressant[1] sur cette hypothèse. En poussant à l’extrême, la Terre pourrait être la seule planète de l’univers abritant de la vie, même au niveau aussi fondamental que la bactérie. Personnellement, je n’ai pas trop envie d’y croire, mais on ne peut pas éliminer cette hypothèse assez radicale. Continuer la lecture de Entretien sur la vie extraterrestre →

Arts visuels, Astronomie, Histoire des sciences

Observations Astronomiques : Huit toiles de Donato Creti (1711) décryptées

janvier 17, 2025 Jean-Pierre LUMINET 2 commentaires

Par une nuit radieuse et un ciel dégagé, imaginez-vous en pleine nature. Au-dessus de votre tête trône dans l’azur l’un de vos astres familiers – Lune, Vénus, Jupiter, Mars, etc. –, mais il est démesurément grossi par rapport à sa taille apparente réelle dans le ciel.

Non, vous n’êtes pas dans la célèbre Nuit étoilée peinte par Vincent van Gogh en 1889 à Saint-Rémy de Provence, mais dans l’une des huit étonnantes toiles astronomiques réalisées en 1711 par le peintre italien Donato Creti.

Né à Crémone en 1671, mort à Bologne en 1749, Creti a été principalement actif à Bologne. Cette belle ville italienne avait une grande tradition artistique, grâce notamment à l’Académie des Carrache et aux peintres baroques comme Guido Reni, Francesco Albani, ou Guercino (Le Guerchin).

Autoportrait de Donato Creti à l’âge de seize ans (1687)

Elève de Lorenzo Pasinelli, le jeune Donato a hérité du style bolonais caractérisé par une forte attention au dessin et à la clarté des formes, tout en développant sa propre manière. Son travail révèle ainsi un caractère plus doux et plus raffiné que celui des baroques typiques. Son style tend plus vers le classicisme, avec une utilisation subtile de la couleur et une attention aux détails. Ses compositions sont souvent gracieuses et pleines de sérénité, plutôt que dramatiques et émotionnelles comme celles de tant d’autres artistes baroques.

A l’instar de beaucoup de peintres de son temps, Creti a produit de nombreuses œuvres religieuses destinées aux églises et aux institutions religieuses de Bologne et de ses environs. Ces œuvres incluent des retables et des fresques. Son grand tableau pour l’église San Domenico de Bologne, montrant des scènes de la vie de San Vincenzo Ferreri (Saint Vincent Ferrier), est représentatif de son style classique et raffiné.

Saint Vincent Ferrier ressuscite un enfant – Eglise S. Domenico, Bologne (1732)

Creti a également peint des scènes mythologiques et allégoriques, marquées par une recherche de l’équilibre et de la beauté plutôt que par les mouvements exubérants typiques du baroque rococo. L’une de ses toiles de ce type les plus réputées est L’éducation d’Achille par le centaure Chiron. Cette quête inlassable et quasi maniaque d’une beauté idéale l’occupa toute sa vie, au point qu’il confessa dans ses écrits : « J’ai vécu pendant trente-six ans sans dormir, dans un état proche du délire, incapable de trouver, nuit comme jour, le moindre répit. »

Mais l’œuvre sans doute la plus originale de la carrière de Creti et qui fait l’objet de cet article est la série de huit toiles au format rigoureusement identique de 51×35 cm, datant de 1711 et intitulées Osservazioni Astronomiche (Observations astronomiques). Aujourd’hui conservée à la Pinacothèque du Vatican, la série fut commandée par le comte bolonais Luigi Marsili. Il demanda à l’artiste de peindre les astres du système solaire (Mercure, Vénus, Mars, Jupiter, Saturne, le Soleil, la Lune et une comète) revisités par les observations télescopiques de son temps. La commande n’était pas seulement de nature esthétique, son but réel était scientifique et diplomatique : suite aux premières observations à la lunette astronomique de Galilée (1610) et aux débats métaphysiques qui en découlaient, Marsili voulait attirer l’attention de l’Église sur la nécessité d’établir un observatoire astronomique au Vatican, en réponse à l’importance croissante que l’astronomie avait prise au XVII^e siècle – d’autant que la discipline était pratiquée par de nombreux Jésuites.

Tour de la Specola du Palazzo Poggi à Bologne

Le projet atteignit son but, puisque la Tour de la Specola du Palazzo Poggi de Bologne fut érigée à partir de 1712, sous le pontificat de Clément XI, pour y abriter le premier observatoire astronomique public d’Italie qui fut inauguré en 1726. Ce n’est qu’en 1787 que le collège romain se dotera de son propre observatoire au Vatican.

Chacune des huit toiles des Observations astronomiques s’attache à représenter l’une des cinq planètes du système solaire connues à l’époque, auxquelles sont ajoutées la Lune, le Soleil et une comète (la planète Uranus ne sera découverte au télescope qu’en 1781, et Neptune en 1846). Sur la scène terrestre des tableaux figurent des personnages en habits du XVIII^e siècle, installés dans des paysages souvent montagneux, parfois campagnards, pour observer le ciel.

Ces compositions sont dominées par la présence des astres fortement grossis par rapport à leur taille apparente réelle, agrémentés de certains détails perceptibles seulement aux télescopes de l’époque, dont la technologie venait d’être perfectionnée en Angleterre par Gregory et Newton et surpassait largement celle de la lunette de Galilée. Elles démontrent l’intérêt croissant pour l’astronomie au début du XVIII^e siècle, une époque marquée par des avancées scientifiques importantes, grâce notamment à des savants comme Galilée et Kepler.

Jacques de Lajoue : Allégorie de l’Astronomie, 1735, Huile sur toile, Musée de Cambrai

Dès lors les sciences sont venues s’immiscer dans le théâtre, la poésie et les arts visuels. Fontenelle venait par exemple d’écrire une pièce de théâtre, La Comète (1681), où il raillait les superstitions de l’astrologie. En peinture, le spectacle de la nature céleste a commencé à inspirer de nombreux artistes comme Jacques de Lajoue ou, en Angleterre, William Hogarth et Joseph Wright.

Bien qu’à ma connaissance Donato Creti n’ait fourni aucune indication sur ses sources d’inspiration scientifique, l’examen de l’iconographie astronomique de son temps m’a permis d’établir de vraisemblables correspondances, que j’expose ci-dessous toile après toile.

La Lune

Dans un paysage montagneux, deux personnages masculins sont installés sur une petite plateforme rocheuse pour observer la pleine Lune. L’un d’eux utilise une lunette très semblable à celle qu’avait employée Galilée tout juste un siècle auparavant. L’astre des nuits occupe une taille énorme dans le ciel et montre une surface tachetée. Continuer la lecture de Observations Astronomiques : Huit toiles de Donato Creti (1711) décryptées →

Astronomie, Histoire des sciences, Littérature

Tommaso Campanella, de l’Apologie de Galilée à la Cité du Soleil

mai 9, 2023 Jean-Pierre LUMINET 8 commentaires

Tommaso Campanella, philosophe italien né en 1568 en Calabre et mort à Paris en 1639, a passé pratiquement la moitié de sa vie dans diverses geôles de l’Inquisition. Opposé à Aristote et adepte d’une philosophie qualifiée de « naturaliste », il a été accusé d’hérésie à plusieurs reprises, mais sa désobéissance et ses récidives lui ont valu en 1602 une condamnation à trente années de prison. Il en effectuera vingt-sept, au cours desquelles il rédigera plusieurs ouvrages, dont L’Apologie de Galilée (1611) et La Cité du Soleil (1623), tout en correspondant avec de nombreux savants, dont l’humaniste provençal Nicolas Fabri de Peiresc. Ce dernier deviendra son ami lorsque, quittant enfin l’Italie en 1634, Campanella se réfugiera en France.

L’Apologie de Galilée est un traité répondant à la question que lui posa en 1611 le Saint Office au sujet de la thèse copernicienne défendue par Galilée : « Le Soleil est le centre du monde, la Terre n’est pas immobile, mais elle tourne autour d’elle-même et autour du Soleil ». Il peut paraître étrange que, sur un sujet aussi sulfureux, l’Église ait demandé consultation à un philosophe qu’elle avait elle-même emprisonné pour sa pensée hérétique ! Mais c’est un signe que, une année seulement après la publication du Sidereus Nuncius où les observations astronomiques rapportées par le savant italien réfutaient la théorie géocentrique de Ptolémée, l’Eglise cherchait des avis éclairés extérieurs à sa congrégation. En outre, Campanella avait connu Galilée à Padoue.

Ce petit traité représente un tour de force dans la mesure où il fut composé en très peu de temps par un homme qui n’avait d’autres ressources que sa prodigieuse mémoire et les innombrables lectures qu’il avait retenues. Sous une forme polémique très virulente, il est néanmoins très persuasif en raison de sa grande érudition. C’est un document historique qui révèle d’une part une dévotion de Campanella envers le savant Galilée plus qu’envers la vérité astronomique ou philosophique elle-même, d’autre part le courage qu’il y avait à risquer une aggravation des maux déjà supportés par le philosophe incarcéré.

L’Apologie de Galilée se termine par une péroraison demandant qu’on n’interdise pas au savant de poursuivre ses études et qu’on ne supprime pas ses écrits, ce qui, annonce-t-il, ferait tomber le ridicule sur les Saintes Écritures. Nous savons que cela n’a guère plaidé favorablement la cause de Galilée, qui sera lui-même condamné pour hérésie en 1633. Nous savons aussi que ce dernier s’est bien gardé de faire le moindre commentaire sur cet ouvrage apologétique, de même qu’il s’était bien gardé de faire la moindre allusion aux écrits de Giordano Bruno, petites lâchetés qui lui seront plus tard reprochées par Johannes Kepler. L’ouvrage ne sera publié en Italie qu’en 1621. Il faudra attendre 2001 pour disposer d’une remarquable traduction en français de Michel Lerner – spécialiste mondialement renommé de cette période charnière de l’histoire de l’astronomie, déjà auteur d’un Nicolas Copernic d’un Monde des Sphères –, accompagnée de 150 pages d’introduction et de 117 pages de notes de premier ordre. A cette époque je présidais la commission scientifique au Centre National du Livre et j’avais chaudement recommandé l’octroi d’une subvention pour l’édition de l’ouvrage !

Bien plus connue est La Cité du Soleil, utopie sociale et politique composée en latin, à l’exemple de la République de Platon et de l’Utopie de Thomas More (1516). Continuer la lecture de Tommaso Campanella, de l’Apologie de Galilée à la Cité du Soleil →

Mes publications, Sciences

Les Chroniques de l’espace illustrées (15) : Le mal de l’espace

janvier 12, 2023 Jean-Pierre LUMINET 2 commentaires

Ceci est la quinzième de mes « Chroniques de l’espace illustrées ». Si vous souhaitez acquérir mon livre dans sa version papier non illustrée (édition d’origine 2019 ou en poche 2020), ne vous privez pas !

Le mal de l’espace

En août 1961, les Soviétiques mettent en orbite Vostok 2 avec à bord le cosmonaute Guerman Titov, qui va pour la première fois passer une journée entière dans l’espace. Comme la cabine est grande, Titov se détache de son siège et flotte dans l’habitacle en l’absence de pesanteur. Ses mouvements deviennent soudain indécodables par son oreille interne, où se trouve le centre de l’équilibre, son cerveau ne sait plus interpréter sa position sans horizon visuel, les nausées l’envahissent. C’est le mal de l’espace, analogue au banal mal au cœur que nous ressentons en voiture sur une route montagneuse ou en bateau par mer agitée, mais bien plus violent.

Titov paraît sur l’écran de télévision du centre de contrôle au sol de la mission Vostok 2 juste après avoir atteint l’orbite nominale. Malgré le mal de l’espace il parviendra à manipuler un appareil photo pour prendre des clichés de la surface terrestre. caméra .

Iouri Gagarine, avec son court vol spatial, et les premiers Américains dans leurs très étroites cabines Mercury, n’avaient pas eu assez de temps ni d’espace pour éprouver ces malaises. Ces derniers vont désormais affecter plus ou moins fortement tous les astronautes, même si en général le cerveau s’adapte au bout de quelques jours.

Vue en coupe d’une cabine Mercury : le courageux astronaute est confiné dans une boîte de conserve.

Les problèmes vraiment sérieux apparaissent avec les premières missions de longue durée sur les stations orbitales, quand le mal de l’espace devient psychologique. L’organisation de la vie dans un milieu très confiné et inconfortable engendre en effet des conflits avec les contrôleurs au sol, le rejet de planifications excessives, une irritabilité entre les membres d’équipage, qui ne peuvent s’isoler, allant jusqu’à la dépression nerveuse.

C’est avec les stations russes que des progrès significatifs sont faits dans ce domaine. Le ravitaillement en orbite par des cargos automatiques, apportant une nourriture un peu plus soignée et présentable, de l’eau, du carburant, du courrier, des pièces détachées et permettant l’évacuation des déchets, rend possible d’augmenter la durée de vie en orbite de façon spectaculaire. La visite régulière d’équipages, en plus de celui qui est de permanence, contribue à garder un état psychologique plus équilibré. L’espace « linéaire » est démultiplié, les cosmonautes peuvent s’éloigner les uns des autres pour s’assurer un peu plus d’intimité. Progressivement, la durée des vols double et monte à six mois.

Un nouveau problème se présente alors : certains voyageurs de l’espace se retrouvent prostrés sous prétexte qu’il leur semble que la Terre les oublie. En outre, les phénomènes de décalcification osseuse et les atrophies musculaires engendrent des inadaptations à leur retour sur Terre. Pour y remédier, les stations orbitales sont dès lors équipées de salles de sport, où les cosmonautes suivent un entraînement physique constant. Continuer la lecture de Les Chroniques de l’espace illustrées (15) : Le mal de l’espace →

Actualités, Astronomie

Première image du trou noir galactique Sagittarius A*: un décryptage inédit

août 2, 2022 Jean-Pierre LUMINET 13 commentaires

Après cinq années de calculs et d’analyses, la collaboration internationale du télescope Event Horizon (EHT) a livré le 12 Mai 2022 l’image de Sagittarius A* (Sgr A*), le trou noir géant tapi au centre de notre galaxie (la Voie lactée), à 27 000 années-lumière de la Terre. Jusqu’à présent, on ne percevait qu’indirectement sa présence, à partir de quelques émissions dans le domaine radio et l’observation des trajectoires des étoiles orbitant à grande vitesse autour d’une masse gigantesque mais invisible. Après celle obtenue par l’EHT en 2019 du trou noir central de la lointaine galaxie M87, c’est donc la seconde image directe de ce type d’astre dont on dispose à ce jour.

Figure 1. Première image du trou noir géant Sagittarius A* situé au centre de la Voie lactée, dévoilée par les équipes du programme international de radioastronomie Event Horizon Telescope. © EHT Collaboration/ESO

Une recomposition complexe

Souvenez-vous. La toute première image télescopique d’un trou noir entouré d’un disque de gaz chaud avait été dévoilée en avril 2019 par les mêmes équipes de l’EHT : il s’agissait du trou noir M87* situé au centre de la galaxie elliptique géante M87, distante de 56 millions d’années-lumière. Les observations de Sgr A* avaient été effectuées en avril 2017, lors de la même campagne que celles de de M87*. S’il a fallu cinq années d’analyse pour Sgr A* contre deux pour M87*, c’est parce que durant le temps de pose des observations – de l’ordre de l’heure – , l’émission lumineuse du disque de gaz autour de Sgr A* est très variable, alors que celle autour de M87* est figée. La raison tient à ce que Sgr A* a une masse 1500 fois plus faible que M87* (4 millions de masses solaires pour SgrA* contre 6 milliards pour M87*), de sorte que l’échelle de temps caractéristique de la variabilité lumineuse, donnée par la simple formule GM/c³, est beaucoup plus rapide : 20 secondes, contre plusieurs heures pour M87*.

Figures 2a-b. En haut, le montage illustre l’énorme différence de tailles entre M87* et SgrA*, rapportées à la taille de notre système solaire. En bas :en raison de sa taille géante, la structure lumineuse autour de M87* a très peu varié au cours des 4 jours d’observations effectuées en avril 2017.

Tenter de capturer une image nette de SgrA* dans un temps de pose d’une heure revenait donc à prendre la photo d’un chien courant après sa queue. Il a fallu un travail d’intégration considérable pour reconstruire une image “moyenne” de SgrA* suffisamment nette, comme le montre clairement la figure 3.

Figures 3a-b. A gauche, plusieurs dizaines de clichés de SgrA* montrent sa grande variabilité temporelle, au point que la reconstruction d’une image moyennée ne peut reproduire précisément l’état du flot d’accrétion (position incertaine des surbrillances). A droite en revanche, pour M87*, en raison de sa taille géante, la structure lumineuse qui l’entoure a très peu varié au cours des 4 jours d’observations effectuées en avril 2017, de sorte que l’image moyenne reflète assez fidèlement l’état réel du flot d’accrétion.

Pour atteindre la résolution angulaire nécessaire pour imager SgrA* et M87*, équivalente à l’angle minuscule sous lequel nous verrions depuis la Terre une pomme sur la Lune, l’EHT a utilisé un réseau de radiotélescopes s’étendant de l’Antarctique à l’Amérique du Nord en passant par le Chili, les îles Hawaï et l’Europe de façon à avoir l’équivalent d’un instrument unique de taille planétaire, fonctionnant en mode interférométrique.

Figure 4. Les huit radiotélescopes du réseau EHT utilisés en avril 2017

Ce qui frappe de prime abord, c’est que les deux photographies de M87* et de SgrA* se ressemblent beaucoup : au centre, une ombre noire, image de l’horizon des événements (nom donné, je le rappelle, à la surface intangible d’un trou noir) agrandie d’un facteur 2,6 – (comme je l’avais montré dans mon article de 1979, cf. fig. 5), entourée d’une couronne lumineuse jaune-orangée, floue et présentant des taches de surbrillance.

Figure 5. Schémas extraits de mon article de 1979 et de mon ouvrage de vulgarisation “Le destin de l’univers” (2006), illustrant comment “l’ombre” d’un trou noir est l’image agrandie de son horizon des événements d’un facteur 2,6, en raison d’un effet de lentille gravitationnelle. Un anneau de lumière très fin, appelé anneau de photons, l’encercle.

Figure 6. Les deux images télescopiques ressemblantes de M87* et SgrA*

La différence la plus importante est l’apparence de trois taches surbrillantes bien distinctes dans l’anneau lumineux de SgrA*, alors que l’anneau de M87 est continu avec deux zones de surbrillance contigues. De même, l’ombre centrale paraît moins ronde pour SgrA*, sans doute en raison du grand nombre d’images qu’il a fallu intégrer pendant les heures d’observations.

Un catalogue de plusieurs milliers de simulations numériques a été établi aux fins de comparaison avec les clichés de l’EHT et de fixer des plages de valeurs probables pour les caractéristiques physiques (angle de vue, spin, etc) de SgrA*. Du gaz chaud ionisé tourne rapidement autour du trou noir, formant comme des bras spiraux qui deviennent plus brillants à leur tangence avec l’anneau de photons, où la lumière est amplifiée par lentille gravitationnelle forte. Ce sont ces points brillants qui sont intégrés au cours du temps, et qui donnent la structure générale des couronnes lumineuses.

Figure 7. Il a fallu effectuer des milliers de simulations numériques pour reconstruire une image nette de SgrA*

Disque d’accrétion ou anneau de photons?

Que révèlent au juste ces deux clichés historiques ? A première vue (vue réservée cependant à quelques connaisseurs) on est tenté de les comparer avec les simulations numériques effectuées en 1979 par moi-même et en 1989 avec mon collaborateur Jean-Alain Marck:

Figure 8. Première simulation numérique d’un trou trou noir entouré d’un disque d’accrétion, parue en janvier 1979, avec légendes ajoutées. L’ombre du trou noir est au centre. “L’image du dessus” est l’image directe (dite) primaire du disque d’accrétion, déformée cependant par le champ de gravité. L’ISCO (Inner Stable Circular Orbit) est la dernière orbite stable marquant le bord interne du disque d’accrétion. L’anneau lumineux qui entoure l’ombre est la superposition de l’anneau de photons et des images secondaire, tertiaire, etc. du disque d’accrétion. L’effet Doppler dû au mouvement du gaz à vitesse relativiste explique la forte asymétrie du flux lumineux apparent vu à grande distance. Le flux lumineux calculé est cependant “bolométrique”, c’est-à-dire intégré sur toutes les longueurs d’onde du rayonnement électromagnétique.

Figure 9. Simulations numériques effectuées avec Jean-Alain Marck en 1989, reprenant mes calculs de 1979 mais y ajoutant de fausses couleurs et des angles de vue variables, grâce aux progrès des ordinateurs de l’époque.

d’en relever les frappantes similitudes :

Figure 10. Ressemblances à première vue frappantes entre les images télescopiques (en haut) et les simulations numériques (en bas)

et d’en tirer des conclusions rapides concernant la structure du disque d’accrétion et l’angle sous lequel il est vu depuis la Terre:

Figure 11. Une interprétation à première vue tentante…

J’avoue m’être moi-même laissé entraîner par cette interprétation, qui d’une part flattait mes calculs pionniers, d’autre part n’était aucunement démentie par les chercheurs de l’EHT, qui m’ont au contraire déroulé un tapis rouge lors de la première conférence tenue sur le sujet à l’Université de Harvard en juin 2019.

Figure 12. Ma conférence de clôture de la Black Hole Initiative Conference tenue à l’Université de Harvard les 20-22 mai 2019 après la publication de la première image télescopique de M87*.

Au point que, tant pour l’image de M87* que pour celle plus récente de SgrA*, cette interprétation a été reprise dans la plupart des médias de vulgarisation scientifique. D’autant que les articles spécialisés publiés par les chercheurs de l’EHT, bourrés de détails techniques, restent étrangement vagues sur la question…

Or, la réalité physique est toujours plus complexe que nos premières grilles de lecture. Une analyse plus fine, faite depuis 2019 sur M87* et renforcée en 2022 par celle de SgrA*, suggère que la couronne lumineuse en forme de « donut » n’est pas l’image directe des disques d’accrétion gazeux orbitant autour de leurs trous noirs respectifs, et que les surbrillances ne reflètent pas complètement l’état réel du gaz autour du trou noir, ni ne traduisent l’effet Doppler dû à la rotation relativiste du gaz ! Continuer la lecture de Première image du trou noir galactique Sagittarius A*: un décryptage inédit →

Histoire des sciences, Mes publications, Sciences

Les Chroniques de l’espace illustrées (14) : La navette spatiale

juillet 29, 2022 Jean-Pierre LUMINET Un commentaire

Ceci est la quatorzième de mes « Chroniques de l’espace illustrées ». Si vous souhaitez acquérir mon livre dans sa version papier non illustrée (édition d’origine 2019 ou en poche 2020), ne vous privez pas !

La navette spatiale

Début 1969, en pleine euphorie de la réussite des missions lunaires, la Nasa étudie la suite à donner au programme Apollo. Plusieurs propositions sont élaborées en interne : station spatiale, base lunaire, expédition vers Mars, navette spatiale. Mais la guerre du Vietnam pèse lourdement sur les budgets. La Nasa est consciente de la nécessité de baisser les coûts. Jusqu’à présent, les fusées, capsules et vaisseaux n’étaient prévus que pour une unique utilisation. L’agence américaine persuade le Congrès, dispensateur de crédits, qu’un véhicule spatial réutilisable va faire tomber le prix des lancements de fusées et stopper les ambitions des rivaux européens et soviétiques.

C’est ainsi que naît la navette spatiale, véritable chef-d’œuvre de technologie fondé sur un modèle d’avion classique avec ailes delta à profil évolutif.

Premières esquisses de la navette spatiale américaine (NASA, années 1960)

Le décollage de la première navette Columbia, le 12 avril 1981, est un grand moment télévisuel. La puissance des boosters à la mise à feu est impressionnante. Après quelques manœuvres en orbite, l’avion-fusée atterrit deux jours plus tard sur une base aérienne. Pour la première fois, un équipage revient de l’espace et se pose de la même manière qu’un avion sur une piste. C’est un succès, malgré le grand nombre de tuiles de la protection thermique endommagées.

Décollage historique de la navette Columbia le 12 avril 1981

A gauche, les astronautes John Young et Robert Crippen dans le poste de pilotage de Columbia lors de son premier vol. A droite, retour sur Terre après le vol inaugural. © Nasa

Cinq modèles de navettes seront fabriqués et voleront entre 1981 et 2011 : Columbia, Discovery, Challenger, Atlantis et Endeavour.

À leurs débuts, leur mission consiste essentiellement à lancer des satellites commerciaux civils et surtout militaires. Elles placent aussi en orbite haute d’importants télescopes spatiaux, comme le fameux Hubble Space Telescope et le satellite à rayons X Chandra.

La navette Discovery, décolle du Centre spatial Kennedy le 24 avril 1990, emportant dans sa soute le télescope spatial Hubble.

Continuer la lecture de Les Chroniques de l’espace illustrées (14) : La navette spatiale →

Arts visuels, Astronomie, Histoire des sciences

L’étoile de la Nativité : légende mystique, conjonction planétaire ou comète ? (2/2)

janvier 8, 2022 Jean-Pierre LUMINET 27 commentaires

Suite du billet précédent

Dans cette célèbre fresque de l’Adoration des Mages, réalisée par Giotto di Bondone en 1303, l’étoile de la Nativité est représentée sous forme d’un astre chevelu, autrement dit une comète. Nombre d’historiens estiment qu’il s’agit probablement d’une fidèle reproduction de la brillante comète vue en 1301 dans les cieux d’Europe, comète qui sera plus tard identifiée comme étant la comète périodique de Halley.

En 1979, un article de l’historienne de l’art américaine Roberta Olson [1] affirmait que l’étoile de la Nativité, peinte par Giotto dans l’Adoration des Mages du cycle de fresques de la chapelle Scrovegni à Padoue, représente la comète de Halley. Le cycle, commandé par le marchand Enrico degli Scrovegni, a été commencé en 1303 et l’Adoration des Mages date probablement de la même année ou de l’année suivante.

Ce livre richement illustré sur les météores et les comètes, que je possède dans ma bibliothèque, reprend les thèses de l’article de Roberta Olson.

Or, la comète qui portera bien plus tard le nom d’Edmund Halley après que celui-ci ait montré qu’elle revenait périodiquement tous les 76 ans dans les parages du Soleil et correctement prédit son prochain retour pour 1748, était précisément passée en 1301 et avait illuminé le ciel nocturne de tout l’hémisphère nord, comme l’attestent les annales d’astronomie chinoise.

Olson pense que le peintre en a été tellement impressionné qu’il en a dessiné une représentation résolument naturaliste, un astre bien concret et chevelu, c’est-dire une comète. C’est une première dans l’histoire de l’art. Bien qu’une partie importante de la tradition religieuse de l’époque associait effectivement l’étoile de Bethléem à une comète, la tradition iconographique se limitait à la représenter comme une petite étoile stylisée, souvent avec des rayons de lumière éclairant le nouveau-né divin.

Deux représentations artistiques médiévales de l’Adoration des Mages avec l’étoile symbolique de la Nativité. A gauche, Codex de Bruchsal, 1220. A droite, Les Riches Heures du Duc de Berry, 1411-1416.

Cette représentation plus tardive de l’étoile de la Nativité suggérant un noyau de comète prolongé par une queue se trouve dans le très bel ouvrage du Polonais Stanislaw Lubienetski, “Theatrum Cometicum”, publié en 1668.

Dans le chef-d’œuvre de Giotto, la comète, grande et étincelante, domine le ciel de la fresque. Sa voûte vibre d’énergie ; en son centre se trouve l’astre chevelu, exhibant un centre lumineux de condensation et une queue rayée donnant un sens dynamique à l’arc tracé par la comète dans sa trajectoire céleste. C’est ainsi que les comètes les plus spectaculaires apparaissent à l’œil nu, et c’est ainsi que la comète « de Halley » a pu se montrer au peintre.

Selon certains auteurs, Giotto aurait reproduit fidèlement le centre brillant de la tête de la comète sous la forme conventionnelle d’une étoile à huit branches, pour donner l’illusion de translucence, comme dans la nature.

La comète de Halley est la plus célèbre des comètes périodiques, revenant dans les parages du Soleil et de la Terre tous les 76 ans, le temps d’une vie humaine. La plus ancienne mention de son observation remonte à l’an 611 avant notre ère, en Chine, dans les Annales des Printemps et Automnes. Son passage en l’an – 164 a également été consigné dans une tablette d’argile babylonienne – voir l’article de Wikipedia pour plus de précisions.

Compte-rendu Chinois de l’apparition de la comète de Halley en 240 av. J.-C., extrait des Annales Shiji_(史記)

Son plus récent passage, en 1986, offrait un spectacle visuel peu spectaculaire car la comète se trouvait alors à l’opposé du Soleil par rapport à la Terre, et n’était à peine visible à l’œil nu que depuis l’hémisphère sud. Mais, quittant notre planète, une flotte de cinq sondes spatiales s’est lancée à sa rencontre – deux Soviétiques, deux Japonaises, et une Européenne. Cette dernière fut judicieusement baptisée Giotto en hommage au peintre italien – preuve, s’il en fallait une, que tous les astronomes ne sont pas dépourvus de culture historique et artistique.

Vue d’artiste de la sonde européenne Giotto lancée en 1986.

Après un trajet de 150 millions de km parcourus en 8 mois, la sonde s’approche à 600 km du noyau cométaire pour en déterminer la taille et la forme – une sorte de cacahuète sombre – et sa nature physique. Et elle prend ce film extraordinaire où l’on voit lentement avancer un rocher irrégulier de 16 km de long sur 8 km de large. Mais derrière les images apparemment sereines, les astronomes devinent une surface criblée de geysers, des poches de glace congelée qui se vaporisent et jaillissent de tous côtés à mesure que le noyau se rapproche du soleil…

Toujours est-il que la comparaison entre l’astre chevelu peint par Giotto en 1303 et la photographie prise « de près » par la sonde éponyme est spectaculaire : même structure, même rapport entre la taille de la tête et le développement de la queue…

Toutes les missions astronomiques consacrées au passage de Halley/1986 n’ont pas été aussi heureuses. Ainsi, la navette spatiale Challenger s’était envolée le 28 janvier 1986 avec dans l’équipage une jeune institutrice censée donner des cours en direct depuis l’espace sur la comète. On se souvient que l’explosion de la navette pendant le décollage avait tué les sept membres de l’équipage.

***

Outre que très séduisante, l’hypothèse d’Olson paraît convaincante. Mais, aussi bien en science fondamentale qu’en histoire des sciences, cela vaut toujours la peine de creuser davantage, et il est légitime de se poser les deux questions suivantes :

1/ L’astre représenté par Giotto a-t-il vraiment été la comète de Halley passée en 1301 ?

2/ Et, pour en revenir au sujet de fond de ces billets de blog, l’étoile de la Nativité qui a guidé les rois Mages a-t-elle vraiment été une comète ?

L’étude d’Olson a été approfondie par l’astronome et vulgarisateur italien Paolo Maffei dans une magistrale fresque historique sur la comète de Halley [2]. Selon lui, l’attribution pose des problèmes car, alors que la comète peinte par Giotto est rouge, celle de Halley en 1301 était blanche, du moins selon les chroniques chinoises. De plus, une autre comète est apparue en 1301, qui a été vue en décembre et janvier, c’est-à-dire juste autour des festivités liées à la fresque en question (alors que celle de Halley était visible entre mi-septembre et fin octobre). Maffei estime probable que Giotto ait confondu les deux comètes dans son souvenir, les prenant pour une seule, et il cite le chroniqueur Giovanni Villani, qui parle en fait d’une seule apparition cométaire qui a duré de septembre à janvier. Maffei examine également les descriptions d’apparitions d’autres comètes entre 1293 et 1313 et en conclut qu’elles étaient soit imaginaires, soit trop discrètes pour avoir servi de “modèle” à la représentation de Giotto.

Dans une étude de 1999, Gabriele Vanin, astronome amateur italien et président de l’Unione Astrofili Italiani (qui, entre parenthèses, m’a attribué en 2008 son prix international « Lacchini »), ajoute quelques critiques d’ordre strictement astronomique à l’hypothèse d’Olson ainsi qu’à certaines conclusions de Maffei. Tout d’abord, la comète de Halley était-elle vraiment “grande et brillante” lors de son passage de 1301 ? Selon le catalogue de Ho Peng Yoke, qui compile d’anciennes observations chinoises, japonaises et coréennes [3], la queue de la comète atteignait une longueur maximale de dix pieds chinois, soit environ 15°. Quant à la brillance de la couronne de la comète, il n’existe pratiquement aucune estimation dans les sources orientales. L’hypothèse de Maffei selon laquelle la phrase, rapportée par Ho, “atteignant la grande étoile de Nan-Ho [Raccoon]” signifie que Halley a égalé Raccoon (magnitude 0,34) en brillance, n’est pas convaincante, car l’attribution concerne le déplacement dans le ciel de la comète, apparue initialement dans la partie sud des Gémeaux (Tung-Ching). Très approximativement, en tenant compte de la distance minimale de la Terre atteinte lors de ce passage (0,18 unité astronomique, soit 27 millions de kilomètres), et du fait qu’elle ait été observée en septembre 1301 environ un mois avant son périhélie, supposant en outre que les paramètres photométriques étaient similaires aux paramètres actuels, on peut estimer que la comète a atteint une magnitude comprise entre 1 et 2, ce qui ne l’a pas rendu plus éclatante que les dizaines d’étoiles d’éclat comparable.

Dans ces conditions il est très difficile d’observer le noyau de la comète à l’œil nu aussi clairement que Giotto le représente, même dans le cas de grandes comètes passant près de la Terre, comme ce fut le cas des spectaculaires apparitions des comètes Hyakutake en 1996 et Hale-Bopp en 1997, auxquelles j’avais à l’époque consacrées des documentaires de télévision.

On peut se demander combien de grandes comètes la critique d’art Roberta Olson avait personnellement vues pour croire avec une si grande certitude qu’elles ressemblent à la représentation de Giotto. Il est certain que Hyakutake et Hale-Bopp ne correspondaient guère au paradigme de Giotto, avec leur énorme tête et leurs queues qui commençaient larges et s’effilaient progressivement. Même les autres grandes comètes qu’Olson aurait pu observer personnellement entre les années 1950 et 1970, comme Arend-Roland, Seki-Lines, Ikeya-Seki, Bennett et West, ne s’apparentaient pas à la comète de Giotto.

Les spectaculaires comètes Yakutake (à gauche) et Hale-Bopp (à droite) observées respectivement en 1996 et 1997.

Quant à la seconde comète de 1301, même si elle a réellement existé , elle a dû être beaucoup moins voyante que celle de Halley, si l’on considère que les très complètes chroniques orientales ne la recensent même pas (seul l’astronome français Alexandre-Guy Pingré (1791-1796) la mentionne, et en citant des observations exclusivement européennes, sachant à quel point les descriptions médiévales des phénomènes célestes étaient peu fiables).

Ces doutes astronomiques sont renforcés par des considérations purement artistiques. Dès 1985, un court mais incisif essai de Claudio Bellinati [4] démontait littéralement l’interprétation iconographique d’Olson. Son auteur soutient que la représentation “naturaliste” de la comète est un fait typiquement padouan, car elle n’est pas répétée dans trois autres représentations plus tardives (de Giotto ou de son école) de l’histoire de l’enfance du Christ (basilique inférieure d’Assise, 1315-16) et de l’Adoration des Mages (1320, Metropolitan Museum de New York), où l’étoile de la Nativité a des formes stylisées.

Scène de la Nativité du Christ de Giotto dans la Basilique inférieure d’Assise

Giotto di Bondone, Adoration des Mages, 1320 (Metropolitan Museum, New York)

La représentation padouane n’aurait donc pas été influencée par une vision directe de la comète de Halley ou de toute autre comète apparue dans ces années-là, mais par la lecture de l’Evangile du Pseudo-Matthieu et l’inspiration provenant de Pietro D’Abano et des maîtres physiciens de la cathédrale de Padoue. Continuer la lecture de L’étoile de la Nativité : légende mystique, conjonction planétaire ou comète ? (2/2) →

Astronomie, Histoire des sciences, Littérature

L’étoile de la Nativité : légende mystique, conjonction planétaire ou comète ? (1/2)

janvier 6, 2022 Jean-Pierre LUMINET 5 commentaires

Comme vous le savez, l’étoile de Bethléem, ou étoile de la Nativité, est le signe qui, dans la tradition chrétienne, a annoncé à des mages orientaux la naissance de Jésus et les a guidés vers Bethléem pour rendre hommage au Messie annoncé par les Prophéties. L’Epiphanie, le 6 janvier, célèbre précisément le jour de l’Adoration des Mages, scène réelle ou fictive qui a au moins l’immense mérite d’avoir suscité de nombreux chefs-d’œuvre de l’histoire de l’art. Notons cependant que, sur les quatre évangiles dit canoniques, seul celui de Matthieu (chap. II, versets 1-10) évoque l’étoile et la visite des Mages.

Évangile selon Matthieu, Codex Harleianus 9, minuscule 447 (Gregory-Aland), XVe siècle, British Library.

La nature de l’étoile de la Nativité a fait l’objet d’innombrables spéculations au cours des siècles. Les propositions d’explications vont du pur miracle à la fable pieuse, en passant par les tentatives de conférer une base rationnelle au récit de Mathieu par le biais d’un événement astronomique réel. Vous ne serez pas étonné si je m’en tiens ici aux hypothèses astronomiques, malgré une petite surprise que je vous réserve pour la toute fin… Compte tenu de l’ampleur du sujet et de la riche iconographie, je sépare cet article en deux billets distincts. J’y fais un résumé de plusieurs de mes textes disséminés çà et là dans mes écrits passés, fondés comme toujours sur une documentation rigoureuse et des recherches effectuées par quelques éminents collègues en histoire des sciences.

Il y a essentiellement trois sortes d’événements célestes suffisamment spectaculaires pour faire office de candidats :

une conjonction exceptionnelle de planètes,
l’arrivée d’une comète brillante,
l’apparition d’une étoile nouvelle (fin explosive d’une étoile en nova ou supernova)

Lire l’excellent et très documenté ouvrage de mon collègue et ami Jean-Marc Bonnet-Bidaud sur 4000 ans d’astronomie chinoise.

Eliminons d’emblée la troisième hypothèse, malgré quelques articles ayant tenté de la soutenir. Les « étoiles nouvelles », dont l’éclat peut en effet augmenter au point de devenir visibles à l’œil nu durant quelques jours, quelques semaines ou quelques mois, ont été soigneusement consignées durant plus de deux millénaires dans les annales d’astronomie d’Extrême-Orient (Chine, Corée, Japon). Or, aucune mention d’une telle apparition durant la période supposée de la naissance de Jésus ne ressort de la compilation de ces annales.

Consacrons donc ce premier billet à l’hypothèse d’une rare conjonction planétaire. C’est ma préférée pour la bonne (et très subjective !) raison qu’elle a été avancée pour la première fois par mon astronome préféré : le génial Johannes Kepler, auquel j’ai consacré deux romans historiques et maints articles ! Elle a aussi l’avantage d’être associée de curieuse manière à l’apparition d’une étoile nouvelle survenue un an plus tard.

Les paragraphes qui suivent sont développés dans ce roman publié en 2009, troisième volume de ma série des “Bâtisseurs du Ciel”. Disponible également en Livre de poche.

Nous sommes en 1604. Depuis la mort de Tycho Brahe trois années auparavant, Johann Kepler a pris sa succession comme mathématicien et astrologue impérial auprès de Rodolphe II de Habsbourg, à Prague. Il travaille d’arrache-pied sur les données de son défunt maître pour accoucher les lois des mouvement planétaires, qu’il ne finalisera que des années plus tard dans son Astronomia Nova puis son Harmonices Mundi.

La Nova Stella de 1604 représentée dans l’Epitomé de l’Astronomie Copernicienne publiée par Kepler entre 1618 et 1621

C’est alors qu’à l’automne une étoile nouvelle, une «Nova Stella » selon la terminologie de l’époque, surgit dans la constellation d’Ophiucus, à l’époque nommée Serpentaire. Elle va rester visible à l’œil nu près d’une année, si bien que des dizaines d’astronomes à travers l’Europe peuvent suivre son évolution.

Mais, de par sa position auprès de l’empereur, Kepler est le plus sollicité de tous. De toutes les universités du vieux monde on lui écrit pour lui faire part de ses propres observations et de ses interprétations. On vient le voir, on le questionne, on est inquiet. Les demandes les plus pressantes viennent du palais impérial : la cour l’accable de demandes d’horoscopes personnels, de prédictions sur le destin des royaumes et de l’empire. Tous veulent connaître la traduction de ce message divin, qui semble vouloir s’inscrire dans un contexte bien particulier. Un an plus tôt en effet, en 1603, a eu lieu dans le ciel une conjonction planétaire exceptionnellement rare entre Jupiter, Saturne et Mars. Ce « trigone flamboyant » avait déjà suscité toutes sortes de prédictions, telles que la conversion des Indiens d’Amérique, une émigration généralisée vers le Nouveau Monde, la chute de l’Islam ou encore et comme toujours dans ces cas-là, le retour du Christ… Continuer la lecture de L’étoile de la Nativité : légende mystique, conjonction planétaire ou comète ? (1/2) →

Astronomie, Histoire des sciences

La constellation d’Orion, ou la Main montée au ciel

décembre 12, 2021 Jean-Pierre LUMINET 5 commentaires

« Mais je reviens à ma journée du Dimanche. C’était avec plaisir que je voyais Papa venir nous chercher. En revenant je regardais les étoiles qui scintillaient doucement et cette vue me ravissait… Il y avait surtout un groupe de perles d’or que je remarquais avec joie trouvant qu’il avait la forme d’un T (voici à peu près sa forme), je le faisais voir à Papa en lui disant que mon nom était écrit dans le Ciel et puis ne voulant rien voir de la vilaine terre, je lui demandais de me conduire ; alors sans regarder où je posais les pieds, je mettais ma petite tête bien en l’air, ne me lassant pas de contempler l’azur étoilé ! »

Thérèse de Lisieux, Manuscrit A, folio 17/18

Extrait d’une lettre manuscrite de Thérèse dessinant le « T » formé par les étoiles du Baudrier (barre horizontale) et celle de l’Epée (barre verticale)

La constellation d’Orion pris par le Télescope spatial Hubble (les lignes caractéristiques joignant les étoiles sont rajoutées au cliché)

Orion est pour beaucoup la plus belle constellation du ciel. Visible l’hiver sous les latitudes européennes, la figure du géant Orion se dessine par neuf étoiles principales : quatre (dont Bételgeuse et Rigel sont de première grandeur) forment un rectangle et trois sont alignées dans le Baudrier, appelées aussi les Trois Rois. Chez les Égyptiens, Orion était identifié au dieu Osiris, dieu de la Mort et de l’outre-monde : son sarcophage du dieu, figuré par les trois étoiles alignées au centre, formant le Baudrier, était veillé par les quatre fils d’Horus, symbolisés par Saïph, Bételgeuse, Bellatrix et Rigel.

Dans la mythologie grecque, le chasseur géant Orion poursuit les Pléiades, tenant de la main gauche une peau de bête ou un bouclier, brandissant de l’autre une massue ou une épée pour combattre le Taureau qui se précipite sur lui. Orion est donc un thème de choix pour les cartographes du ciel.

On pourrait écrire pour le moins un livre entier sur les mythes et légendes du monde entier liés à cette configuration stellaire exceptionnelle, et plus encore sur la richesse d’informations astronomiques que l’on tire de son observation et de son étude. On se contentera ici de quelques aperçus.

Le chasseur Orion combattant le Taureau (Atlas de Fortin, 1776)

Le premier recensement scientifique connu des étoiles d’Orion figure dans L’Almageste de l’astronome grec d’Alexandrie Claude Ptolémée (vers 150 ap. J.-C.). La première ligne désigne non pas une étoile mais une nébuleuse. La deuxième décrit Bételgeuse, donne sa longitude et sa latitude, et lui assigne une magnitude de 1. Dans la dernière colonne, Ptolémée assigne en effet une grandeur aux étoiles, le nombre 1 étant attribué à la plus brillante et 6 à la plus faible. L’autre étoile de première grandeur, qui sera ultérieurement connue sous le nom de Rigel, est décrite quelques lignes plus bas comme « l’étoile brillante qui est dans le pied gauche en contact avec l’eau ».

Suite à l’acquisition d’un manuscrit d’Aratus datant du ixe siècle dans la version de Germanicus, aujourd’hui conservé à la Reijksuniversitet de Leyde, Hugo de Groote, dit Grotius (1583-1645) entreprit une belle édition des Phénomènes d’Aratus qui vit le jour en 1600. Les illustrations représentent le chasseur Orion de dos, le bras gauche couvert d’une peau de lion. Les étoiles qui courent le long de sa colonne vertébrale sont une pure invention du graveur. Dans Hyginus, Poeticon astronomicon (Venise, 1482), la gravure représente Orion vu de face, armé d’un bouclier et d’une massue. Bien que les positions des étoiles soient indiquées, elles ont peu de rapport avec les positions décrites par Hyginus, et encore moins avec la réalité.

A gauche, Orion vu de dos, dans Grotius (1600). A droite, Orion vu de face, dans Hyginus (1482)

Les représentations figuratives de la constellation d’Orion ont beaucoup changé tout au long de l’histoire de l’Uranométrie (discipline qui traite des cartes du ciel), jusqu’à la disparition des figures mêmes des constellations et l’apparition de la photographie, au XIX^e siècle.

A gauche, représentation médiévale (XIIIe siècle). A droite, Orion dans l’Atlas de Bayer (1602), marquant un renouveau de l’Uranométrie.

Disparition du personnage d’Orion, mais maintien des lignes principales de la constellation (Atlas de Dien, 1851)

À partir des années 1950, les cartes du ciel ont été réalisées photographiquement à l’aide d’instruments à large champ, utilisant des émulsions soigneusement calibrées en fonction des différentes longueurs d’onde. Les atlas de l’ESO (European Southern Observatory), tout comme celui réalisé au mont Palomar (Palomar Sky Survey), existent en version « souple » sous forme de films servant principalement à la préparation des observations, ou en version « dure » sous forme de plaques de verre destinées à des mesures de grande précision.

Deux images photographiques modernes de la constellation d’Orion. A gauche: cliché de S. Kohle, Université de Bonn. A droite, cliché d’Akira Fuji.

A gauche, le Baudrier et l’Epée d’Orion. Le baudrier est formée de trois étoiles quasi parfaitement alignées et équidistantes, et de magnitudes voisines (2e grandeur). Sous cet alignement, un autre alignement Nord-Sud, plus faible, marque l’épée d’Orion, dans laquelle la lunette astronomique ou le petit télescope révèlent la fameuse nébuleuse d’Orion (de fait visible faiblement à l’œil nu dans de très bonnes conditions).
A droite, montage montrant la taille des trois étoiles du Baudrier nommées Alnitam, Alnitak et Mintaka, par rapport à notre Soleil : il s’agit clairement de géantes bleues!

La nébuleuse d’Orion

La première mention de cet objet en tant que nébuleuse est due à Fabbri de Peiresc, en 1611, cf. le billet de blog que je lui ai consacré en 2017. Je rappelle juste ici que dès novembre 1610, l’humaniste provençal commence ses observations à la lunette astronomique depuis la terrasse de son hôtel, et le 26 novembre il découvre ensemble la nébuleuse d’Orion, décrite par ces mots : « In Orione media… Ex duabus stellis composita nubecula quamdam illuminata prima fronte referabat coelo non oio sereno » (« Au centre d’Orion, une nébulosité comprise entre deux étoiles en quelque sorte vue de face et éclairée par devant, le ciel n’étant pas parfaitement clair »).

Continuer la lecture de La constellation d’Orion, ou la Main montée au ciel →

Astronomie, Histoire des sciences, Mes publications

Les Chroniques de l’espace illustrées (13) : Femmes en orbite

novembre 23, 2021 Jean-Pierre LUMINET 12 commentaires

Ceci est la treizième de mes « Chroniques de l’espace illustrées ». Si vous souhaitez acquérir mon livre dans sa version papier non illustrée (édition d’origine 2019 ou en poche 2020), ne vous privez pas !

Femmes en orbite

Pionnière de la conquête spatiale, Valentina Terechkova est non seulement la première femme à être allée dans l’espace, mais elle reste, aujourd’hui encore, la seule femme à avoir effectué un vol solitaire en orbite. Son nom, pourtant, ne s’est pas véritablement inscrit dans l’histoire aux côtés de ceux de Iouri Gagarine ou Neil Armstrong.

Nous sommes le 15 juin 1963. Les Russes ont lancé conjointement les deux vaisseaux spatiaux Vostok 5 et 6 pour un vol jumelé. Dans l’un d’entre eux, la robuste Valentina Terechkova, parachutiste d’essai surnommée « la Mouette », établit la liaison radio avec son homologue masculin. « Nous naviguons à une distance rapprochée. Tous les systèmes de nos vaisseaux fonctionnent normalement. Nous nous portons bien. » Suivent les mots de Nikita Khrouchtchev, premier secrétaire du Parti communiste : « On vous appelle “Mouette”, mais permettez-moi de vous appeler “Valia”. Je suis très fier qu’une fille de chez nous, une jeune fille du pays des soviets, soit la première à voler dans l’espace en possession des moyens techniques les plus perfectionnés. »

Une femme en orbite, c’est un choc pour l’opinion publique mondiale. Les Russes marquent un nouveau point dans la course à l’espace. Il faut néanmoins attendre dix-neuf ans pour qu’une seconde femme aille dans l’espace. Une Russe encore, Svetlana Savitskaya, qui en août 1982 passe une semaine à bord d’un vaisseau Saliout.

L’agence spatiale soviétique a reconnu par la suite qu’une tentative d’accouplement humain avait eu lieu à bord, entre Svetlana et l’un des occupants de la station. Ils étaient quatre, on ne sait pas lequel fut l’élu… ou la victime ! Le test était d’essayer de concevoir le premier enfant de l’espace… De retour sur Terre, Svetlana déclara que pendant ce vol « elle s’était bien amusée ! », sans donner plus de précisions, et elle n’aborda plus le sujet par la suite. Elle était déjà mariée avec un pilote d’essai, avec lequel elle eut deux filles bien après l’expérience. Elle volera à nouveau en 1984, devenant aussi la première femme à effectuer une sortie dans l’espace.

Après sa sortie dans l’espace à bord de Saliout 7, Svetlana Savitskaya a poursuivi une carrière politique : en 1989, elle est devenue députée de l’URSS, ainsi que membre du Soviet suprême de l’URSS.

Les Américains, plus misogynes que les Soviétiques, n’ont envoyé leur première astronaute dans l’espace qu’avec la navette spatiale. Ce fut Sally Ride, astrophysicienne de profession, qui vola à bord de Challenger vingt ans après la Mouette. Continuer la lecture de Les Chroniques de l’espace illustrées (13) : Femmes en orbite →

Astronomie, Histoire des sciences, Littérature, Mes publications, Musique

Franz Liszt dans les étoiles (2): 1811-1836

novembre 8, 2021 Jean-Pierre LUMINET 4 commentaires

Suite du billet “de la rhapsodie à l’astéroïde“

Les grandes manifestations du génie doivent faire l’office du soleil: illuminer et féconder.
Franz Liszt

Depuis sa naissance en 1811, placée sous le signe de la Grande Comète, jusqu’à sa mort en 1886, date de célèbres expériences scientifiques relatives à l’éther, Liszt a été l’exact contemporain de découvertes majeures en astronomie. Et même si le compositeur n’a pas exprimé directement son intérêt pour l’exploration scientifique du cosmos, sa passion pour le ciel spirituel, son rapport à la lumière et à l’éther et un certain nombre de ses compositions comprenant lieder, transcriptions, oratorios et œuvres pianistiques, rendent pertinent d’inscrire une partie de sa trajectoire humaine et artistique dans les étoiles. Et puis n’a-t-il pas été lui-même l’une des plus grandes « stars » de son époque, et n’a-t-il pas fréquenté la plupart des autres stars littéraires et artistiques de son temps ?

Dans se second billet reprenant en partie le dernier chapitre de mon livre “Du piano aux étoiles” en l’agrémentant de son et d’image, aventurons-nous donc en des terres fertiles mêlant musique, science, histoire, et littérature.

Sous le signe de la comète (1811)

Liszt naît le 22 octobre 1811 à Raiding, près de la frontière austro-hongroise (aujourd’hui Doborján, en Autriche). La sage-femme, une bohémienne, lui prédit gloire et prospérité, car une comète passe cette année-là dans le ciel. Elle déclare: « Franzi roulera un jour dans un carrosse d’apparat”.

La Grande Comète de 1811 fut en effet découverte au mois de mars par un astronome amateur vivant en Ardèche. Visible pendant neuf mois à l’œil nu, elle atteint une magnitude voisine de 0, soit celle des plus brillantes étoiles du ciel comme Véga. Ses caractéristiques extrêmement spectaculaires ont profondément marqué les contemporains. Sa conjonction avec une vague de chaleur estivale inédite a suscité des inquiétudes de fin du monde, dont on trouve des échos dans la littérature de l’époque, et même plus tard : dans Guerre et Paix, Léon Tolstoï la décrit comme un présage de mauvais augure. Mais elle est aussi restée associée à une année d’excellents vins, de sorte qu’on la trouve mentionnée dans la Physiologie du goût de Brillat-Savarin, publiée en 1825.

La Grande Comète de 1811, gravures d’époque

L’astronomie à l’aube du XIX^e siècle

En 1781, William Herschel découvre au télescope la première planète invisible à l’œil nu : Uranus. Avant de devenir l’un des plus grands astronomes de son temps, Herschel (1738-1822) avait été compositeur. Durant sa jeunesse passée à Hanovre, il avait reçu une éducation musicale de son père, violoniste et hautboïste. Lui-même devenu hautboïste militaire, il est appelé en Grande-Bretagne en 1756. Libéré de ses obligations militaires, il obtient la direction des concerts d’Édimbourg, puis se retrouve organiste à Bath, dont il va organiser la vie musicale pendant dix ans. Entre 1759 et 1770 il compose 24 symphonies, une douzaine de concertos, des sonates pour clavecin et de la musique religieuse, je dois dire pas toujours très écoutables.

Portrait du jeune William Herschel, et partition de sa symphonie de chambre n°3.

Par bonheur féru d’astronomie, en 1776 il construit un télescope qui grossit 227 fois, le place dans le jardin de sa maison à Bath et, dans la nuit du 13 mars 1781, découvre par hasard la planète Uranus, croyant d’abord avoir affaire à une comète.

William Herschel s’initie à l’astronomie en compagnie de son épouse Caroline. A gauche, polissage du miroir du fameux télescope avec lequel il découvrira la planète Uranus.

Portrait d’Herschel après sa découverte d’Uranus en 1781. Il l’avait d’abord prise pour une comète : à droite, son compte-rendu d’observation que j’ai photographié à la Royal Society of London.

En 1796, le marquis de Laplace publie L’Exposition du système du monde, synthèse de toute la science de son temps qui lui vaudra d’être appelé le « Newton français ». Son ouvrage connaîtra cinq éditions successives jusqu’en 1835. Laplace y lance notamment de nouvelles hypothèses cosmogoniques, dont celle de la « nébuleuse primitive », à l’origine de tous les modèles actuels de formation des systèmes solaires et planétaires. On lui doit aussi la description d’un astre suffisamment massif pour emprisonner la lumière, que l’on appellera un siècle et demi plus tard « trou noir ». J’y reviendrai à la toute fin en évoquant la dernière pièce de Franz Liszt, Unstern, l’étoile du désastre.

On connaît la célèbre réplique que Laplace a adressée à l’empereur Napoléon lorsque ce dernier, après avoir lu son ouvrage, lui ait posé la sempiternelle question : « Et Dieu dans tout ça ? » – « Sire, je n’ai pas eu besoin de cette hypothèse ». Je gage que le très fervent catholique Franz Liszt n’aurait guère apprécié ce point de vue…

Enfin, le premier jour du XIX^e siècle voit la découverte du premier astéroïde par le moine sicilien directeur de l’Observatoire de Palerme, Giuseppe Piazzi. Il sera baptisé (1) Cérès. Comme dit dans le billet précédent, Liszt n’aura « le sien », (3910) Liszt, qu’en 2015.

A gauche : découverte en 1801 par Piazzi du premier astéroïde baptisé Cérès. Au centre, schéma de la ceinture principale d’astéroïdes entre Mars et Jupiter. A droite, le livre que je leur ai consacré.

Naissance d’une étoile (1822-1827)

L’autoritaire père de Franz, Adam Liszt, en digne successeur de Leopold Mozart, enseigne le piano à son fils dès son plus jeune âge, lequel, on s’en doute, révèle très vite d’exceptionnelles capacités à la fois techniques et musicales.

Carl Czerny (1791-1857) et Antonio Salieri (1750-1825), professeurs du jeune Liszt à Vienne

En 1822-1823, Franz travaille à Vienne, auprès de Salieri pour la composition et le chant, et de Czerny pour la technique pianistique. C’est ce dernier qui, le 13 avril 1823, organise une rencontre entre son élève et Beethoven. Le vieux lion étant devenu complètement sourd, on ne sait ce qu’il retint vraiment de l’audition. Mais on sait que pour Liszt cette rencontre, au cours de laquelle il exécuta devant Beethoven une des œuvres du maître, fut inoubliable. Il lui voua toute sa vie un culte, devint l’un de ses plus grands interprètes, et à partir de 1835, organisa de nombreux concerts de ses œuvres dans toute l’Europe.

Liszt joue devant Beethoven, gravure par Rudolf Lupus. Buste de Beethoven moulé par Danhauser (photographie que j’ai prise au Musée Franz Liszt de Budapest).

En 1824, la famille Liszt s’installe à Paris. On connaît l’histoire de la candidature de Franz au Conservatoire, refusée par son directeur italien Luigi Cherubini, qui invoque un article du règlement en vertu duquel les étrangers ne peuvent pas s’inscrire.

Franz reçoit alors des leçons privées de composition d’Anton Reicha et de Ferdinando Paër. En parallèle il mène des tournées européennes d’enfant prodige ; la presse parisienne l’affuble du sobriquet de « petit Litz ».

Anton Reicha (1770-1836) et Ferdinando Paër (1771-1839), professeurs de composition du jeune Liszt à Paris

En 1827, son père meurt à Boulogne-sur-Mer de la fièvre typhoïde, il n’ a que cinquante ans. Franz, qui en a quinze, fait venir sa mère, qui passera le reste de jours en France.

A gauche, portrait de jeunesse d’Adam Liszt, violoncelliste et secrétaire du prince Esterházy. Au centre, Anna Liszt (née Lager), mère de Franz. A droite, mémorial d’Adam Liszt au cimetière de Boulogne-sur-Mer.

Continuer la lecture de Franz Liszt dans les étoiles (2): 1811-1836 →

Histoire des sciences, Mes publications, Sciences

Les Chroniques de l’espace illustrées (12) : Combien ça coûte ?

août 24, 2021 Jean-Pierre LUMINET 4 commentaires

Ceci est la douzième de mes « Chroniques de l’espace illustrées ». Si vous souhaitez acquérir mon livre dans sa version papier non illustrée (édition d’origine 2019 ou en poche 2020), ne vous privez pas !

Combien ça coûte ?

Combien de fois n’entend-on pas dire que l’argent mis en jeu dans l’exploration spatiale serait mieux dépensé sur Terre, à combattre la pauvreté, la faim dans le monde, les maladies, le réchauffement climatique, la pollution et autres fléaux du monde moderne ?

Plusieurs commentateurs de ce blog, au demeurant prolifiques et pleins de sapience, ne se privent pas de me faire régulièrement remarquer la misère de la condition paysanne dans la France d’aujourd’hui.

La question se posait déjà il y a cinquante ans… En 1970, en plein succès du programme Apollo, le directeur scientifique de la Nasa, Ernst Stuhlinger, reçoit une lettre de sœur Mary Jucunda, officiant en Zambie, qui lui reproche de dépenser des milliards de dollars pour la recherche spatiale alors que tant d’enfants meurent de faim. Dans une réponse d’anthologie, Stuhlinger détaille longuement les arguments justifiant les dépenses spatiales.

Il explique, par exemple, comment le satellite terrestre artificiel, en orbite autour du globe à très haute altitude, peut observer de vastes aires de terrain en un temps très court, mesurer une grande variété de facteurs indiquant l’état des cultures, du sol, les sécheresses, les précipitations, la couverture de neige, et communiquer ces informations aux stations au sol afin d’améliorer les programmes de production de nourriture.

Début de la réponse d’Ernst Stuhlinger à sœur Jucunda

Il souligne ensuite que, chaque année, un millier d’innovations techniques générées par le programme spatial sont recyclées dans les technologies terrestres. On lui doit, par exemple, les ordinateurs modernes, l’imagerie médicale, la téléphonie mobile et les chaînes de télévision par satellite, les prévisions météo, le guidage automobile par GPS, les mousses à mémoire de forme, les détecteurs de fumée, les airbags de sécurité dans les voitures, des médicaments mis au point en microgravité, et ainsi de suite. Au final, un programme spatial à quelques milliards de dollars apporte tellement de nouvelles technologies que ses retombées au bénéfice de l’humanité dépassent de loin le coût de sa mise en œuvre. Continuer la lecture de Les Chroniques de l’espace illustrées (12) : Combien ça coûte ? →

Histoire des sciences, Mes publications, Sciences

Les Chroniques de l’espace illustrées (11) : De Mir à la Station spatiale internationale

février 28, 2021 Jean-Pierre LUMINET 19 commentaires

Ceci est la onzième de mes « Chroniques de l’espace illustrées ». Si vous souhaitez acquérir mon livre dans sa version papier non illustrée (édition d’origine 2019 ou en poche 2020), ne vous privez pas !

De Mir à la Station spatiale internationale

À la fin des années 1960, deux objectifs se présentent aux explorateurs de l’espace : d’une part la Lune, qui est facilement accessible depuis la Terre après un voyage de trois jours ; d’autre part, faire vivre des Hommes dans l’espace pour les préparer aux vols de plusieurs mois, voire plusieurs années vers la planète Mars. Les Soviétiques sont convaincus que cette dernière option est la plus importante sur le long terme, d’autant qu’ils doivent bien admettre leur défaite dans la course à la Lune.

C’est ainsi qu’en 1971, en plein déroulement du programme Apollo, la Russie place discrètement en orbite terrestre un nouveau véhicule spatial du nom de Saliout, qui veut dire « salut ». Ce gros satellite de 19 tonnes, offrant un espace habitable de 100 mètres cubes pour trois cosmonautes, est la première station spatiale orbitale.

Timbre soviétique datant de 1972 commémorant la mission Saliout 1. Les choses n’avaient pas été faciles. Lancée le 19 avril 1971 par une fusée Proton depuis le cosmodrome de Baïkonour, Saliout 1 est d’abord placée en orbite sans passagers. Un premier équipage de trois hommes est lancé quatre jours plus tard à bord d’un vaisseau Soyouz; il parvient à réaliser la manœuvre de rendez-vous et à s’amarrer à la station spatiale, mais ne peut y pénétrer à cause d’une écoutille qui reste obstinément fermée. Ils doivent renoncer et revenir sur Terre. Le 6 juin 1971 Soyouz 11 emporte un nouvel équipage de trois cosmonautes qui réussissent cette fois toutes les manœuvres. Ils restent 23 jours à bord, non sans avoir essuyé entre temps un feu dans leur étroit habitacle. Leur retour sur Terre est encore plus catastrophique : ils meurent tous trois, privés d’oxygène à la suite de le dépressurisation de leur module de descente. Ils ont droit à des funérailles nationales et leurs cendres sont scellées dans le mur du Kremlin.

L’équipage de la mission Soyouz 11 composé de Gueorgui Dobrovolski, Viktor Patsaïev et Vladislav Volkov, qui finira tragiquement.

Deux ans plus tard, l’Amérique suit la même voie en plaçant en orbite permanente le troisième étage de sa grande fusée lunaire Saturn 5, rhabillée pour l’occasion en une station orbitale baptisée Skylab.

Dans ces espaces réduits, les astronautes éprouvent le stress du confinement et de la promiscuité, aggravée par les malaises du début du vol en apesanteur et les difficiles conditions hygiéniques, qui rendent invivables les séjours de longue durée.

Ensemble long de 35 mètres et d’une masse de 90 tonnes dont le module principal est réalisé à partir du troisième étage de la fusée lunaire géante Saturn V, Skylab est mise en orbite le 14 mai 1973. Le premier équipage la rejoint quelques jours plus tard. Trois équipages y séjourneront entre 1973 et 1974, dont le dernier, durant près de 84 jours, établira un record provisoire. Les astronautes réalisent à bord de nombreuses observations scientifiques et étudient l’adaptation de l’homme à l’espace. Ici l’astronaute Conrad teste le système de douche.

C’est avec le lancement de la station orbitale Mir, en 1986, que les Soviétiques marquent un pas décisif dans les opérations de survie d’équipages. Avec l’arrimage de cinq modules, la station s’agrandit de façon importante, et une quantité d’améliorations de tous ordres, comme la relève d’équipage et les cargos de ravitaillement, permet d’envisager des vols de plus de six mois.

Superbe photographie de la station russe Mir et ses cinq modules d’habitation, prise depuis la navette spatiale Atlantis en 1997.

La station s’ouvre alors aux vols internationaux, dans lesquels les Américains prennent une part très active. Mir sera une grande réussite. Restée quinze ans en orbite, elle a accueilli 103 passagers appartenant à 13 nations, et a permis de faire 23 000 expériences scientifiques dans l’espace.

Russes et Américains réunis dans la station spatiale Mir en 1995

Mais avec le vieillissement de la station et l’effondrement économique de la Russie, Mir est abandonnée en 2000 et se désintègre lors de son retour sur Terre, l’année d’après. Continuer la lecture de Les Chroniques de l’espace illustrées (11) : De Mir à la Station spatiale internationale →

Actualités, Astronomie, Essai

Oumuamua, vaisseau extraterrestre ou astéroïde extrasolaire?

février 11, 2021 Jean-Pierre LUMINET 9 commentaires

En octobre 2017, un objet en provenance de l’espace interstellaire est repéré par le télescope Pan-STARRS 1 à Hawaï : il traverse notre système solaire, passant relativement près de la Terre (à 30 millions de kilomètres). C’est le premier de ce type à être détecté. Baptisé Oumuamua (« éclaireur » en langue hawaïenne), il suscite aussitôt l’intérêt des astronomes. D’où vient-il, de quoi est-il composé, quelle est son histoire ?

La trajectoire d’Oumuamua, hyperbolique et fortement inclinée par rapport au plan de l’écliptique, indique qu’il s’agit d’un objet interstellaire. Après être passé au plus près du Soleil en septembre 2017, il poursuit son voyage vers la constellation de Pégase.

Des observations ultérieures effectuées en radioastronomie suggèrent qu’Oumuamua est environ dix fois plus long que large, de couleur rouge foncé, dense et riche en métal. Une vue d’artiste le représentant en forme de cigare circule avec succès sur Internet.

Une spectaculaire vue d’artiste attribuant à Oumuamua une forme très allongée, qui a fait la une des médias.

Les spécialistes des “petits corps” estiment qu’il s’agit d’un astéroïde ou d’une comète expulsé de son système planétaire d’origine, peut-être vestige d’une planète déchiquetée. Mais pour Avi Loeb, président du Département d’Astrophysique de Harvard, sa forme est trop étrange pour être naturelle.

Abraham (Avi) Loeb, au Département d’Astronomie de l’Université de Harvard.

Dans un très sérieux article publié fin 2018 avec un de ses étudiants, il lance l’hypothèse qu’Oumuamua est une sonde interstellaire envoyée vers nous par une civilisation extraterrestre avancée afin de nous délivrer un message. Comme la majorité des collègues, j’avais estimé à l’époque l’idée intelligente et audacieuse, mais farfelue. Elle faisait irrésistiblement penser au scénario de Rendez vous avec Rama, un roman de science-fiction publié en 1973 par Arthur C. Clarke que tous les amateurs du genre connaissent bien.

Loeb a cependant développé sa thèse dans un livre qui bénéficie d’une sortie mondiale (heureux auteurs anglo-saxons et formidable machine éditoriale américaine !), dont la version française s’intitule Le premier signe d’une vie intelligente extraterrestre.

A priori c’est le genre de livre à sensation qui m’aurait de prime abord agacé. Cependant, je connais son auteur. Loin d’être un de ces vulgarisateurs fantaisistes qui font de temps en temps la une des médias avec des titres accrocheurs, Loeb est un authentique scientifique qui a publié de très sérieux articles sur un large éventail de sujets, allant de la cosmologie aux trous noirs. Je suis donc bien placé pour apprécier ses contributions. Il m’avait d’ailleurs personnellement reçu en juin 2019 à Harvard, lors du dîner de gala de la conférence organisée pour fêter la première image télescopique d’un trou noir obtenue deux mois plutôt par son équipe, et qui confirmait mes calculs effectués 40 ans auparavant (d’où l’invitation).

Conférence plénière sur l’imagerie des trous noirs que j’ai donnée le 23 mai 2019 à la conférence Black Hole Initiative de l’Université de Harvard, organisée par l’Event Horizon Telescope Consortium. Avi Loeb me tend le micro après son discours de présentation de mes travaux.

Loeb est un esprit particulièrement imaginatif. Avec cet ouvrage grand public il se révèle aussi excellent écrivain, soignant aussi bien le fond scientifique que le style littéraire. On en jugera par cette simple phrase : « une photovoile emportée par la bourrasque d’une supernova me fait penser au pappus duveteux d’une graine de pissenlit, soufflé par le vent vers un sol vierge à féconder ».

Dès l’introduction, il rappelle que l’une des questions fondamentales de l’humanité, sans doute celle qui nous interpelle le plus à travers le prisme de la science, de la philosophie et de la religion, est : sommes-nous seuls dans l’univers ? Et, de façon plus pointue, y a-t-il d’autres civilisations conscientes qui explorent l’espace interstellaire et laissent des témoignages de leurs entreprises ? Continuer la lecture de Oumuamua, vaisseau extraterrestre ou astéroïde extrasolaire? →

Histoire des sciences, Mes publications

Les Chroniques de l’espace illustrées (10) : Piétons du cosmos

janvier 21, 2021 Jean-Pierre LUMINET 4 commentaires

Ceci est la dixième de mes « Chroniques de l’espace illustrées ». Si vous souhaitez acquérir mon livre dans sa version papier non illustrée (édition d’origine 2019 ou en poche 2020), ne vous privez pas !

Piétons du cosmos

Nous sommes le 18 mars 1965. L’URSS lance le vaisseau spatial Voskhod 2 en orbite terrestre avec deux cosmonautes à bord, dont l’ingénieur Alexeï Leonov. Son nom va entrer dans la grande histoire de l’exploration spatiale. Par l’intermédiaire d’un sas ouvert sur le vide, Leonov, équipé d’un scaphandre, effectue la première sortie dans l’espace. Il y passe une vingtaine de minutes, accroché au vaisseau par un simple cordon.

Cliché historique de Leonov effectuant la première sortie dans l’espace.

La télévision soviétique retransmet des images en temps réel de l’exploit. On voit le cosmonaute flotter à côté du sas dans l’espace cosmique. La mission frôle cependant le drame. Une fois dans l’espace, la combinaison de Leonov, trop gonflée par la pression, devient rigide et l’empêche de rentrer par la trappe de sortie. Après dix minutes de lutte fébrile, il réussit à ouvrir une valve pour la dégonfler et peut retourner à bord, pris de vertiges dus à la baisse de pression, mais sain et sauf.

Retour triomphal à Moscou d’Alexei Leonov et son coéquipier Pavel Beliaïev (à sa gauche). De fait la mission a frôlé la catastrophe à plusieurs reprises, et ce sera le dernier vol de la série Voskhod. Outre le problème de la combinaison de Leonov, le système d’orientation automatique du vaisseau permettant sa rentrée atmosphérique s’est révélé déficient. Les deux cosmonautes ont réussi à la faire manuellement, atterrissant cependant à 400 km de la zone prévue dans deux mètres de neige, et passant deux jours dans la nature avant d’être récupérés !

L’événement fait grand bruit. Trois mois plus tard, Edward White fait la première sortie américaine dans l’espace durant seize minutes, s’aidant d’un pistolet à air comprimé pour maîtriser ses mouvements.

Première sortie américaine le 3 juin 1965, avec Edgar White.

Ces deux exploits marquent le début des sorties extravéhiculaires, c’est-à-dire les activités réalisées à l’extérieur d’un véhicule spatial par un astronaute revêtu d’une combinaison. Par la suite et pour des raisons de sécurité, les astronautes effectueront leurs sorties en binôme et resteront attachés au véhicule spatial par un câble, jusqu’à ce qu’en 1984 Bruce McCandless soit le premier à réaliser une sortie autour de la Terre sans être relié au vaisseau, se mouvant dans l’espace au moyen d’un fauteuil équipé de petits propulseurs – auxquels il fallait faire pleinement confiance !

La spectaculaire première sortie extravéhiculaire “libre” (sans cordon ombilical) effectuée par Bruce McCandless lors de la mission STS-41B de la navette spatiale Challenger. Dans une interview donnée en 2015, il a commenté ainsi sa sortie “Ma femme [Bernice] était dans la salle de contrôle de la mission, et il y avait pas mal d’appréhension. Je voulais dire quelque chose ressemblant à ce que Neil [Armstrong] avait déclaré en se posant sur la lune, alors j’ai dit “C’était peut-être un petit pas pour Neil, mais pour moi c’est un sacré grand saut” . Cela a un peu relâché la tension.”

L’Homme n’étant pas du tout fait pour vivre dans le vide hostile de l’espace sans équipements spéciaux, la combinaison est cruciale. L’équipement doit fournir à l’astronaute l’oxygène, évacuer le dioxyde de carbone et la vapeur d’eau expirés, et assurer une protection thermique tout en autorisant une mobilité maximale. S’ajoutent généralement à ces fonctions un système de communications, une protection partielle contre les rayons cosmiques et les micrométéorites, et la possibilité pour son occupant de boire. Le piéton de l’espace dispose alors d’une autonomie de huit heures au maximum pour mener à bien des tâches extravéhiculaires nécessitant un outillage adapté au port de la combinaison.

Le russe Anatoly Solovyev détient le record du temps passé lors de sorties dans l’espace : 82 heures 22 minutes en 16 sorties distinctes, effectuées en 1997 lors de la mission Mir 24. Il est ici accompagné de l’ingénieur Pavel Vinogradov pour réparer le panneau solaire Spektr endommagé de la station spatiale Mir.

Les premières femmes à sortir dans l’espace ont été une Russe et une Américaine, et en 1988 ce fut le tour d’un Français, Jean-Loup Chrétien, sorti six heures lors d’une mission de la station spatiale russe Mir.

A gauche, timbre commémoratif de la russe Svetlana Savitskaya, première femme à sortir dans l’espace le 25 juillet 1984 (mission Soyuz T-12). A droite, Jean-Loup Chrétien a été en 1982 le premier spationaute Européen (mission franco-russe PVH sur Saliout 7), et le 9 décembre 1988, le premier non-russe et non-américain à effectuer une sortie extra-véhiculaire (Mission Aragatz sur la station Mir). Sa sortie a duré 5h57, alors record de durée pour une EVA.

Continuer la lecture de Les Chroniques de l’espace illustrées (10) : Piétons du cosmos →

Histoire des sciences, Mes publications, Sciences

Les Chroniques de l’espace illustrées (9) : Anecdotes spatiales

décembre 31, 2020 Jean-Pierre LUMINET 3 commentaires

Ceci est la neuvième de mes « Chroniques de l’espace illustrées ». Si vous souhaitez acquérir mon livre dans sa version papier non illustrée (édition d’origine 2019 ou en poche 2020), ne vous privez pas !

Anecdotes spatiales

Il y a la grande histoire de l’exploration spatiale, et puis il y a la petite, celle qui se raconte plaisamment, qui met en avant des détails secondaires mais inattendus de l’action principale. En voici quelques anecdotes.

En 1961, la rentrée atmosphérique du vaisseau russe Vostok 2 manque de tourner à la catastrophe. Le module de service ne se détache pas du module de descente et la séparation n’a lieu que tardivement. Guerman Titov réussit de justesse à s’éjecter, mais son parachute manque de débouler sur un train de marchandises en marche. Arrivé enfin au sol sain et sauf, il s’empare d’une grosse canette de bière et, devant un comité d’accueil médusé, il la siffle d’une traite pour se remettre de ses émotions.

Vostok 2 a emmené Guerman Titov en orbite pour un jour 1 heure et 18 minutes afin d’étudier les effets du manque de gravité sur le corps humain. À l’inverse de son prédécesseur Gagarine, Titov a brièvement pris le contrôle manuel de l’appareil. Sur cette galerie de photos on le voit dans sa cabine souffrir du mal de l’espace, puis se ressaisir et utiliser son appareil photo pour prendre des clichés de la Terre. Après son atterrissage mouvementé il se présente en héros aux officiels venus l’accueillir et siffle une canette de bière.

Autre incartade au strict règlement alimentaire due à l’Américain John Young au cours de la mission Gemini 3 : il emporte en cachette dans la poche de sa combinaison un sandwich au corned-beef et commence à le manger sous les yeux effarés de son copilote Gus Grissom. L’affaire fait scandale, John Young est réprimandé, ce qui ne l’empêchera pas quelques années plus tard de commander la mission Apollo 16, au cours de laquelle il restera soixante et onze heures à la surface de la Lune ! Et après moult rapports et commissions d’experts, le corned-beef sera officiellement autorisé dans les navettes spatiales en 1981.

Gus Grissom et John Young font équipe lors de la mission Gemini 3. A un moment Young sort de la poche de sa combinaison spatiale un paquet. Un dialogue s’ensuit (je traduis en français) : “Qu’est-ce que c’est?” demande Grissom. “Un sandwich au corned-beef, ” répond Young. “D’où ça sort?” demande Grissom. Young explique : “Je l’ai apporté avec moi. Voyons quel goût il a. Ça sent bon, n’est-ce pas?” A droite, un sandwich au corned-beef sous cellophane est exposé au Grissom Memorial Museum (Mitchell, Indiana) pour immortaliser la scène.

Autres fantaisies qui ne sont plus d’ordre culinaire : Neil Armstrong, le héros impavide de la mission Apollo 11 et premier homme à marcher sur la Lune, a pour sa part secrètement emporté un ours en peluche. Continuer la lecture de Les Chroniques de l’espace illustrées (9) : Anecdotes spatiales →

Astronomie, Histoire des sciences, Littérature, Mes publications, Poésie

Les Chroniques de l’espace illustrées (8) : Rêves d’univers

décembre 19, 2020 Jean-Pierre LUMINET 6 commentaires

Ceci est la huitième de mes « Chroniques de l’espace illustrées ». Si vous souhaitez acquérir mon livre dans sa version papier non illustrée (édition d’origine 2019 ou en poche 2020), ne vous privez pas !

Rêves d’univers

« Nous rêvons de voyages à travers l’Univers, mais l’Univers n’est-il pas en nous ? » s’interroge en 1793 le poète allemand Novalis. Dans sa Poétique de l’espace de 1957, Gaston Bachelard évoque à son tour le double univers du cosmos et des profondeurs de l’âme humaine. Science et poésie peuvent faire bon ménage, l’astronomie et l’exploration spatiale étant particulièrement propices aux rêveries poétiques.

Je vous propose une brève promenade dans le jardin enchanté de la poésie cosmique avec quatre textes peu connus. Le premier est extrait d’un grand rêve cosmique intitulé La Comète, publié en 1820 par l’Allemand Jean Paul (de son vrai nom Johann Paul Friedrich Richter) :

« Bientôt ne resta plus de notre ciel que le soleil, semblable à une petite étoile, et les flammèches de quelques queues de comètes qui s’en approchaient. Nous passions maintenant entre les soleils d’un vol si rapide qu’à peine ils prenaient un instant à nos yeux la grandeur de lunes, avant de se fondre, derrière nous, en infimes nébuleuses ; et leurs terres, sur notre passage accéléré, ne nous apparaissaient pas. Enfin, le soleil de notre Terre, Sirius, toutes les constellations et la Voie lactée de notre ciel ne furent plus sous nos pieds qu’une claire nébuleuse au milieu de petites nuées plus lointaines. Ainsi traversions-nous les solitudes étoilées ; les cieux, successivement, s’épanouissaient devant nous et se resserraient derrière nous – et des Voies lactées s’accumulaient dans le lointain, comme l’Arc de Triomphe de l’Esprit Infini. »

Un choix des plus belles rêveries cosmiques de Jean Paul a été traduit en français et commenté par Albert Béguin. En particulier, le récit “La Comète” s’inspire du spectaculaire passage de la Grande comète de 1811 (C/1811 F1), qui resta visible pendant 9 mois à l’œil nu et marqua profondément ses contemporains. Sa conjonction avec une importante vague de chaleur a suscité des inquiétudes de fin du monde, dont on trouve l’écho dans la littérature de l’époque. De façon plus positive, elle est associée à une année d’excellents vins en Europe!

Le deuxième texte est dû à la plume féconde de Blaise Cendrars, grand poète et navigateur devant l’Éternel. En 1926, il écrit L’Eubage, voyage intersidéral au cours duquel des marins lèvent l’ancre et se rendent dans les parages du ciel :

« Nous quittâmes la Terre pour entrer dans cet océan de lumière solaire qu’est notre atmosphère respirable. Ayant atteint ses extrêmes limites, nous nous engageâmes résolument dans les rapides de la région de l’ozone. Nous allions si vite que nous ne pouvions estimer la vitesse acquise et qu’il nous semblait rester immobiles. La Terre était invisible dans notre sillage et devant nous, les astres n’existaient plus. Enfin, nous fîmes la grande chute dans le vide, éclaboussés par une écume d’étoiles. »

Pour Blaise Cendrars, l’exploration spatiale est une pure aventure poétique. Durant sa convalescence après ses blessures de guerre, Jacques Doucet – riche couturier ami des arts et des artistes- lui verse une petite rente mensuelle pour écrire les douze chapitres de “l’Eubage, Aux antipodes de l’Unité” (1926). Il s’agit d’un admirable voyage intersidéral dans lequel les marins lèvent l’ancre, quittent la Terre et se rendent dans les parages du ciel.

Dès l’envol du premier cosmonaute russe, en 1961, le poète Charles Dobzynski s’enthousiasme. Dans son Opéra de l’espace, sa description du décollage d’une fusée réconcilie la poésie la plus pure avec la technologie la plus aride – celle des propulseurs :

« Puissance de l’air lourd, musculature du métal dans le faisceau de la fusée attelée à la foudre, ramification d’éclats et d’explosions dans l’épiderme atmosphérique, avez-vous entendu la stridence de l’astronef striant ce que l’on nommait dérisoirement l’éther ? Oisellerie de flammes, l’astronef s’enfonce dans l’infini avec cet abandon tranquille du dormeur ou du noyé. Le vide est chair, et dans ce ventre sans parois l’astronef-graine fonde le futur. »

Continuer la lecture de Les Chroniques de l’espace illustrées (8) : Rêves d’univers →

Histoire des sciences, Mes publications, Sciences

Les Chroniques de l’espace illustrées (7) : Objectif Lune

décembre 7, 2020 Jean-Pierre LUMINET 8 commentaires

Ceci est la septième de mes « Chroniques de l’espace illustrées ». Si vous souhaitez acquérir mon livre dans sa version papier non illustrée (édition d’origine 2019 ou en poche 2020), ne vous privez pas !

Objectif Lune

Bras de fer symbolique entre Nikita Khrouchtchev et John F. Kennedy à propos de l’affaire des missiles de Cuba, qui a mené les deux blocs au bord de la guerre nucléaire.

1962. La guerre froide bat son plein, exacerbée par la crise des missiles de Cuba. Les activités spatiales militaires permettent de développer au pas de charge toute la panoplie des technologies nécessaires pour envoyer un Homme sur la Lune. Côté américain, les programmes Gemini et Apollo se voient attribuer des budgets colossaux. Côté russe, la station orbitale permanente devient l’objectif à long terme, sans toutefois écarter la Lune des projets immédiats.

Une cinquantaine de missions lunaires américaines et soviétiques vont ainsi se dérouler dans les quinze années qui suivent. Certaines placent en orbite lunaire des satellites transmettant des photographies détaillées de la surface, d’autres font atterrir des modules capables d’analyser le sol de notre satellite naturel.

En 1966, Luna 9 réussit la très délicate manœuvre de l’alunissage en douceur. Le premier drapeau à « flotter » sur la Lune est soviétique !

Le 3 Février 1966, la sonde soviétique Luna-9 est le premier vaisseau spatiale à se poser en douceur sur la Lune. Les 4 et 5 février , elle transmet 3 clichés panoramiques pris par une caméra optique mécanique spécialement construite par les ingénieurs russes. Les images sont transmises sous forme de signaux vidéo analogiques à un débit équivalent à 500 pixels/ligne.

Pour ne pas rester en arrière, les Américains réussissent à leur tour l’alunissage avec la sonde Surveyor 1, et à peine un an plus tard Surveyor 6 est le premier module capable de redécoller.

Le programme Surveyor de la NASA a, entre juin 1966 et janvier 1968, expédié sept sondes automatiques sur la Lune pour démontrer la faisabilité d’un alunissage en douceur. .Cinq vaisseaux, dont le premier Surveyor 1, y sont parvenus, mais deux ont échoué : Surveyor 2 s’est écrasé après une correction de trajectoire ratée, and Surveyor 4 a explosé avant d’atteindre le sol. Le 17 novembre 1967, les moteurs de Surveyor 6 sont mis à feu durant 2,5 secondes, ce qui permet à la sonde de décoller du sol lunaire de 3 à 4 mètres et d’atterrir à 2,4 mètres de sa position d’origine. Ce « saut de puce » lunaire a été le premier décollage depuis la surface de notre satellite.

Cinq sondes Lunar Orbiter sont placées en orbite pour cartographier 99 % de la surface lunaire et définir les sites d’atterrissage des missions Apollo.

Cette photographie du cratère Copernicus prise par la sonde Orbiter 2 le 24 Novembre 1966 a suscité un tel enthousiasme qu’elle a été baptisée “Image du siècle”.

Pour des raisons de mécanique céleste, le voyage Terre-Lune aller-retour se présente de façon optimale lors de certaines fenêtres de tir périodiques et prévisibles. Une fenêtre se présente fin décembre 1968. Le premier vol humain en orbite lunaire est réalisé par le vaisseau Apollo 8, dont les trois membres d’équipage passent Noël à 380 000 kilomètres de chez eux. Les missions s’enchaînent avec succès.

Apollo 8 est le premier vaisseau spatial avec équipage à atteindre la Lune, à s’y mettre en orbite sans se poser et à en revenir. Les trois astronautes Frank Borman, James Lovell et William Anders sont les premiers à assister à un lever de Terre depuis son satellite naturel et à le photographier. A gauche, photo de l’équipe en orbite autour de la Lune, Borman au centre. A droite, première image de la Terre entière prise par les humains, probablement photographiée par William Anders. Le Sud est en haut, l’Amérique du Sud est au milieu.

En mai 1969, Apollo 10 se met en orbite lunaire et teste toutes les manœuvres conçues pour l’alunissage.

La Terre, la Lune et l’alunisseur d’Apollo 10 vus de la capsule orbitale en mai 1969. Apollo 10, quatrième mission avec équipage du programme américain, est une répétition générale pour le premier atterrissage lunaire qui aura lieu deux mois plus tard.

Enfin le 21 juillet 1969, Apollo 11 dépose le module Eagle sur la mer de la Tranquillité. Continuer la lecture de Les Chroniques de l’espace illustrées (7) : Objectif Lune →

Histoire des sciences, Mes publications, Sciences

Les Chroniques de l’espace illustrées (6) : Animaux dans l’espace

novembre 21, 2020 Jean-Pierre LUMINET 4 commentaires

Ceci est la sixième de mes « Chroniques de l’espace illustrées ». Si vous souhaitez acquérir mon livre dans sa version papier non illustrée (édition d’origine 2019 ou en poche 2020), ne vous privez pas !

Animaux dans l’espace

Avant que des êtres humains soient embarqués dans l’espace, ce sont nos amis les animaux qui ont servi de cobayes. Le 19 septembre 1783 déjà, un coq, un mouton et un canard font l’expérience du premier vol habité en montgolfière. Cela se passe devant le château de Versailles, en présence du roi Louis XVI. Leur nacelle s’élève jusqu’à 480 mètres de hauteur avant de redescendre, ils sont recueillis bien vivants.

Deux gravures d’époque illustrant le vol en montgolfière du 19 septembre 1783 avec des animaux. Contrairement à ce suggère l’illustration de droite, l’expérience s’est effectuée en grande pompe au Château de Versailles, devant le Roi. Un mouton, un coq et un canard (enfermés dans un panier d’osier et non pas à l’air libre!) furent ainsi les premières créatures vivantes à voler dans une machine fabriquée de main d’homme.
On alluma d’abord un feu, alimenté par de vieilles chaussures, de la viande en décomposition et de la paille humide afin de faire beaucoup de fumée – on croyait alors que c’était la fumée qui ferait élever l’engin, et non pas l’air chaud. Quand tout le monde lâcha en même temps les cordes qui retenaient le ballon au sol, ce dernier s’éleva majestueusement mais une rafale la renversa sur le côté. Heureusement l’aérostat se redressa, s’éleva à près de 500 mètres et atterrit trois kilomètres plus loin. À part une dispute entre le coq et le chien, tout s’était bien déroulé….

L’aventure spatiale du XX^esiècle offre un scénario identique, à ceci près qu’un vol à bord d’une fusée ou d’un satellite artificiel est autrement périlleux qu’une simple ascension en ballon dans la basse atmosphère. Au départ, les scientifiques ne savent pas si l’être humain peut survivre aux fortes accélérations de départ et aux longs séjours en apesanteur. Dès 1948, Américains et Soviétiques commencent donc à expérimenter avec des animaux. Les Russes utilisent d’abord des lapins, des rats et des souris pour des vols sans retour, puis des chiennes, qu’ils tentent de ramener vivantes sur Terre. Les Américains préfèrent les singes, dont la physiologie est plus proche de celle de l’Homme. Nombre d’entre eux sont sacrifiés au nom de la science, lors des phases de décollage, de retour au sol des fusées, ou dans les vols orbitaux.

Les premières créatures vivantes envoyées dans l’espace ont été des mouches à fruits, à bord d’une fusée V2. Lors du vol du 20 février 1947 elles ont atteint une altitude de 108 km, puis ont été récupérées vivantes dans une petite capsule parachutée. Trois quarts de siècle plus tard on continue à étudier leur comportement dans l’espace à bord de la Station Spatiale Internationale. En 1953 l’US Air Force a fait un film sur le comportement de souris dans l’espace. A droite, le premier singe dans l’espace, Albert II, a atteint le 4 juin 1949 une altitude de 134 km mais a péri à la descente à cause d’un problème de parachute. Ses congénères Albert I, II et IV ont également péri dans l’explosion de leurs fusées.

C’est ainsi que le 3 novembre 1957, une chienne noir et blanc nommée Laïka embarque à bord de Spoutnik 2. Le lancement est effectué sans tests préliminaires et dans la précipitation, s’agissant de damer le pion aux Américains. Le satellite atteint effectivement son orbite, Laïka est le premier être vivant à voyager dans l’espace interplanétaire. Las, il n’a jamais été prévu que Spoutnik 2 revienne. Équipée d’une combinaison de cosmonaute et enfermée dans un petit habitacle, Laïka s’affole au décollage, son cœur bat la chamade. Après la mise sur orbite, la température de la capsule monte à 41 degrés. Laïka met cinq heures à mourir de déshydratation, de chaleur et de convulsions. Spoutnik 2 se consumera dans l’atmosphère quelques mois plus tard. Quarante ans après, une statue a été érigée à Moscou en l’honneur de Laïka. On lui devait bien cela.

Commémoration du vol de Laïka à bord de Spoutnik 2 le 3 novembre 1957

Heureusement, beaucoup d’animaux ont survécu. C’est notamment le cas avec la mission Spoutnik 5, en 1960, qui embarque 2 chiennes nommées Belka et Strelka, 40 souris, 2 rats, des centaines d’insectes, des végétaux tels que maïs, blé, oignons et champignons, des bactéries et des préparations de peau humaine. Tous sont récupérés sur Terre en parfait état. Strelka a plus tard donné naissance à 6 chiots, dont l’un a été offert à John Kennedy pour son fils ! Continuer la lecture de Les Chroniques de l’espace illustrées (6) : Animaux dans l’espace →

J’eus le vertige et je pleurai car mes yeux avaient vu cet objet secret et conjectural dont les hommes usurpent le nom, mais qu’aucun homme n’a regardé : l’inconcevable univers. Jorge Luis Borges, L’Aleph (1949)

La Lune

Le mal de l’espace

Une recomposition complexe

Disque d’accrétion ou anneau de photons?

La navette spatiale

La nébuleuse d’Orion

Femmes en orbite

Sous le signe de la comète (1811)

L’astronomie à l’aube du XIXe siècle

Naissance d’une étoile (1822-1827)

Combien ça coûte ?

De Mir à la Station spatiale internationale

Piétons du cosmos

Anecdotes spatiales

Rêves d’univers

Objectif Lune

Animaux dans l’espace

J’eus le vertige et je pleurai car mes yeux avaient vu cet objet secret et conjectural dont les hommes usurpent le nom, mais qu’aucun homme n’a regardé : l’inconcevable univers. Jorge Luis Borges, L’Aleph (1949)

L’astronomie à l’aube du XIX^e siècle