Archives pour la catégorie Actualités

Actualités, Astronomie

Première image du trou noir galactique Sagittarius A*: un décryptage inédit

12 commentaires

Après cinq années de calculs et d’analyses, la collaboration internationale du télescope Event Horizon (EHT) a livré le 12 Mai 2022 l’image de Sagittarius A* (Sgr A*), le trou noir géant tapi au centre de notre galaxie (la Voie lactée), à 27 000 années-lumière de la Terre. Jusqu’à présent, on ne percevait qu’indirectement sa présence, à partir de quelques émissions dans le domaine radio et l’observation des trajectoires des étoiles orbitant à grande vitesse autour d’une masse gigantesque mais invisible. Après celle obtenue par l’EHT en 2019 du trou noir central de la lointaine galaxie M87, c’est donc la seconde image directe de ce type d’astre dont on dispose à ce jour.

Figure 1. Première image du trou noir géant Sagittarius A* situé au centre de la Voie lactée, dévoilée par les équipes du programme international de radioastronomie Event Horizon Telescope. © EHT Collaboration/ESO
Une recomposition complexe

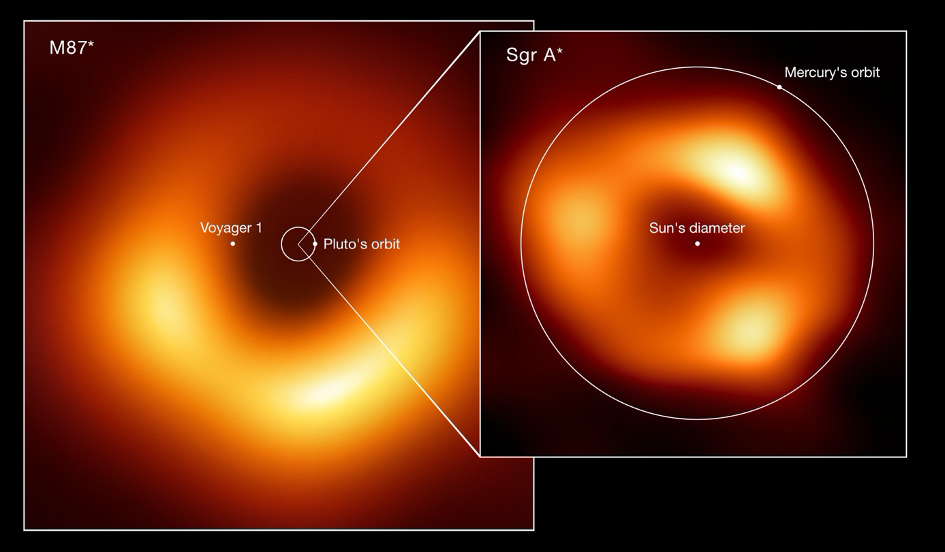
Souvenez-vous. La toute première image télescopique d’un trou noir entouré d’un disque de gaz chaud avait été dévoilée en avril 2019 par les mêmes équipes de l’EHT : il s’agissait du trou noir M87* situé au centre de la galaxie elliptique géante M87, distante de 56 millions d’années-lumière. Les observations de Sgr A* avaient été effectuées en avril 2017, lors de la même campagne que celles de de M87*. S’il a fallu cinq années d’analyse pour Sgr A* contre deux pour M87*, c’est parce que durant le temps de pose des observations – de l’ordre de l’heure – , l’émission lumineuse du disque de gaz autour de Sgr A* est très variable, alors que celle autour de M87* est figée. La raison tient à ce que Sgr A* a une masse 1500 fois plus faible que M87* (4 millions de masses solaires pour SgrA* contre 6 milliards pour M87*), de sorte que l’échelle de temps caractéristique de la variabilité lumineuse, donnée par la simple formule  GM/c3, est beaucoup plus rapide : 20 secondes, contre plusieurs heures pour M87*.

Figures 2a-b. En haut, le montage illustre l’énorme différence de tailles entre M87* et SgrA*, rapportées à la taille de notre système solaire. En bas :en raison de sa taille géante, la structure lumineuse autour de M87* a très peu varié au cours des 4 jours d’observations effectuées en avril 2017.

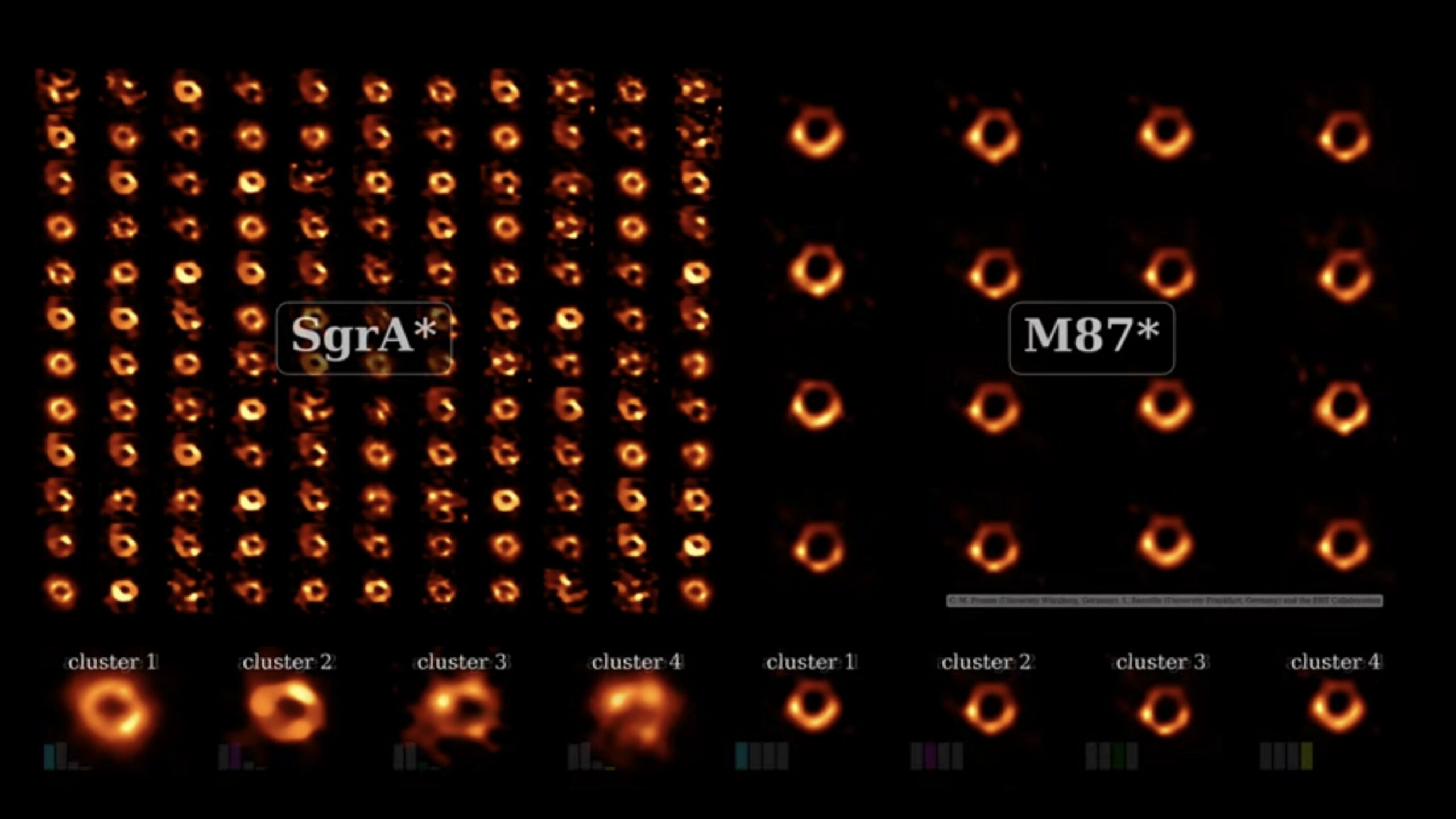
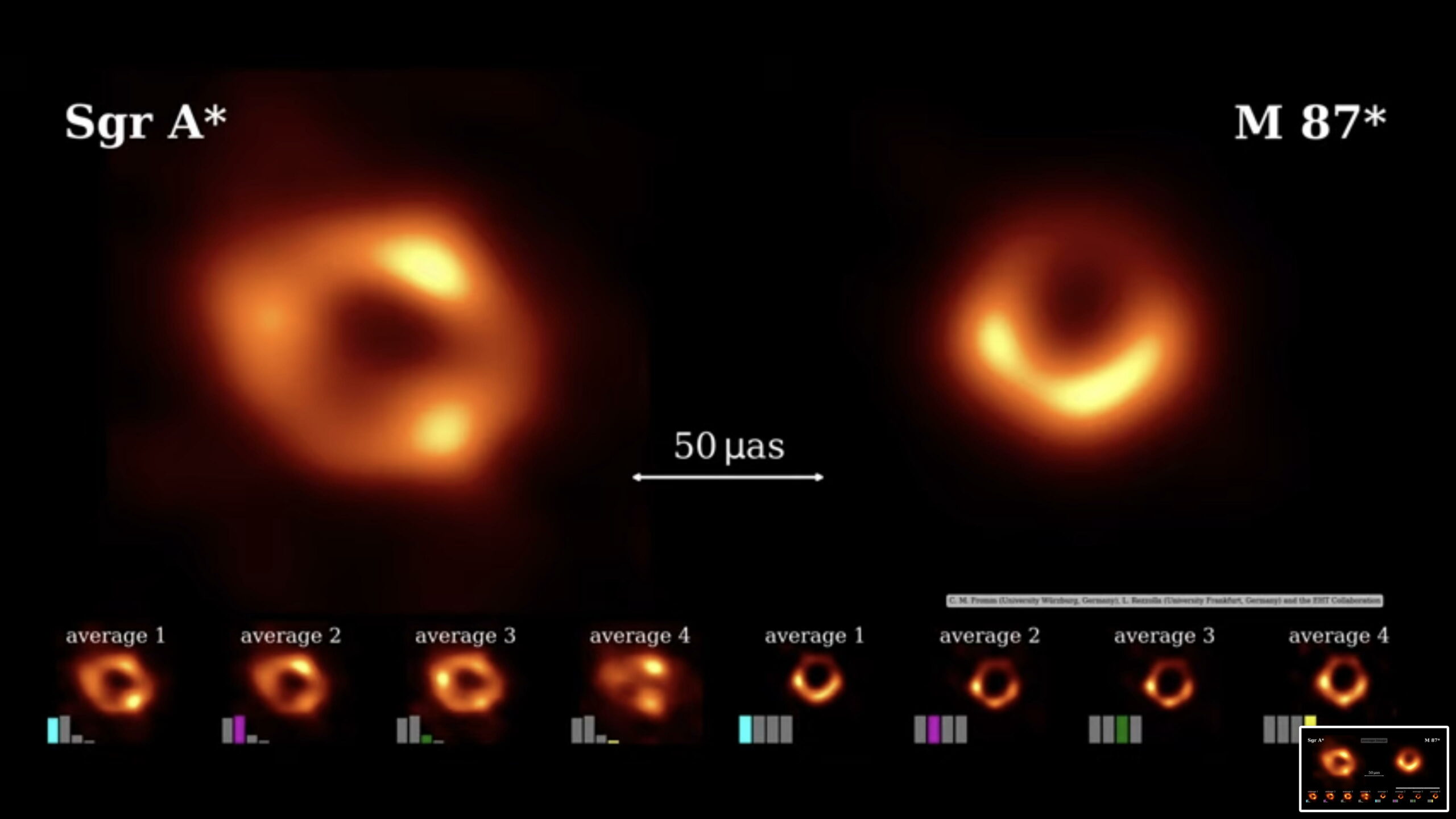
Tenter de capturer une image nette de SgrA* dans un temps de pose d’une heure revenait donc à prendre la photo d’un chien courant après sa queue. Il a fallu un travail d’intégration  considérable pour reconstruire une image “moyenne” de SgrA* suffisamment nette, comme le montre clairement la figure 3.

Figures 3a-b. A gauche, plusieurs dizaines de clichés de SgrA* montrent sa grande variabilité temporelle, au point que la reconstruction d’une image moyennée ne peut reproduire précisément l’état du flot d’accrétion (position incertaine des surbrillances). A droite en revanche, pour M87*, en raison de sa taille géante, la structure lumineuse qui l’entoure a très peu varié au cours des 4 jours d’observations effectuées en avril 2017, de sorte que l’image moyenne reflète assez fidèlement l’état réel du flot d’accrétion.

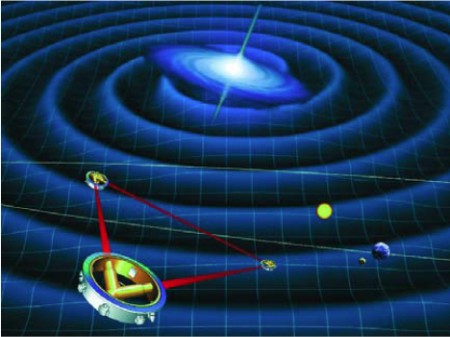
Pour atteindre la résolution angulaire nécessaire pour imager SgrA* et M87*, équivalente à l’angle minuscule sous lequel nous verrions depuis la Terre une pomme sur la Lune, l’EHT a utilisé un réseau de radiotélescopes s’étendant de l’Antarctique à l’Amérique du Nord en passant par le Chili, les îles Hawaï et l’Europe de façon à avoir l’équivalent d’un instrument unique de taille planétaire, fonctionnant en mode interférométrique.    

Figure 4. Les huit radiotélescopes du réseau EHT utilisés en avril 2017

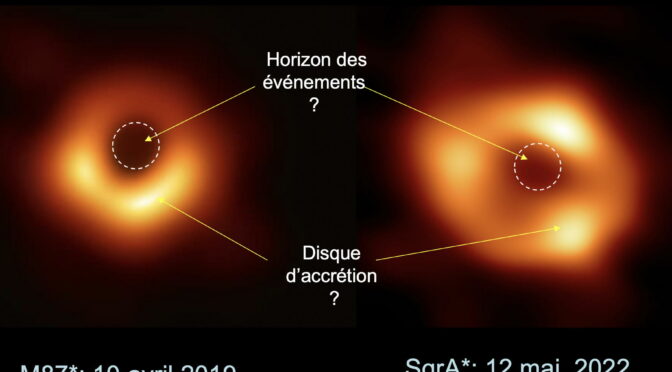
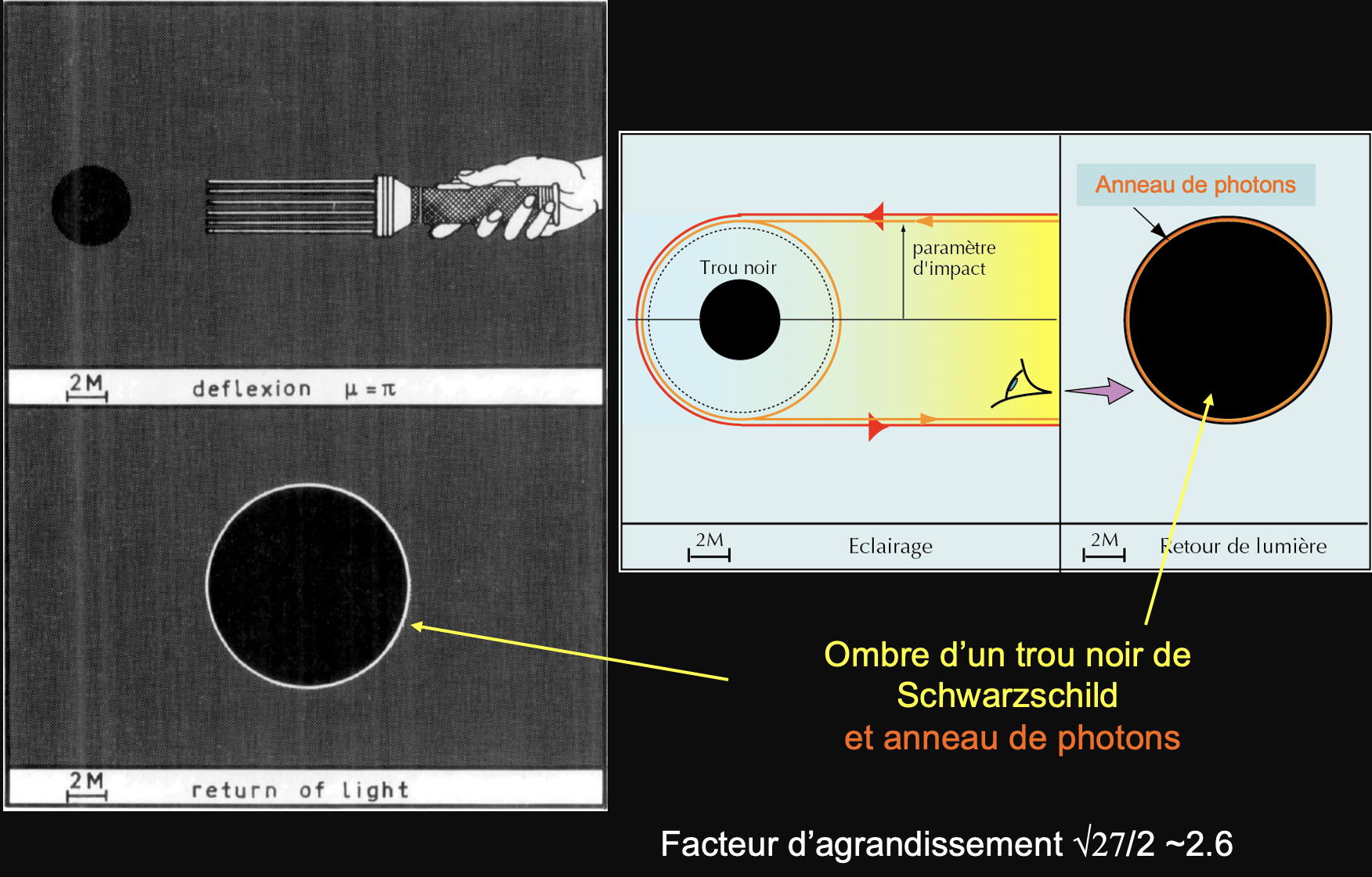
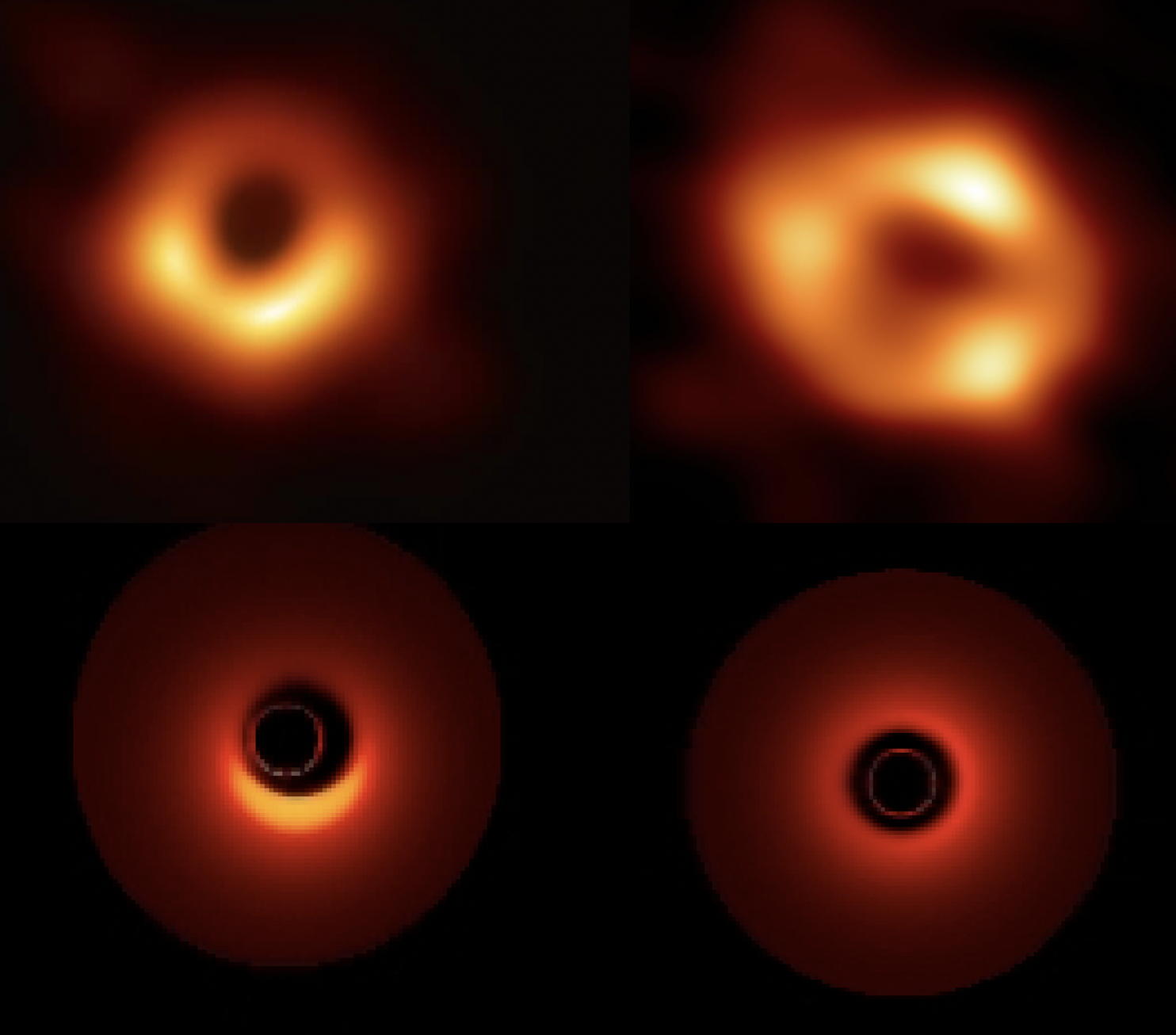
Ce qui frappe de prime abord, c’est que les deux photographies de M87* et de SgrA* se ressemblent beaucoup : au centre, une ombre noire, image de l’horizon des événements (nom donné, je le rappelle, à la surface intangible d’un trou noir) agrandie d’un facteur 2,6 – (comme je l’avais montré dans mon article de 1979, cf. fig. 5), entourée d’une couronne lumineuse jaune-orangée, floue et présentant des taches de surbrillance.

Figure 5. Schémas extraits de mon article de 1979 et de mon ouvrage de vulgarisation “Le destin de l’univers” (2006), illustrant comment “l’ombre” d’un trou noir est l’image agrandie de son horizon des événements d’un facteur 2,6, en raison d’un effet de lentille gravitationnelle. Un anneau de lumière très fin, appelé anneau de photons, l’encercle.
Figure 6. Les deux images télescopiques ressemblantes de M87* et SgrA*

La différence la plus importante est l’apparence de trois taches surbrillantes bien distinctes dans l’anneau lumineux de SgrA*, alors que l’anneau de M87 est continu avec deux zones de surbrillance contigues. De même, l’ombre centrale paraît moins ronde pour SgrA*, sans doute en raison du grand nombre d’images qu’il a fallu intégrer pendant les heures d’observations.

Un catalogue de plusieurs milliers de simulations numériques a été établi aux fins de comparaison avec les clichés de l’EHT et de fixer des plages de valeurs probables pour les caractéristiques physiques (angle de vue, spin, etc)  de SgrA*. Du gaz chaud ionisé tourne rapidement autour du trou noir, formant comme des bras spiraux qui deviennent plus brillants à leur tangence avec l’anneau de photons, où la lumière est amplifiée par lentille gravitationnelle forte. Ce sont ces points brillants qui sont intégrés au cours du temps, et qui donnent la structure générale des couronnes lumineuses.

Figure 7. Il a fallu effectuer des milliers de simulations numériques pour reconstruire une image nette de SgrA*
Disque d’accrétion ou anneau de photons?

Que révèlent au juste ces deux clichés historiques ? A première vue (vue réservée cependant à quelques connaisseurs) on est tenté de les comparer avec les simulations numériques effectuées en 1979 par moi-même et en 1989 avec mon collaborateur Jean-Alain Marck:

Figure 8. Première simulation numérique d’un trou trou noir entouré d’un disque d’accrétion, parue en janvier 1979, avec légendes ajoutées. L’ombre du trou noir est au centre. “L’image du dessus” est l’image directe (dite) primaire du disque d’accrétion, déformée cependant par le champ de gravité. L’ISCO (Inner Stable Circular Orbit) est la dernière orbite stable marquant le bord interne du disque d’accrétion. L’anneau lumineux qui entoure l’ombre  est la superposition de l’anneau de photons et des images secondaire, tertiaire, etc. du disque d’accrétion. L’effet Doppler dû au mouvement du gaz à vitesse relativiste explique la forte asymétrie du flux lumineux apparent vu à grande distance. Le flux lumineux calculé est  cependant “bolométrique”, c’est-à-dire intégré sur toutes les longueurs d’onde du rayonnement électromagnétique.
Figure 9. Simulations numériques effectuées avec Jean-Alain Marck en 1989, reprenant mes calculs de 1979 mais y ajoutant de fausses couleurs et des angles de vue variables, grâce aux progrès des ordinateurs de l’époque.

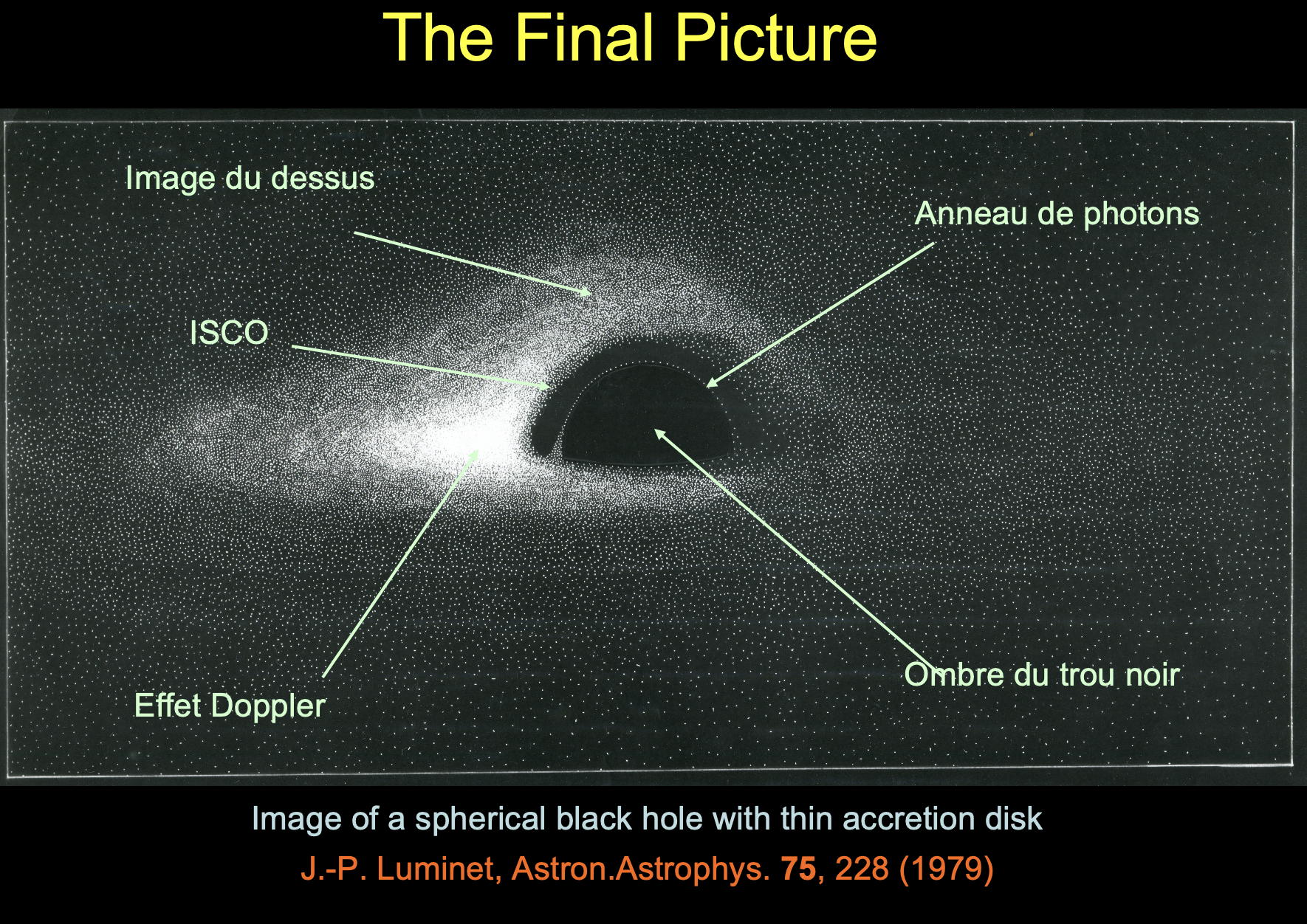
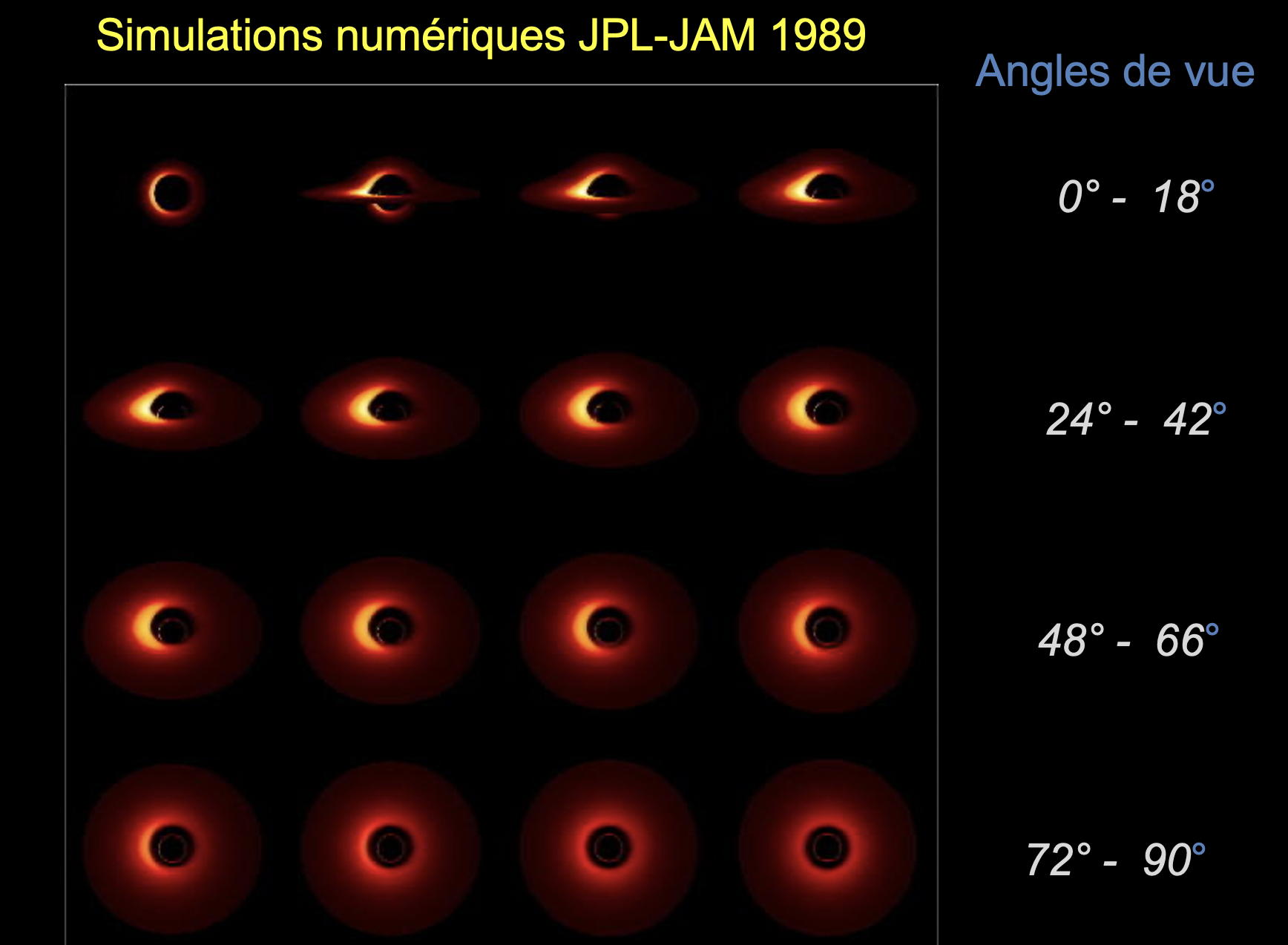
d’en relever les frappantes similitudes :

Figure 10. Ressemblances à première vue frappantes entre les images télescopiques (en haut) et les simulations numériques (en bas)

et d’en tirer des conclusions rapides concernant la structure du disque d’accrétion et l’angle sous lequel il est vu depuis la Terre:

Figure 11. Une interprétation à première vue tentante…

J’avoue m’être moi-même laissé entraîner par cette interprétation, qui d’une part flattait mes calculs pionniers, d’autre part n’était aucunement démentie par les chercheurs de l’EHT, qui m’ont au contraire déroulé un tapis rouge lors de la première conférence tenue sur le sujet à l’Université de Harvard en juin 2019.

Figure 12. Ma conférence de clôture de la Black Hole Initiative Conference tenue à l’Université de Harvard les 20-22 mai 2019 après la publication de la première image télescopique de M87*.

Au point que, tant pour l’image de M87* que pour celle plus récente de SgrA*, cette interprétation a été reprise dans la plupart des médias de vulgarisation scientifique. D’autant que les articles spécialisés  publiés par les chercheurs de l’EHT, bourrés de détails techniques, restent étrangement vagues sur la question…

Or, la réalité physique est toujours plus complexe que nos premières grilles de lecture. Une analyse plus fine, faite depuis 2019 sur M87* et renforcée en 2022 par celle de SgrA*,  suggère que  la couronne lumineuse en forme de « donut » n’est pas l’image directe des disques d’accrétion gazeux orbitant autour de leurs trous noirs respectifs, et que les surbrillances ne reflètent pas complètement l’état réel du gaz autour du trou noir, ni ne traduisent  l’effet Doppler dû à la rotation relativiste du gaz  ! Continuer la lecture →

Actualités, Astronomie, Essai

Oumuamua, vaisseau extraterrestre ou astéroïde extrasolaire?

9 commentaires

En octobre 2017, un objet en provenance de l’espace interstellaire est repéré par le télescope Pan-STARRS 1 à Hawaï : il traverse notre système solaire, passant relativement près de la Terre (à 30 millions de kilomètres). C’est le premier de ce type à être détecté. Baptisé Oumuamua (« éclaireur » en langue hawaïenne), il suscite aussitôt l’intérêt des astronomes. D’où vient-il, de quoi est-il composé, quelle est son histoire ?

La trajectoire d’Oumuamua, hyperbolique et fortement inclinée par rapport au plan de l’écliptique, indique qu’il s’agit d’un objet interstellaire. Après être passé au plus près du Soleil en septembre 2017, il poursuit son voyage vers la constellation de Pégase.

Des observations ultérieures effectuées en radioastronomie suggèrent qu’Oumuamua est environ dix fois plus long que large, de couleur rouge foncé, dense et riche en métal. Une vue d’artiste le représentant en forme de cigare circule avec succès sur Internet.

Une spectaculaire vue d’artiste attribuant à Oumuamua une forme très allongée, qui a fait la une des médias.

Les spécialistes des “petits corps” estiment qu’il s’agit d’un astéroïde ou d’une comète expulsé de son système planétaire d’origine, peut-être vestige d’une planète déchiquetée. Mais pour Avi Loeb, président du Département d’Astrophysique de Harvard, sa forme est trop étrange pour être naturelle.

Abraham (Avi) Loeb, au Département d’Astronomie de l’Université de Harvard.

Dans un très sérieux article publié fin 2018 avec un de ses étudiants, il lance l’hypothèse qu’Oumuamua est une sonde interstellaire envoyée vers nous par une civilisation extraterrestre avancée afin de nous délivrer un message. Comme la majorité des collègues, j’avais estimé à l’époque l’idée intelligente et audacieuse, mais farfelue. Elle faisait irrésistiblement penser au scénario de Rendez vous avec Rama, un roman de science-fiction publié en 1973 par Arthur C. Clarke que tous les amateurs du genre connaissent bien.

Loeb a cependant développé sa thèse dans un livre qui bénéficie d’une sortie mondiale (heureux auteurs anglo-saxons et formidable machine éditoriale américaine !), dont la version française s’intitule Le premier signe d’une vie intelligente extraterrestre.

A priori c’est le genre de livre à sensation qui m’aurait de prime abord agacé. Cependant, je connais son auteur. Loin d’être un de ces vulgarisateurs fantaisistes qui font de temps en temps la une des médias avec des titres accrocheurs, Loeb est un authentique scientifique qui a publié de très sérieux articles sur un large éventail de sujets, allant de la cosmologie aux trous noirs. Je suis donc bien placé pour apprécier ses contributions. Il m’avait d’ailleurs personnellement reçu en juin 2019 à Harvard, lors du dîner de gala de la conférence organisée pour fêter la première image télescopique d’un trou noir obtenue deux mois plutôt par son équipe, et qui confirmait mes calculs effectués 40 ans auparavant (d’où l’invitation).

Conférence plénière sur l’imagerie des trous noirs que j’ai donnée le 23 mai 2019 à la conférence Black Hole Initiative de l’Université de Harvard, organisée par l’Event Horizon Telescope Consortium. Avi Loeb me tend le micro après son discours de présentation de mes travaux.

Loeb est un esprit particulièrement imaginatif. Avec cet ouvrage grand public il se révèle aussi excellent écrivain, soignant aussi bien le fond scientifique que le style littéraire. On en jugera par cette simple phrase : « une photovoile emportée par la bourrasque d’une supernova me fait penser au pappus duveteux d’une graine de pissenlit, soufflé par le vent vers un sol vierge à féconder ».

Dès l’introduction, il rappelle que l’une des questions fondamentales de l’humanité, sans doute celle qui nous interpelle le plus à travers le prisme de la science, de la philosophie et de la religion, est : sommes-nous seuls dans l’univers ? Et, de façon plus pointue, y a-t-il d’autres civilisations conscientes qui explorent l’espace interstellaire et laissent des témoignages de leurs entreprises ? Continuer la lecture →

Actualités, Astronomie, Sciences

Le prix Nobel de physique 2020 pour les trous noirs (2/2) : Genzel et Ghez

8 commentaires

Comme annoncé dans le billet précédent consacré à Roger Penrose, ce second billet « Nobel de physique 2020 » s’attache aux travaux de Genzel, Ghez et consorts sur le Centre Galactique et son putatif trou noir. Putatif, car rien ne prouve encore de façon irréfutable que l’objet compact et massif qui se tient au centre de notre galaxie, Sagittarius A*, est bel et bien un trou noir délimité par son horizon des événements, tel qu’il est décrit par la relativité générale, ou bien un objet exotique aux propriétés similaires, dont l’existence, bien qu’improbable, n’est pas interdite dans certaines théories alternatives de la gravité.

A cet égard il est intéressant de noter que le communiqué de l’Académie des sciences de Suède mentionne que Reinhard Genzel et Andrea Ghez sont récompensés pour « la découverte d’un objet compact supermassif dans le centre de notre galaxie », sans mentionner le terme de trou noir.

Et de fait, les remarquables travaux effectués depuis trente ans par les équipes de Genzel à l’Observatoire Européen Austral du Chili, puis de Ghez au télescope Keck de Hawai, ne démontrent aucunement l’existence d’un trou noir, même si en l’état actuel de nos connaissances cela reste l’hypothèse de loin la plus plausible. Si les observations télescopiques de l’ombre d’un trou noir, effectuées par l’Event Horizon Telescope (EHT) en avril 2017 et publiées en 2019 (dont on aurait pu croire qu’elle leur aurait valu rapidement le Nobel) avait pu fournir l’image de Sagittarius A* plutôt que celle de la plus lointaine source M87*, nul doute que le communiqué aurait été formulé différemment. Mais voilà, à cause de la trop grande variabilité temporelle de la luminosité du disque d’accrétion autour de Sagittarius A*, le complexe programme de reconstitution d’images de l’EHT a pour l’heure pu fournir une indication convaincante de l’existence d’un trou noir dans M87*, mais pas dans Sagittarius A*.

Comme je l’explique plus longuement ci-dessous, les travaux des lauréats Genzel et Ghez ont été consacrés à l’étude de la dynamique orbitale d’étoiles gravitant autour et très près du Centre Galactique, et à en déduire la valeur de la masse de l’objet compact responsable de leurs vitesses « anormalement » élevées.

Je reprends maintenant quelques éléments déjà publiés dans mon ouvrage de 2006 « Le destin de l’univers, trous noirs et énergie sombre » et réactualisés à travers diverses conférences sur le sujet que j’ai récemment données.

Le centre dynamique de la Galaxie, dans la direction de la constellation du Sagittaire, se dissimule à la vue des astronomes par de gigantesques bancs de gaz et de poussières cosmiques. Sur 1 000 milliards de photons émis dans le domaine visible, un seul survit au voyage de 25 000 années-lumière qui le sépare de la Terre. Dans ces conditions, l’observation du centre galactique au moyen des télescopes traditionnels est sans espoir. Par bonheur pour les astronomes, la radiation électromagnétique a un large spectre s’étendant des ondes radio aux rayons gamma, et certaines longueurs d’onde peuvent franchir l’obstacle des poussières. C’est le cas des rayonnements radio, infrarouge, X durs et gamma.

Tout se passe dans une région de 30 années-lumière. La luminosité « bolométrique » – somme de toutes les contributions radio, infrarouge, X, etc. – atteint 10 millions de fois la luminosité solaire. On y trouve deux sources radio : Sagittarius A Est, qui a toutes les caractéristiques d’un reste de supernova, et Sagittarius A Ouest, qui présente une superposition de deux types d’émission radio ; l’une est « thermique », c’est-à-dire qu’elle provient du rayonnement naturel d’un nuage d’hydrogène moléculaire en forme de mini-spirale ; l’autre, au cœur même de Sagittarius A Ouest, est produite par des électrons animés de vitesses proches de celle de la lumière – il s’agit du rayonnement synchrotron.

En haut à gauche: Image radio de Sagittarius A prise au VLA (en fausses couleurs). La région brillante est la source compacte Sagittarius A*, censée abriter un trou noir supermassif.
En bas à gauche:  Zoom sur Sagittarius A Ouest, montrant la structure spirale du nuage d’hydrogène moléculaire.
A droite :  Zoom sur le centre galactique dans le proche infrarouge obtenu en 2002 au VLT. La position de Sagittarius A* est indiquée par les flèches jaunes. Le champ embrasse un peu plus d’une année-lumière.

Cette source non thermique, baptisée Sagittarius A* (l’astérisque évoque son apparence ponctuelle et met en relief l’unicité de cette radiosource au sein du complexe plus large de Sagittarius A), est la plus puissante de toutes les radiosources de la Galaxie. Sa luminosité est 10 fois supérieure à la luminosité optique du Soleil. Mais le plus remarquable est sa compacité : l’émission provient d’une région plus petite que 3 milliards de kilomètres, c’est-à-dire de la taille de l’orbite de Saturne ou celle d’une géante rouge. Il est impossible de « caser » un amas d’étoiles dans un volume aussi faible. L’émission radio est donc due à un astre unique. Quels sont les types d’astres capables d’émettre du rayonnement radio synchrotron ? Pour diverses raisons, les hyopthèses d’un pulsar, d’une source X binaire ou d’un reste de supernova sont exclues. De toute façon, l’astre responsable de l’émission radio ne peut avoir une masse d’ordre stellaire. Si c’était le cas, il serait animé d’une vitesse propre typique de celle des étoiles dans le centre de la Galaxie, qui est de 150 km/s. Cette vitesse se traduirait par un lent déplacement de la source radio sur la sphère céleste. Un tel mouvement n’est pas observé. Les mesures confirment que l’astre doit rester au repos au centre de la Galaxie ; sa masse doit donc excéder largement celle d’une étoile. Reste l’hypothèse d’un trou noir de quelques millions de masses solaires, compatible avec les observations radioastronomiques. Continuer la lecture →

Actualités, Astronomie, Sciences

Le prix Nobel de physique 2020 pour les trous noirs (1/2) : Roger Penrose

12 commentaires

Le prix Nobel de physique 2020 a été annoncé mardi 6 octobre en fin de matinée. L’Académie des sciences de Suède a récompensé trois pionniers de la recherche sur les trous noirs en la personne du théoricien britannique Roger Penrose (à qui va la moitié du prix) pour avoir découvert « que la formation d’un trou noir est une prédiction solide de la théorie de la relativité générale », des astronomes allemand Reinhard Genzel et américaine Andrea Ghez (qui se partagent l’autre moitié) pour « la découverte d’un objet compact supermassif dans le centre de notre galaxie ».

Les trois lauréats 2020 (un peu plus jeunes qu’actuellement !)

Autant dire que j’ai été extrêmement surpris par cette annonce, et ce pour deux raisons. La première est que je ne pensais pas que le prix Nobel serait attribué deux années de suite à l’astrophysique. Souvenons-nous en effet que le prix 2019 était allé à un trio comprenant déjà un théoricien de l’astrophysique, Jim Peebles, pour ses travaux en cosmologie, et aux deux astronomes Michel Mayor et Didier Queloz pour leur découverte observationnelle de la première planète extrasolaire. Cette année la communauté des physiciens s’attendait donc plutôt à un prix récompensant les domaines de la théorie quantique et/ou de la physique des particules ainsi qu’aux innombrables expériences de laboratoire qui s’y rapportent. Il n’en a rien été, et c’est très bon signe pour les sciences de l’univers, qui semblent avoir le « vent en poupe » auprès de l’Académie suédoise !

Ma seconde surprise, bien plus grande encore, est que le prix récompense des travaux sur les trous noirs, ces énigmatiques puits de l’espace-temps dont ni matière ni lumière ne peuvent s’échapper. Non pas que le sujet ne le mérite pas, bien au contraire – je n’ai pas passé pour rien quarante années de passionnantes recherches sur ces objets exotiques ! –, mais c’est le choix des lauréats qui a de quoi surprendre. On m’aurait dit à l’avance : le prix Nobel va récompenser trois chercheurs pour leurs travaux sur les trous noirs, j’aurais immédiatement pensé, pour la partie observationnelle, aux deux directeurs, l’un américain, l’autre européen, de l’Event Horizon Telescope – qui, je le rappelle, à l’issue d’une quête de près de 20 ans, a délivré en avril 2019 la première image télescopique du trou noir géant situé au centre de la galaxie M87 –, et pour la partie théorique, au néo-zélandais Roy Kerr (86 ans) qui a découvert en 1963 la solution exacte des équations de la relativité générale décrivant un trou noir en rotation (la situation astrophysique générique).

Voir ici la conférence plénière que l’équipe américaine de l’Event Horizon Telescope m’avait invité à donner en mai 2019 à l’Université de Harvard.

Entendons-nous bien, ceci n’est pas une critique du choix de l’Académie suédoise (qui par le passé a pu en effet se montrer contestable !)  : pour moi, nul autre physicien que Roger Penrose méritait davantage le prix théorique. Pour la partie observationnelle, le choix de Genzel et Ghez – dont les travaux de longue haleine exclusivement centrés sur la traque du putatif trou noir galactique Sagittarius A* font référence – me semble plus diplomatique, voire « politiquement correct », car partagé d’une part entre deux équipes, l’une européenne avec Genzel, l’autre américaine avec Ghez, qui se sont livrées une féroce concurrence, partagé d’autre part entre représentants des deux sexes, une équitabilité bien dans l’air du temps, devenue incontournable dans tous les secteurs de l’activité humaine .

Cette réaction « à chaud » une fois donnée,  je vais décrire de façon plus développée les travaux respectifs de Penrose (ici), puis de Genzel et Ghez (dans un autre billet). Il me suffit pour cela de reprendre en grande partie quelques « bonnes feuilles » de mes nombreux écrits sur le sujet. Dans mon tout neuf « L’écume de l’espace-temps », qui paraît le 14 octobre 2020, je ne cesse de rendre hommage aux géniales et très diverses contributions de Roger Penrose aussi bien à la théorie de la relativité générale, qu’à la physique des trous noirs, à la cosmologie, aux mathématiques pures et même aux sciences cognitives ! Quant à mon « Destin de l’Univers : trous noirs et énergie sombre » de 2006, il consacre un chapitre détaillé aux observations de Sagittarius A* au Centre Galactique, tandis que les plus récentes observations sont résumées dans mon article de 2019 pour l’Encyclopædia Universalis.


Allons-y! Et à tout seigneur tout honneur, commençons avec Roger Penrose. Il est l’un des esprits les plus puissants que j’aie jamais rencontrés, d’autant qu’il montre encore aujourd’hui, à l’âge de 89 ans, une exceptionnelle créativité.

« Sir » Roger Penrose (il a été anobli en 1994 par la reine d’Angleterre pour services rendus à la science) a profondément contribué au renouveau de la relativité générale pendant les années 1960 et 1970, en faisant usage des concepts et méthodes de la physique mathématique développées par l’école de Cambridge. Créée par Dennis Sciama (1926-1999) au début des années 1960, cette école a compté parmi ses plus remarquables représentants Roger Penrose (né en 1931), George Ellis (né en 1939), Stephen Hawking (1942-2018) et Brandon Carter (né en 1942), qui deviendra en 1976 mon directeur de thèse. Ces méthodes permettent notamment de traiter de manière originale des sujets comme la structure globale de l’espace-temps, les propriétés des trous noirs et les singularités inhérentes à la théorie de la relativité générale, sans qu’il soit nécessaire de résoudre les équations du champ d’Einstein.

L’école de Cambridge de physique mathématique. De gauche à droite : Dennis Sciama, Roger Penrose, Stephen Hawking, Brandon Carter et George Ellis

La relativité générale prédit que les étoiles très massives s’effondrent sur elles-mêmes sans limite. Leur champ gravitationnel devient alors si grand qu’il emprisonne la matière et la lumière à l’intérieur d’un trou noir, zone de non-retour délimitée par une surface appelée « horizon des événements ». En 1965, Roger Penrose démontra qu’au-delà de l’horizon, l’effondrement gravitationnel doit inévitablement se poursuivre pour atteindre un stade « singulier » où la densité devient infinie. C’est essentiellement à ce travail que fait référence le communiqué du prix Nobel. Continuer la lecture →

Actualités, Arts, Littérature, Musique, Roman

Hommage à Baptiste-Marrey (1928-2019)

22 commentaires

Baptiste-Marrey, très grand écrivain de langue française, vient de nous quitter le 22 janvier 2019 à l’âge de 91 ans. Pratiquement inconnu du public, ignoré par une critique littéraire germanopratine souvent mafieuse qui, pour l’essentiel, ne fait l’éloge que d’indigents écrivaillons, ce romancier, essayiste, poète et « agitateur culturel » était mon voisin à la campagne en même temps qu’une connaissance proche et amicale.

Hommage à l’homme et à son œuvre.

Il y a une vingtaine d’années je suis devenu propriétaire d’une petite fermette dans le village de Chevillon, dans le Nord de l’Yonne. J’allais y passer mes fins de semaine et une partie des vacances d’été, essentiellement pour retaper une à une les pièces de ma longère, entretenir mon jardin et mes arbres fruitiers, faire les confitures d’automne et cultiver mon potager. Un jour le facteur, qui avait appris que j’étais chercheur et que j’avais publié quelques livres, me dit « vous savez que vous avez un voisin écrivain, comme vous ? ». Sur le moment j’ai cru qu’il faisait allusion à mon collègue astrophysicien et ami Hubert Reeves. Il n’était pas précisément mon voisin à Chevillon, mais sa belle propriété de Malicorne, où je me rendais régulièrement, n’est située qu’à une dizaine de kilomètres – ce qui, dans les vastes campagnes de cette région, s’apparente à un proche voisinage. Je ne prêtai donc guère attention à l’information, et quelques années passèrent sans plus de curiosité de ma part.

C’est alors qu’un samedi de printemps 2005, au matin, on frappa à la porte de ma longère. Un homme de petite taille, légèrement corpulent, l’air affable, se tenait devant le seuil. Il se présenta à peu près ainsi  : « Bonjour, je suis votre voisin, j’habite une maison à 500 mètres en haut de la rue. Je suis écrivain, je viens vous saluer pour faire votre connaissance. Je m’appelle Baptiste Marrey ».

J’avoue que je n’avais jamais entendu parler d’un écrivain nommé ainsi, et sur le moment j’ai pensé qu’il s’agissait probablement d’un de ces petits auteurs régionalistes dont la littérature, ancrée dans le terroir, reste généralement ignorée en dehors de leur province. Mais lorsque, par politesse, je lui demandai chez quel éditeur il avait publié et qu’il me répondit Actes Sud, je me dis que cette prestigieuse et exigeante maison d’édition ne pouvait avoir dans son catalogue un auteur de seconde zone, de sorte que ma curiosité fut enfin éveillée.

C’est ainsi que je fis la connaissance de Baptiste-Marrey – de son vrai prénom Jean-Claude — et de son épouse, la comédienne Alix Romero. Vivant à Gentilly, ils possédaient en bordure du village de Chevillon, à moins d’un kilomètre de chez moi, une très belle demeure de campagne, « La Marelle », bien mieux entretenue que ma très rustique longère. Nous commençâmes donc à nous fréquenter, échangeant naturellement quelques-uns de nos écrits respectifs.

Je dois dire que je ne m’attendais pas du tout au choc littéraire que j’éprouvai en lisant en 2006 le premier roman qu’il m’offrit : Les papiers de Walter Jonas. Un vrai chef-d’œuvre, sur lequel je reviendrai plus bas.

Plus tard il me fit présent d’autres titres, que je dévorai comme le premier : SMS, Elvira, Edda H, consacrés à la musique classique et à l’opéra, passions communes, et l’Atelier de Peter Loewen, autre chef-d’œuvre cette fois consacré à la peinture (j’eus plus tard l’occasion de rencontrer l’un de ses fils, l’excellent peintre Gilles Marrey, et d’en visiter une superbe exposition au Musée de Sens).

Pour en savoir plus sur le parcours de Baptiste-Marrey je renvoie le lecteur intéressé au bel article qui lui est consacré sur Wikipédia, assorti d’une bibliographie assez complète (douze romans, une vingtaine d’essais). En résumé, il est né à Paris, dans le quartier de Bercy, et y a passé ses jeunes années. « La peau de mon enfance », l’un de ses derniers ouvrages publié en 2016, est un pèlerinage bouleversant dans le territoire de son enfance irrémédiablement défiguré par l’urbanisation du quartier: “Pierre à pierre me fut arrachée la peau de mon enfance. De cette ville-là (Paris), il ne reste rien que je puisse montrer à mes propres enfants.” … Continuer la lecture →

Actualités, Astronomie, Histoire des sciences

Les Léonides, pluie céleste de novembre (2/2)

4 commentaires
Suite du précédent billet

Dans les nuits d’automne, errant par la ville,
Je regarde au ciel avec mon désir,
Car si, dans le temps qu’une étoile file,
On forme un souhait, il doit s’accomplir.
François Coppée, Etoiles Filantes (1877)

Fontaine de flammèches et d’éclairs illuminant l’atmosphère durant la pluie de 1833.
Nom de baptème

Lors de la pluie de novembre 1833, les nombreux observateurs de la côte Est des Etats-Unis et de la région des Chutes du Niagara avaient vu les météores semblant provenir de la constellation du Lion (Leo). Le nom de Léonides fut alors donné à cet essaim.

A la mi-novembre 1799, un phénomène similaire à la pluie de 1833 avait déjà été observé au large des côtes du Vénézuela par le célèbre naturaliste allemand Alexander von Humboldt, en compagnie du botaniste français Aimé Bonpland (1773-1858) [deux jours après ils partirent explorer le fleuve Orénoque].

Gravure extraite du célèbre ouvrage de Humboldt “Cosmos. Essai d’une description physique du Monde, 1847-1859.
Hubert Anson Newton (1830-1896).  Son travail d’archives  sur les Léonides a été repris en 1958 par Susumu Imoto et Ichiro Hasegawa pour les textes anciens chinois, japonais et coréens, puis par Gary Kronk en 1988 et Donald Yeomans en 1991, qui ont dressé des catalogues descriptifs de toutes les pluies de Léonides observées, de l’an 901 jusqu’à nos jours.

Hubert Anson Newton, autre professeur de Yale, subodora donc une périodicité du phénomène. Il rechercha dans les chroniques astronomiques anciennes des allusions aux « météores de novembre ». Il en trouva treize mentions, allant de l’an 901 à 1833. Newton en déduisit une périodicité de 33 ans un quart, et en 1864 il prédit une grande nuit des Léonides pour novembre 1866, année du passage suivant. Sa prédiction fut vérifiée. En novembre 1866, des centaines de météores à la minute furent bel et bien observés partout en Europe, et de nombreux compte-rendus parurent dans les journaux.

On en vit encore en 1867 et 1868, quoique à un rythme moindre. De remarquables gravures de l’époque en attestent, comme celles du génial dessinateur et astronome de l’Observatoire de Paris Etienne-Leopold Trouvelot et celle figurant dans un bel ouvrage d’astronomie populaire d’Emmanuel Liais. [Ce dernier, expulsé de lʼObservatoire de Paris en 1858 par son irascible directeur Urbain Le Verrier, avait poursuivi sa carrière au Brésil].

A gauche, dessin de Trouvelot. A droite, deux gravures extraites de l’ouvrage publié par Liais en 1881, “L’espace céleste, ou, Description de l’univers”.
La comète Tempel-Tuttle, maman des Léonides

Restait à trouver la cause du phénomène. Le voile fut levé par la découverte d’une comète de magnitude 6 nommée Tempel-Tuttle, en hommage à ses deux découvreurs, Ernst Tempel et Horace Tuttle. Le premier la détecta le 19 décembre 1865, le second quelques jours plus tard, le 6 janvier 1866. Cette même année, l’Italien Giovanni Schiaparelli démontrait que l’orbite de cette comète était quasiment identique à celle qu’occupent les particules provoquant l’essaim des Léonides, faisant pour la première fois le lien qui manquait. Continuer la lecture →

Actualités, Astronomie, Histoire des sciences

Les Léonides, pluie céleste de novembre (1/2)

Un commentaire

Une étoile filante brille
Et tout tombe
                   Le ciel se ride
Les bras s’ouvrent
                   Et rien ne vient
Un cœur bat encore dans le vide

Pierre Reverdy :  Etoile filante (extrait),
dans Plupart du temps, 1915-1922.

Le mois de novembre est propice aux pluies d’étoiles filantes, appelées aussi essaims météoritiques. Trois d’entre eux connaîtront leur maximum d’activité. L’essaim météoritique des Taurides Nord, actif du 20 Octobre au 10 Décembre, aura son maximum le 12 novembre, avec un taux moyen de 5 météores à l’heure. L’essaim des alpha-Monocérotides est actif du 15 au 25 Novembre avec un maximum le 21 Novembre ; son activité est très variable d’une année à l’autre, pouvant monter à 400 météores à l’heure durant environ 30 minutes. Mais c’est surtout l’essaim des Léonides qui attirera l’attention. Actif du 6 au 30 Novembre, il atteindra son maximum le 17 avec un taux d’environ 15 à l’heure. Cela paraît modeste, mais comme on va le voir, au cours de certaines années passées ce taux a atteint le taux phénoménal  de 200 000 à l’heure. Ce n’était plus une pluie, mais une tempête!

Belle pluie des Orionides vue depuis la Mongolie intérieure

Avant de revenir sur ces pluies historiques qui ont marqué les mémoires, quelques petits rappels astronomiques s’imposent.

Éphémère progéniture de comète

Les belles mais fugitives étoiles filantes sont des grains cométaires microscopiques qui, en pénétrant dans l’atmosphère, s’échauffent par frottement. Leur température monte à 3 000° C, et elles se consument dans la haute atmosphère, à 80 km d’altitude, créant ces traînées lumineuses qui ne durent souvent qu’une fraction de seconde. En fait, ce n’est pas la combustion du grain porté à blanc que l’on voit à si grande distance, mais la traînée d’ionisation qu’il laisse dans l’atmosphère. Ces étincelles nomades sont la version miniaturisée et anodine des météores – le bonzaï du bolide ! Leur taille ne dépasse pas quelques millimètres. Ce sont des silicates analogues à des grains de sable.

Un bolide

Il existe un lien entre la masse du grain et sa luminosité, donné par une formule dite de Hughes. A la vitesse typique de 70 km par seconde, cela donne une luminosité égale à celle d’une étoile de première grandeur comme Sirius pour un grain de seulement 3 millimètres, et une intensité tout juste visible à l’œil nu pour un grain de 0,3 millimètre.

Pour que nous puissions voir une si petite poussière à 80 km de distance, il faut qu’elle ait mis toutes ses forces dans la bataille. Parler de chant du cygne n’est rien. Il faudrait parler de la flambée de l’étoile filante. Les scientifiques se contentent de dire que « le rendement de la combustion est très élevé ».

Un grain cométaire

Lorsque, par une nuit quelconque, vous observez une étoile filante, il s’agit d’un météore sporadique. Par ciel dégagé, on peut en voir quelques-uns par heure, en principe davantage après minuit qu’avant, et davantage en automne qu’au printemps (pour l’hémisphère nord).

Si de nombreux météores apparaissent la même nuit et semblent provenir du même endroit du ciel, il s’agit d’une pluie d’étoiles filantes. On verra alors dix, voire cinquante météores et plus par heure, dans un ciel sombre sans Lune, loin des lumières des villes.

Cet essaim de météores résulte du passage annuel de la Terre dans la traînée de poussières laissée par une comète. Dans sa course folle, l’astre vagabond véhicule et éjecte autour de lui une grande quantité de matière, allant de la poussière au caillou. Une traînée composée de myriades de particules jalonne sa trajectoire elliptique dans le vide interplanétaire.

Ces sillages remplis de grains s’étendent sur des centaines de millions de kilomètres pour quelques dizaines de milliers de kilomètres de largeur, ce qui leur confère une forme de tube tordu.

Les poussières flottent dans ce tube, obscures, et la Terre, en les bousculant de son atmosphère, les enflamme. Dans un certain sens, c’est plutôt la Terre qui tombe sur elles qu’elles sur nous. Si ce n’est que notre planète, en croisant un tube, agit comme un aspirateur gravitationnel et engloutit ce qui traîne à la ronde.

Durant les plus belles pluies météoritiques annuelles on peut voir jusqu’à cent météores à l’heure. Et beaucoup plus encore lors de certaines années exceptionnelles – les grands crus -, où l’événement prend l’allure d’une véritable tempête. Continuer la lecture →

Actualités, Astronomie, Histoire des sciences, Sciences

L’éclipse lunaire du siècle

11 commentaires

Ce vendredi 27 juillet, une éclipse de Lune sera visible en France métropolitaine dès le crépuscule, soit à partir de 21h dans le sud de la France pour ceux qui auront la possibilité d’observer l’astre des nuits dès son émergence sur l’horizon. Pour les autres le spectacle sera décalé de quelques minutes.

Avec une durée de totalité de 1 h 42 min et 57 s, proche du maximum possible de 1 h 47 min, ce sera la plus longue éclipse de Lune du XXIe siècle ! Un événement à ne pas rater, dont vous trouverez une description précise dans cet article de Xavier Demeersman sur Futurascience.

Je reproduis ici une carte de cette éclipse déjà publiée il y a près de vingt ans dans mon livre « Eclipses, les rendez-vous célestes » (Bordas, 1999) en collaboration avec l’ami Serge Brunier.

L’éclipse de Lune totale et centrale du 27 juillet 2018 sera au zénith de Madagascar, de l’ïle de la Réunion et de l’Ile Maurice, mais elle sera aussi visible en totalité ou en partie en Europe, en Afrique, en Asie et en Australasie.

Lors d’une précédente éclipse totale de Lune (28 septembre 2015), j’avais déjà posté sur ce blog un billet assez développé sur les éclipses de Lune qui ont marqué l’histoire des hommes et des civilisations. Je vous invite à lire ou relire ces éclipses de lune mémorables. Et si le sujet vous passionne, pourquoi ne pas relire également les deux billets de mars 2015 que j’avais consacrés aux éclipses dans la littérature !

Pour honorer la présente éclipse du 27 juillet 2018, j’ajoute quelques compléments de mon cru d’ordre historique et pratique, adaptés de mon livre.

Empêchements et défaillances

Dans les Institutions astronomiques, premier livre d’astronomie rédigé en français et publié en 1557, le poète et savant Jean-Pierre de Mesmes (1516-1578), proche de la Pléiade, a proposé un vocabulaire scientifique emprunté à la langue vulgaire au lieu du grec et du latin. Il suggérait d’appeler “empêchements” les éclipses de Soleil et “défaillances” les éclipses de Lune. Si ces termes poétiques n’ont pas été adoptés, ils marquent bien la différence essentielle entre les deux phénomènes.

Bien que toute éclipse soit causée par l’interception d’un astre – la Lune ou la Terre- devant le Soleil, les éclipses solaires et lunaires diffèrent en effet sur plusieurs points. Dans une éclipse solaire, la Lune masque le Soleil en totalité ou en partie, mais seulement pour certains points de la surface de la Terre : ici, le long d’une bande longue et étroite, elle est totale ou annulaire ; là, elle n’est que partielle, et la partie cachée du Soleil est plus ou moins grande ; ailleurs, on ne voit nulle trace d’éclipse. Dans une éclipse lunaire, au contraire, notre satellite cesse en totalité ou en partie d’être éclairé par le Soleil parce qu’il traverse l’ombre de la Terre, et cet aspect de la Lune est le même pour tous les habitants de l’hémisphère terrestre qui ont la Lune au-dessus de l’horizon.

Quoi qu’il en soit, les éclipses mettent en scène ces trois acteurs aux rôles bien distincts que sont la Terre, le Soleil et la Lune. Une éclipse de Soleil se produit quand la Lune passe devant le Soleil au moment de la nouvelle lune, une éclipse de Lune se produit quand la Lune passe dans l’ombre de la Terre au moment de la pleine lune. Dans les deux configurations, les trois corps sont alignés.

Une éclipse de Lune est visible en tout point de la Terre où la Lune est au-dessus de l’horizon. Au contraire, une éclipse de Soleil n’est visible que dans une zone de la Terre relativement réduite. Ces schémas sont extraits d’un atlas du XVIIIe siècle.
Claude Buy de Mornas. Atlas méthodique et élémentaire de géographie. Paris 1761.

Continuer la lecture →

Actualités, Astronomie

30 juin, Journée de l’astéroïde

21 commentaires

Le 6 décembre 2016, l’Assemblée générale des Nations Unies a adopté une résolution déclarant le 30 juin Journée internationale des astéroïdes « afin de commémorer chaque année, au niveau international, l’anniversaire de l’explosion de Tunguska (Sibérie, Fédération de Russie) survenue le 30 juin 1908 et de sensibiliser la population aux risques d’impact d’astéroïdes. »

La Journée internationale de l’astéroïde (Asteroid Day) vise à sensibiliser le grand public aux menaces que représentent les astéroïdes, l’informer des mesures qui seraient prises pour assurer la communication de crise au niveau mondial en cas de risques liés aux géocroiseurs, mais aussi (et surtout) à mieux connaître ces fascinants résidus de la formation du système solaire.

Retour sur l’événement du 30 juin 1908, à partir d’extraits de mon livre paru en 2012, « Astéroïdes, la Terre en danger »

Le 30 juin 1908 à 7 h du matin, une effroyable explosion ravage la Tunguska, lointaine vallée pratiquement inhabitée qui étend ses forêts de conifères entre la ville d’Omsk et le lac Baïkal, en Sibérie occidentale. Accompagné d’une lueur aveuglante, le souffle couche au sol tous les arbres dans un cercle de cent kilomètres, décime des milliers de rennes, se propage, atteint les villages, brise des vitres, ébranle des immeubles. La déflagration est entendue à 1500 km à la ronde, jusqu’au cercle arctique.

Un habitant de Vanarava, à 60 km de l’endroit, aperçoit juste avant l’explosion un objet énorme et étincelant, gros comme la moitié du Soleil, fendre le ciel à la vitesse de l’éclair. Suivi par un sillage de poussière et de fumée, l’objet dégage une chaleur telle que la chemise de l’homme commence à prendre feu. Terrorisé, il a juste le temps de courir se réfugier dans sa maison afin d’éteindre les flammes.

D’autres témoins affirment avoir vu s’élever un énorme champignon de fumée noire coupant le ciel en deux. Vingt kilomètres au nord de Varanava, les nomades des tribus Tungouzes transhumant dans les forêts croient que la fin du monde est venue.Leurs huttes, arrachées du sol comme des fétus de paille, s’envolent aux quatre vents, et ils perdent des centaines de leurs rennes, gravement brûlés.

Région parmi les plus hostiles, la Tunguska compte alors très peu d’habitants. Si les dégâts matériels sont énormes, on ne déplore heureusement que quelques blessés et brûlés. Un vrai miracle. D’autant que d’incroyables phénomènes lumineux se produisent. Ce soir-là, la nuit ne se couche pas dans presque toute l’Europe. La Grande-Bretagne est éblouie par un coucher de Soleil étincelant ; la nuit, sillonnée de nuages de lumière rose, est si claire que les Londoniens peuvent lire leur journal dans la rue à minuit, sans avoir recours à l’éclairage de la ville. Des nuits d’une blancheur irréelle s’installent plusieurs semaines durant.

Enregistrée par les sismographes du monde entier, l’énergie libérée est estimée à 15 millions de tonnes de TNT. C’est mille fois la bombe atomique qui détruira 37 ans plus tard Hiroshima.

Du fait des événements qui secouent le début du siècle (purge politique en Russie, Première Guerre mondiale), les savants soviétiques ne commencent à explorer le site de la Tunguska qu’en 1927. Les arbres sont encore brûlés, couchés radialement autour du centre de l’explosion.

Continuer la lecture →

Actualités, Sciences

Stephen Hawking (1942-2018) : ses travaux

33 commentaires

Complément au billet précédent Stephen Hawking (1942-2018) : Souvenirs personnels

Les travaux de Stephen Hawking tournent essentiellement autour d’une interrogation aussi vieille que l’humanité : l’éternité du temps. Pour tenter d’y répondre de façon pertinente, le physicien britannique  a utilisé l’arsenal de la physique contemporaine : la relativité générale (théorie de la gravitation), la mécanique quantique (théorie des particules élémentaires et de leurs interactions) et le problématique mariage des deux (la gravitation quantique), concentrant sa stratégie sur deux domaines clés de la recherche théorique : les trous noirs et la cosmologie.

La relativité générale prédit que les étoiles très massives s’effondrent sur elles-mêmes sans limite. Leur champ gravitationnel devient alors si grand qu’il emprisonne la matière et la lumière à l’intérieur d’un « trou noir », zone de non-retour délimitée par une surface appelée horizon des événements. À la fin des années 1960, Hawking et son mentor Roger Penrose ont démontré qu’au-delà de l’horizon, l’effondrement gravitationnel doit inévitablement se poursuivre pour atteindre un stade « singulier » où la densité devient infinie. A la question « le temps a-t-il une fin ? », la réponse est donc oui dans le cadre de la relativité générale classique : le futur s’arrête aux singularités cachées au fond des trous noirs.

On doit à Roger Penrose (né en 1931) de nombreuses contributions à la physique des trous noirs, à la cosmologie et aux mathématiques.

Hawking s’est ensuite attaché, en collaboration avec d’autres chercheurs, à la mise en place d’une « thermodynamique des trous noirs » calquée sur les lois de la thermodynamique usuelle, autrement dit à les modéliser comme des systèmes physiques capables d’interagir avec le milieu extérieur et d’évoluer au cours du temps. Hawking a notamment démontré la loi de croissance irréversible de l’aire d’un trou noir, qui peut être mise en parallèle avec la loi de croissance de l’entropie. En outre, la gravité de surface d’un trou noir doit jouer le rôle d’une température. Un paradoxe, pointé par Jacob Bekenstein de l’Université de Princeton, surgit alors : si le trou noir possède réellement une température et une entropie, il doit être capable de rayonner de l’énergie, ce qui entre en conflit avec sa définition classique.

En 1970, Stephen Hawking et le physicien grec Demetrios Christodolou ont démontré qu’au cours de son évolution, un trou noir ne peut qu’accroître sa surface. Si deux trous noirs entrent en collision, ils forment un seul trou noir dont la surface A3 est plus grande que la somme des surfaces A1 et A2 des trous noirs parents.

Le dilemme a été résolu en 1974 par Hawking (un peu par hasard a-t-il plus tard reconnu), lorsqu’il a entrepris d’étudier l’interaction d’un trou noir avec le vide quantique. Dans la conception classique du trou noir, rien ne peut sortir de l’horizon. En mécanique quantique, au contraire, en raison du principe d’incertitude, une particule a toujours une probabilité non nulle de franchir une barrière de potentiel par effet tunnel. Appliqué à la théorie des trous noirs microscopiques, le principe d’incertitude crée des sortes de « tunnels quantiques » à travers l’horizon gravitationnellement infranchissable, permettant à des particules de s’en échapper et au trou noir de s’évaporer. Cette évaporation quantique du trou noir se manifeste sous forme d’un rayonnement dont la température est bien fixée par la gravité régnant à la surface du trou noir.

Une explication de l’évaporation d’un micro trou noir par polarisation du vide quantique.

L’évaporation quantique est totalement négligeable pour les trous noirs astrophysiques de masse stellaire ou galactique, lesquels s’accroissent au cours du temps, mais Hawking a montré qu’elle deviendrait dominante pour les « mini-trous noirs » de la taille d’un proton et moins massifs qu’un milliard de tonnes, leur temps d’évaporation devenant plus court que l’âge de l’univers (quatorze milliards d’années). De tels objets auraient pu se former au cours du Big Bang, lorsque la densité d’énergie ambiante était si élevée que la moindre fluctuation aurait pu se condenser en trou noir microscopique.

Cette découverte théorique du rayonnement quantique des trous noirs – appelé depuis « rayonnement Hawking » – a permis de comprendre que les trous noirs, outre leur intérêt astrophysique, jouent le rôle d’une pierre de Rosette dans le déchiffrage des liens énigmatiques entre gravité, quantas et thermodynamique. C’est à ce titre qu’elle restera la contribution la plus importante de Hawking à la physique théorique moderne. Continuer la lecture →

Actualités, Astronomie, Sciences

Stephen Hawking (1942-2018) : Souvenirs personnels

8 commentaires
Stephen Hawking (8 janvier 1942-14 mars 2018) rappelait souvent avec malice qu’il était né 300 ans jour pour jour après la mort de Galilée. Il ne se doutait probablement pas qu’il mourrait un 14 mars, jour anniversaire de la naissance d’Albert Einstein. Cette belle photo le montre à la fin des années 1970 en compagnie de son épouse Jane et deux de ses enfants.

 

Mon premier contact avec les travaux de Stephen Hawking remonte à 1975, année où j’ai quitté mes études de mathématiques pures à l’Université de Marseille pour suivre un D.E.A. de physique théorique et de cosmologie à la faculté de Montpellier sous la direction du professeur Andrillat. De fait je n’ai guère fréquenté les cours, car durant les précédentes vacances d’été j’avais déjà lu et assimilé l’excellente monographie sur la relativité générale et la cosmologie qu’Andrillat avait publiée en 1970. Du coup, j’ai pris l’initiative de me lancer dans la lecture de deux tout nouveaux ouvrages de haut vol parus en 1973 : The large scale structure of space-time de Stephen Hawking et George Ellis, et Gravitation de Charles Misner, Kip Thorne et John Wheeler. Ces livres émanant des deux grandes écoles anglo-saxonnes de physique théorique de l’époque, celle de Cambridge en Angleterre et celle de Princeton aux Etats-Unis,  allaient vite devenir de vraies bibles de la discipline, en  traitant la théorie d’Einstein selon des angles différents mais complémentaires.

Si la partie technique de ces livres était trop ardue pour ma formation de l’époque, j’en avais quand même retiré un immense intérêt pour les méthodes de physique mathématique développées par l’école de Cambridge, créée par Dennis Sciama dans les années 1960 et dont les plus remarquables disciples étaient Roger Penrose, Stephen Hawking, Brandon Carter et George Ellis. Ces méthodes permettaient notamment de traiter de manière originale des sujets comme la structure globale de l’espace-temps, les propriétés des trous noirs et les singularités inhérentes à la théorie de la relativité générale.

De gauche à droite : Dennis Sciama (1926-1999), Roger Penrose (né en 1931), Stephen Hawking (1942-2018), Brandon Carter (né en 1942) et George Ellis (né en 1939)

A la fin de cette année de DEA j’ai d’ailleurs rédigé un gros mémoire intitulé « Groupes d’isométries en relativité générale ». C’était en fait de la pure « géométrie différentielle » appliquée à la théorie gravitationnelle d’Einstein, directement inspirée par la lecture du livre de Hawking et Ellis. C’est alors que le professeur Andrillat m’a vivement conseillé d’aller poursuivre mes études à l’Observatoire de Paris-Meudon, où existait depuis peu un « Groupe d’astrophysique relativiste ». Recruté par le CNRS, Brandon Carter venait de quitter Cambridge pour en prendre la direction, et il sut faire confiance au jeune étudiant enthousiaste que j’étais. Collègue et ami personnel de Stephen Hawking, il m’a dirigé vers un sujet de thèse riche mais complexe concernant les singularités qui apparaissent dans certains modèles de la cosmologie relativiste. C’est ainsi que l’on désigne les points de l’espace-temps où certains paramètres physiques deviennent infinis. Le centre des trous noirs est une singularité de l’espace-temps, un point où la gravité devient infinie, ainsi que le début de l’Univers tel qu’il est décrit par la théorie du Big Bang. Par essence, on ne peut appréhender les singularités avec les outils de l’astrophysique, seulement avec ceux de la physique mathématique. Hawking et Penrose avaient justement démontré l’occurrence inévitable de singularités en relativité générale, moyennant quelques hypothèses plausibles. Ce sujet me convenait parfaitement !

Au bout d’un an, j’ai obtenu une bourse du British Council me permettant d’aller travailler trois mois à l’université de Cambridge, dans le laboratoire de Stephen Hawking. Il était déjà connu dans le petit monde des physiciens mais sans plus, et j’étais très impressionné d’avoir un bureau au DAMTP (Department of Applied Mathematics and Theoretical Physics), laboratoire prestigieux situé à l’époque dans une ancienne usine reconvertie, rue Silver Street. Encore plus impressionné le premier jour où, assistant à un séminaire au DAMTP, j’ai vu arriver Stephen Hawking en fauteuil roulant, la tête inclinée de côté, rictus sur le visage mais le regard toujours extraordinairement vif.

Le D.A.M.T.P. dans ses anciens locaux de Silver Street, avant son déménagement en 2002 dans des bâtiments modernes.

Dans les mois qui ont suivi j’ai eu l’occasion de mieux connaître Stephen. Je me souviens notamment d’un repas à la cantine de l’université, montrant les extraordinaires difficultés auxquelles Stephen était en permanence confronté pour accomplir les actes les plus simples de l’existence. Je me souviens aussi du jour où, voulant assister à un séminaire se tenant loin du DAMTP et nécessitant un déplacement en voiture, Stephen avait demandé si je pouvais le conduire avec mon propre véhicule. Je l’avais donc soulevé de son fauteuil roulant et pris dans mes bras pour le déposer sur le siège avant, m’étonnant de son poids qui ne devait guère dépasser les 40 kilos. Mais mon incapacité à communiquer vraiment avec lui était embarrassante. A cette époque en effet son élocution était déjà fortement altérée par sa maladie, de sorte que seules les personnes le connaissant très bien pouvaient comprendre ses paroles, ce qui pouvait créer des malentendus. Continuer la lecture →

Actualités, Astronomie

Eclipses intellectuelles

13 commentaires

Ceci est, inhabituellement chez moi, un petit billet d’humeur. Je m’y élève  avec quelque retard contre les égarements de certains technocrates de l’éducation nationale. Ils sont si nombreux, ces égarements,  que je n’en citerai qu’un ici.  La scène s’est déroulée en mai dernier, lorsque fut annoncé un passage de Mercure devant le Soleil se produisant le 9 de ce mois, événement astronomique intéressant et pouvant faire l’objet d’activités ludiques,  pédagogiques – et donc instructives – pour nos chères têtes blondes, brunes ou rousses. J’y ai d’ailleurs à l’époque consacré deux billets sur ce même blog, ici et là.

Or, j’avais appris qu’une certain directeur académique des services de l’Éducation nationale pour la Haute Garonne, serviteur zélé du Ministère de la Déséducation Nationale, avait donné pour directive aux enseignants de garder les enfants en classe durant tout la durée du phénomène, par mesure de précaution cf. cette circulaire.

Le même genre de recommandation aberrante  émanant “d’en haut” – accompagnée d’un texte en tous points semblable – avait déjà été préconisée lors d’une éclipse solaire en  2015, et répercutée dans de nombreuses académies (dont celle de Nice) .

De nombreuses associations s’étaient élevées contre ce type de directives. Pour ma part, mon sang n’ayant fait qu’un tour, voici la lettre que j’avais illico adressée à ce gardien de l’ordre. Lettre évidemment restée sans réponse… Continuer la lecture →

Actualités, Astronomie, Poésie

Le Météore du 13 Août

Un commentaire

« A la seconde où tu m’apparus, mon cœur eut tout le ciel pour l’éclairer. Il fut midi à mon poème. Je sus que l’angoisse dormait.»
René Char : Le Météore du 13 Août (Fureur et Mystère,  1948).

Des dizaines d’excellents billets de blog ici et là sont consacrés à l’actualité des Perséides, cette pluie d’étoiles filantes qui illumine chaque année le ciel de la mi-août. Pour ne pas faire redondance, je me contenterai ici de quelques notes astronomico-poétiques.

Comme chacun sait (ou devrait savoir), ces belles mais fugitives étincelles nomades sont des grains cométaires microscopiques qui, en pénétrant dans l’atmosphère, s’échauffent par frottement. Leur température monte à trois mille degrés, et elles se consument dans la haute atmosphère, à quatre-vingts kilomètres d’altitude environ, créant ces traînées lumineuses qui ne durent souvent qu’une fraction de seconde. En fait, ce n’est pas la combustion du grain porté à blanc que l’on voit à si grande distance, mais la traînée d’ionisation qu’il laisse dans l’atmosphère. Les étoiles filantes sont la version miniaturisée et anodine des météores, le « bonzaï » du bolide.

Les étoiles filantes, si elles ne font pas d’argent ni ne répondent aux vœux, font parfois de beaux  poèmes:

A la pointe où se balance un mouchoir blanc
Au fond noir qui finit le monde
Devant nos yeux un petit espace
Tout ce qu’on ne voit pas
Et qui passe
Le soleil donne un peu de feu

Une étoile filante brille
Et tout tombe
Le ciel se ride
Les bras s’ouvrent
Et rien ne vient
Un cœur bat encore dans le vide
Un soupir douloureux s’achève
Dans les plis du rideau le jour se lève

Pierre Reverdy, Etoile filante (dans Plupart du temps, 1915-1922)

Leur taille ne dépasse pas quelques millimètres. Ce sont des silicates, analogues à des grains de sable. La luminosité des grains est fonction de leur masse. À la vitesse typique de soixante-dix kilomètres par seconde, un grain de seulement trois millimètres présente une luminosité égale à celle d’une étoile de première grandeur comme Sirius, mais pour un grain caractéristique d’un tiers de millimètre, l’intensité est tout juste visible à l’œil nu.

meteore_bolideLorsque, par une nuit quelconque, vous observez une étoile filante, il s’agit d’un météore sporadique. Par ciel dégagé, on peut en voir quelques-uns par heure, en principe davantage après minuit qu’avant, et davantage en automne qu’au printemps – du moins pour l’hémisphère nord.

Si de nombreux météores apparaissent la même nuit et semblent provenir du même endroit du ciel, il s’agit d’une pluie d’étoiles filantes. On voit alors dix, voire cinquante météores et plus par heure, dans un ciel sombre sans Lune et loin des lumières des villes. Continuer la lecture →

Actualités, Mes publications, Sciences

L’univers holographique (2) : La gravité quantique façon théorie des cordes

10 commentaires

Suite du billet précédent L’univers holographique (1) : le paradoxe de l’information

Le paradoxe de l’information lié aux trous noirs reflète notre incapacité actuelle à élaborer une théorie cohérente de la gravité quantique. L’approximation semi-classique de Hawking cesse d’être valide quand le trou noir devient suffisamment petit pour que le rayon de courbure à l’horizon des événements atteigne la longueur de Planck, 10-33 cm, autrement dit lorsque non seulement la matière et l’énergie, mais aussi le champ gravitationnel doivent être quantifiés. La description finale de l’évaporation et la restitution partielle ou complète de l’information exigent donc un traitement complet en gravité quantique, branche fondamentale de la physique qui cherche à décrire la gravitation en utilisant les principes de la mécanique quantique.

Richard Feynman (1918-1988), prix Nobel de physique 1965, auteur des diagrammes du même nom.
Richard Feynman (1918-1988), prix Nobel de physique 1965, auteur des diagrammes du même nom.

L’application de la mécanique quantique aux objets physiques tels que le champ électromagnétique, qui s’étendent dans l’espace et le temps, a connu un succès éclatant avec la théorie quantique des champs[1]. Celle-ci forme la base de la compréhension du modèle standard de la physique des particules élémentaires, rendant compte des interactions électromagnétiques, nucléaire forte et nucléaire faible. Elle permet de calculer les probabilités d’événements en utilisant les techniques de la théorie des perturbations. Les diagrammes de Feynman décrivent les chemins de particules ponctuelles et leurs interactions. Chaque diagramme représente une contribution à un processus d’interaction. Pour leurs calculs, les physiciens additionnent en premier lieu les contributions les plus fortes, puis les plus petites, et ainsi de suite, jusqu’à atteindre la précision désirée.

Diagramme de Feynman. Lorsque deux particules (ici deux électrons venant du bas) interagissent, elles peuvent le faire « simplement », en échangeant un seul photon (schéma du haut). Mais ce photon peut lui-même se matérialiser puis de dématérialiser en chemin. Sur le schéma du bas, par exemple, il crée une paire électron-positron qui recrée ensuite le photon. Si l’on tient compte de cette aventure, la description de l’interaction des deux électrons de départ n’est plus la même. Cela n’est en fait que la « première correction ». En effet, il peut arriver au photon des histoires beaucoup plus compliquées qui représentent des corrections d’ordre 2,3,4… La physique quantique exige de tenir compte de l’infinité de ces corrections pour le moindre calcul. Cette difficulté considérable a conduit à incorporer à la physique quantique l’idée de renormalisation.
Diagramme de Feynman. Lorsque deux particules (ici deux électrons venant du bas) interagissent, elles peuvent le faire « simplement », en échangeant un seul photon (schéma du haut). Mais ce photon peut lui-même se matérialiser puis de dématérialiser en chemin. Sur le schéma du bas, par exemple, il crée une paire électron-positron qui recrée ensuite le photon. Si l’on tient compte de cette aventure, la description de l’interaction des deux électrons de départ n’est plus la même. Cela n’est en fait que la « première correction ». En effet, il peut arriver au photon des histoires beaucoup plus compliquées qui représentent des corrections d’ordre 2,3,4… La physique quantique exige de tenir compte de l’infinité de ces corrections pour le moindre calcul. Cette difficulté considérable a conduit à incorporer à la physique quantique l’idée de renormalisation.

 

Mais ce procédé ne marche que si les contributions deviennent réellement négligeables à mesure qu’un plus grand nombre d’interactions est pris en compte. Lorsqu’il en va ainsi, la théorie est dite “faiblement couplée” et les calculs convergent vers des valeurs physiques finies. S’il en va différemment, la théorie est dite “fortement couplée” et les méthodes standard de la physique des particules échouent. C’est notamment ce qui arrive avec le graviton, supposé être la particule médiatrice du champ gravitationnel. Le graviton, créant de la masse-énergie, interagit avec lui-même, ce qui crée de nouveaux gravitons, qui à leur tour interagissent, et ainsi de suite, jusqu’à la divergence. L’échec de la technique des perturbations pour quantifier la gravité a donc conduit les physiciens à explorer d’autres voies. Continuer la lecture →

Actualités, Mes publications, Sciences

L’univers holographique (1) : le paradoxe de l’information

19 commentaires

Ce billet est le premier d’une série de 6 reprenant un article initialement publié en anglais dans la revue Inference : The International Review of Science, auquel j’ai rajouté des illustrations à caractère pédagogique.

Introduction

Lors d’un exposé donné le 25 août 2015 au KTH Royal Institute of Technology à Stockholm qui a fait l’objet d’un grand tapage médiatique, Stephen Hawking a annoncé avoir résolu un problème de la physique appelé paradoxe de l’information [1]. Ce dernier illustre un conflit potentiel entre la mécanique quantique et les modèles de trou noir décrits par la relativité générale ; à ce titre, il joue un rôle central en physique fondamentale et divise la communauté des théoriciens depuis quatre décennies. Selon Hawking, toute l’information sur la matière et l’énergie contenue dans le volume 3D du trou noir résiderait en réalité sur sa surface 2D, l’horizon des événements, codée sous forme d’hologramme.

hologram1
Un hologramme est une photographie d’un type particulier qui engendre une image tridimensionnelle quand on l’éclaire de façon appropriée ; toute l’information décrivant une scène en trois dimensions est encodée dans le motif de zones claires et sombres inscrit sur un film à deux dimensions.

Cette information pourrait ensuite être entièrement récupérée (bien que sous forme chaotique) grâce au rayonnement libéré lors de son évaporation quantique – un processus initialement prédit par le même Hawking quarante ans auparavant.

L’idée n’est pas nouvelle : elle fait appel à un modèle d’univers holographique précédemment étudié par des centaines de physiciens, et objet d’un tel engouement qu’il a conduit certains d’entre eux à imaginer des scénarios parfaitement surréalistes. Par exemple, S. Mathur a proposé qu’au lieu d’être détruit par des forces de marée gravitationnelles ou par un pare-feu quantique, un astronaute tombant dans un trou noir serait simplement converti en hologramme, sans se rendre compte de rien [2].

A l’annonce de Hawking la communauté scientifique a donc dans son ensemble réagi avec beaucoup de prudence et de scepticisme, pour ne pas dire d’embarras devant l’annonce prématurée d’une idée non élaborée sur le plan technique : comment l’information s’inscrit-elle dans l’horizon des événements, comment est-elle restituée au monde extérieur, aucun détail n’a encore été donné.[3]

Pour y voir plus clair, un retour en arrière sur la thermodynamique des trous noirs s’impose.

Thermodynamique des trous noirs et paradoxe de l’information

Au cours des années 1970 – âge d’or de la théorie des trous noirs en relativité générale classique -, il a été démontré d’une part que l’état final d’un trou noir à l’équilibre ne dépendait que de trois paramètres : sa masse M, son moment angulaire J et sa charge électrique Q, ce qui paradoxalement faisait de lui l’objet le plus simple de toute la physique ; d’autre part, que la dynamique des trous noirs en interaction se résumait en quatre lois présentant une analogie extrêmement frappante avec celles de la thermodynamique usuelle[4]. En particulier, la seconde loi stipule que l’aire d’un trou noir ne peut jamais décroître au cours du temps. Ce résultat fondamental suggère une connexion étroite entre l’aire d’un trou noir et l’entropie d’un système thermodynamique. Continuer la lecture →

Actualités, Astronomie, Sciences

Evénements ondes gravitationnelles : un résumé en images

9 commentaires

Les événements GW150914 et GW151226

Résumé en 5 images extraites d’une de mes présentations powerpoint sur les trous noirs
DiapoGW1
Le mystère des ondes gravitationnelles, posé il y a un siècle par Albert Einstein dans un article paru en mars 1916, met en jeu les infimes variations de courbure de l’espace-temps engendrées par le mouvement d’objets relativistes. En haut à gauche : vue d’artiste figurant les ondes gravitationnelles engendrées par un système binaires d’étoiles compactes (étoiles à neutrons et/ou trous noirs). En haut à droite : vue d’artiste des ondes gravitationnelles engendrées par l’effondrement (non sphérique) d’une étoile en trou noir. En bas au centre : rappel du fait que l’existence des ondes gravitationnelles a d’abord été prouvée indirectement en 1974 grâce à l’analyse d’un pulsar binaire (couple d’étoiles à neutrons), dont la période orbitale décroît à la suite de la perte d’énergie due aux ondes gravitationnelles.

 

DiapoGW2
Les premières détections directes des ondes gravitationnelles ont été effectuées le 14 septembre 2015 (événement GW150914) et le 26 décembre 2015 (événement GW151226) par les deux détecteurs du programme LIGO situés aux Etats-Unis. Séparés par 3000 km, les détecteurs reçoivent le même signal à un centième de seconde d’intervalle, puisque les ondes gravitationnelles se déplacent à la vitesse de la lumière dans le vide, 300 000 km/s.

 

DiapoGW3
La comparaison entre le calcul théorique (en haut) et les données reçues (en bas) montre sans ambiguïté que le signal gravitationnel provient de la fusion de deux trous noirs en un trou noir unique, en trois phases extrêmement brèves (le tout durant moins d’une seconde dans la bande de fréquence dans laquelle les détecteurs sont sensibles): phase d’approche des deux trous noirs, fusion (signal maximum), vibration et stabilisation du trou noir final.

 

La modélisation des événements GW150914 et GW152612 permet notamment de déduire les masses des trous noirs mis en jeu. Il s’agit en l’occurrence de trous noirs “stellaires”, bien que dans l’événement du 14 septembre 2015 les masses sont sensiblement plus élevées que la “normale”, ce qui soulève d’intéressantes questions sur la formation de tels couples. La masse du trou noir final est, dans les deux cas, inférieure à la somme des masses des trous noirs parents : en vertu de la formule E=mc2, la différence a précisément été évacuée sous forme d’énergie gravitationnelle propagée par les ondes. Dans les deux cas aussi, ces événements se sont produits il y a près de 1,5 milliards d’années dans le passé. Notons qu’un troisième événement similaire, semblant lui aussi émaner d’une fusion de trous noirs situés cette fois à plus de 3 milliards d’années-lumière, a été observé le 12 octobre 2015, mais sa signification statistique n’est pas suffisante pour le qualifier. Cela implique d’une part que les couples de trous noirs sont beaucoup plus nombreux que ce que prédisaient les modèles conventionnels, d’autre part que ces détections pourraient être faites à un rythme de quelques dizaines par an, bien plus grand que prévu.

 

DiapoGW5

Et pour approfondir le sujet des ondes gravitationnelles, voir ma suite de 4 billets de février dernier consacrés au sujet :

https://blogs.futura-sciences.com/luminet/2016/02/10/la-lumiere-gravitationnelle-1/

https://blogs.futura-sciences.com/luminet/2016/02/10/la-lumiere-gravitationnelle-22/

https://blogs.futura-sciences.com/luminet/2016/02/13/la-lumiere-gravitationnelle-34-levenement-gw150914/

https://blogs.futura-sciences.com/luminet/2016/02/20/la-lumiere-gravitationnelle-44-le-futur-est-dans-lespace/

Actualités, Astronomie, Histoire des sciences

Les passages de Mercure (2/2) : de Halley à aujourd’hui

Un commentaire

Suite du billet précédent Les passages de Mercure (1/2) : de Kepler à Gassendi et fin

Après la première observation du transit de Mercure du 7 novembre 1631 par Pierre Gassendi, les passages suivants vont susciter un intérêt astronomique de plus en plus grand. Celui du 9 novembre 1644 est toutefois invisible en Europe. Idem pour celui du 3 novembre 1651, mais il est observé par Jeremy Shakerley à Surat (Inde). Le passage du 3 mai 1661 est observé par le célèbre Hevelius à Dantzig (Gdansk), en Pologne. Celui du 4 novembre 1664 n’est pas documenté, et celui du 7 novembre 1674 est invisible en Europe.

N’arrêtez pas votre lecture à cette fastidieuse énumération : le cours de l’histoire de l’astronomie va changer avec le transit de Mercure du 7 novembre 1677 ! Voici pourquoi.

La distance Terre-Soleil par la méthode des transits

La troisième loi du mouvement planétaire formulée par Kepler en 1618, qui donne une relation entre la période de révolution d’une planète et le demi-grand axe de son orbite, permet de connaître la taille du système solaire à un facteur d’échelle près. La connaissance d’une seule distance entre planètes ou entre une planète et le Soleil suffit donc pour calculer toutes les autres.

La parallaxe solaire est l’angle sous lequel on voit le rayon de la Terre depuis le Soleil. La connaissance de la parallaxe est donc équivalente à la connaissance de la distance Terre-Soleil.

parallaxe-solaireLe problème pratique est que l’angle est si petit qu’il est extrêmement difficile à mesurer (on sait aujourd’hui qu’il est égal à 8,794 secondes d’arc, soit 1/200 le diamètre apparent de la Lune). Les mesures et calculs effectués depuis l’Antiquité surestimaient considérablement cet angle, donc sous-estimaient la valeur réelle de la distance Terre-Soleil.

Cette pièce de 50 pence célèbre le voyage de Halley à Sainte-Hélène en 1576 et montre le passage d'une comète qui le rendra mondialement célèbre.
Cette pièce de 50 pence célèbre le voyage de Halley à Sainte-Hélène en 1676 et montre le passage de la comète de 1682 à qui il donnera son nom et qui le rendra mondialement célèbre.

Or, en 1677, sur l’île de Sainte-Hélène où il s’est rendu pour établir un catalogue des étoiles du ciel austral, le grand astronome anglais Edmund Halley (1656-1742) observe le passage de Mercure qui a lieu le 7 novembre. Il bénéficie d’un beau temps inespéré, et d’une durée de transit de  5h 14m. De retour en Angleterre, Halley  imagine une méthode simple mais géniale pour déterminer la parallaxe solaire. Sa méthode est basée sur la comparaison des temps de transit de Mercure ou de Vénus, mesurés depuis plusieurs lieux terrestres situés à des latitudes différentes. La différence des temps de passages observés donne accès à la parallaxe du Soleil. On remplace ainsi une difficile mesure de très petit angle par des mesures de temps. Continuer la lecture →

Actualités, Astronomie, Histoire des sciences

Les passages de Mercure (1/2) : De Kepler à Gassendi

5 commentaires

Le 9 mai, la planète Mercure va traverser le disque solaire d’est en ouest en environ sept heures et demi, et sera visible sous forme d’une minuscule tache noire – un phénomène astronomique appelé transit. Il va de soi que, pour qu’une planète transite sur le disque solaire, elle doit passer entre la Terre et le Soleil. Seules Mercure et Vénus peuvent donc être observées de la Terre lors de leur transit. Il y a en moyenne 13 passages de Mercure et deux passages de Vénus par siècle.

Mercure apparaît tout en bas du disque solaire sur cette image du transit du 7 mai 2003 (à ne pas confondre donc avec la tache solaire proche du centre, de taille apparente beaucoup plus grande).
Mercure apparaît tout en bas du disque solaire sur cette image du transit du 7 mai 2003 (à ne pas confondre donc avec la tache solaire proche du centre, de taille apparente beaucoup plus grande).

Tous les passages de Mercure se produisent aux mois de mai et novembre, aux alentours respectivement du 7 et du 9 du mois, le phénomène se répétant à des intervalles de 13 ou 33 ans en mai, ou tous les 7, 13 ou 33 ans en novembre. C’est donc une observation relativement rare, ce qui explique son intérêt pour les astronomes. Le transit de Mercure du 9 mai 2016 sera le premier depuis le précédent, en novembre 2006, et avant le prochain qui aura lieu en novembre 2019.

Comme le montre la carte de visibilité ci-dessous, il sera observable (moyennant un ciel dégagé !) depuis l’Europe, l’Afrique, les Amériques et une partie de l’Asie.

Transit Mercure 2016

Nombre d’excellents blogs, comme ceux de Futura Sciences ou celui de Guillaume Cannat intitulé Autour du Ciel, consacreront ou ont déjà consacré des billets détaillés à cet événement astronomique pas si fréquent. Mon présent billet ne sera donc pas consacré à l’actualité du transit mercurien, mais à sa très intéressante histoire.

De Kepler à Gassendi

La prévision des passages de Mercure et de Vénus devant le Soleil nécessite une bonne connaissance des mouvements orbitaux des planètes intérieures. Les tables dont disposaient les astronomes au début du XVIIe siècle n’étaient que peu fiables, qu’il s’agisse des classiques Tables Alphonsines fondées sur le système de Ptolémée, ou des plus récentes Tables Pruténiques fondées sur le système de Copernic. Lorsque Gaultier de la Valette (1564 – 1617), vicaire général d’Aix et excellent astronome amateur qui, en 24 novembre 1610 et en compagnie de Nicolas Fabri de Peiresc avait été le premier en France à observer à la lunette les quatre satellites de Jupiter, essaye de calculer le moment d’une conjonction du Soleil avec Mercure en mai 1631, il se retrouve presque au désespoir. Le 12 avril 1631 il écrit à Peiresc « L’on ne peut deviner quelles tables seront plus véritables. Je ne manquerai pourtant, durant ces trois ou quatre jours, faire tout mon possible si nous pouvons voir cette belle observation, qui nous découvrirait de belles choses en la nature, nous assurerait du mouvement de ladite planète, de sa distance au soleil, de la grandeur de son orbe, de sa révolution et de son cours suivant l’opinion de Copernic, et nous faisait encore voir de quelles tables les Astronomes ou Astrologues se doivent plus assurément servir : des Pruténiques, Daviques, Rudolphines ou Alphonsines ». Continuer la lecture →

Actualités, Astronomie, Sciences

Les comètes de Pâques : Hyakutake, la grande comète de l’an 1996

Laisser un commentaire

Les début de printemps et les fêtes pascales semblent décidément propices aux apparitions de comètes. L’étoile mouvante qui accompagna les Rois Mages vers la crèche de Jésus – dont nombre d’études historiques suggèrent la naissance non pas à Noël mais bien à Pâques – était-elle une comète ? Vraisemblablement, tout au moins si pareil événement s’est réellement produit.

Dans cette célèbre fresque de l'Adoration des Mages, réalisée par Giotto en 1303, l'étoile de la Nativité est représentée sous forme d'un astre chevelu, autrement dit une comète. Nombre d'historiens estiment qu'il s'agit probablement d'une fidèle reproduction de la brillante comète vue en 1301 dans les cieux d'Europe, comète qui sera plus tard identifiée comme étant la comète périodique de Halley.
Dans cette célèbre fresque de l’Adoration des Mages, réalisée par Giotto en 1303, l’étoile de la Nativité est représentée sous forme d’un astre chevelu, autrement dit une comète. Nombre d’historiens estiment qu’il s’agit probablement d’une fidèle reproduction de la brillante comète vue en 1301 dans les cieux d’Europe, comète qui sera plus tard identifiée comme étant la comète périodique de Halley.

Cette année 2016, ce sont deux petites sœurs jumelles aux  noms charmants de P/2016 BA14 et 252P/Linear qui, après être passées à quelques millions de kilomètres de la Terre lundi 21 et mardi 22 mars, ont augmenté en luminosité et sont devenues visibles dans l’hémisphère nord de la Terre en ce vendredi pascal, 25 mars 2016. Je n’en dirai pas plus, le sujet ayant été abondamment traité dans la blogosphère astronomique, notamment sur le site de Futurasciences et l’excellent blog Autour du ciel tenu par Guillaume Cannat.

Ce billet a en réalité pour but de vous ramener vingt années en arrière, en compagnie de l’une des plus brillantes comètes de Pâques jamais vues de mémoire d’homme. Cette année-là donc,  le 30 janvier 1996, un astronome amateur japonais, Yuji Hyakutake, eut la chance de découvrir une nouvelle comète qui allait désormais porter son nom. D’après les calculs, la comète atteindrait au moins la magnitude 1, soit celle des étoiles les plus brillantes du ciel, et serait visible à l’œil nu pendant tout le mois d’Avril, voyageant  de la constellation de la Grande Ourse en direction de celle  du Taureau. Hyakutake respecterait-elle  ses promesses ? Elle serait alors l’une des plus belles comètes de cette fin de XXe siècle, en attendant la très prometteuse Hale-Bopp annoncée pour le début 1997. Continuer la lecture →

Actualités, Astronomie, Sciences

La “lumière gravitationnelle” (4/4) : le futur est dans l’espace

12 commentaires

Suite du billet précédent : L’événement GW150914

Pour détecter des ondes gravitationnelles de moindre amplitude ou de plus basse fréquence que celles accessibles à la génération d’interféromètres au sol comme LIGO et VIRGO, il faudra envoyer les détecteurs dans l’espace. C’est tout l’enjeu du projet phare de l’ESA baptisé eLISA (bel acronyme signifiant en anglais european laser interferometric space antenna, soit « antenne spatiale interférométrique à laser »). Il s’agit d’expédier trois satellites en orbite autour du Soleil, disposés chacun aux sommets d’un triangle équilatéral de 5 millions de kilomètres de côté et reliés par des faisceaux laser. Sur une aussi grande longueur, le passage d’une onde gravitationnelle de basse fréquence devrait engendrer une fluctuation significative de la distance entre les satellites, mesurable par les lasers embarqués. Reste bien sûr à stabiliser les distances entre les satellites avec une précision jamais atteinte, ce qui suppose de compenser par exemple la pression du vent solaire et autres influences parasites. C’est pour tester cet élément décisif que l’Agence Spatiale Européeenne a lancé fin 2015 la sonde “d’éclairage” LISAPathfinder, qui en janvier 2016 est parvenue au point de Lagrange L1, à 1,5 millions de km de la Terre et a libéré deux masses-étalon séparées seulement de 38 cm.  Il s’agit de s’assurer qu’en l’absence d’onde gravitationnelle, cette distance ne varie pas de plus d’un millionième de l’épaisseur d’un cheveu humain, auquel cas le passage d’une onde gravitaitonnelle serait détectable.   Si tout fonctionne, l’interféromètre complet eLISA pourrait être placé en orbite en … 2034. Un peu de patience est donc requise…

Le schéma de principe de l’observatoire eLISA consiste en trois satellites en formation équilatérale, séparés chacun de 5 millions de kilomètres, l’ensemble tournant autour du Soleil.

Le schéma de principe de l’observatoire eLISA consiste en trois satellites en formation équilatérale, séparés chacun de 5 millions de kilomètres, l’ensemble tournant autour du Soleil.

eLISA et les interféromètres au sol LIGO et VIRGO seront complémentaires ; leurs domaines de fréquences n’étant pas les mêmes, les sources observables seront différentes. Affranchi des ondes sismiques, eLISA travaillera dans les basses fréquences, comprises entre 0,0001 et 1 hertz – domaine intéressant pour capter les trous noirs massifs.

Les instruments au sol VIRGO et LIGO ne seront pas rendus obsolètes par l’interféromètre spatial LISA, car leurs domaines de fréquences et de sensibilité seront différents. VIRGO et LIGO détecteront les effondrements de supernovae en trous noirs, et les coalescences d’étoiles à neutrons et de trous noirs stellaires. LISA fonctionnera dans la gamme des sources X binaires situées dans notre galaxie, et celle des couples de trous noirs géants dans les galaxies lointaines.
Les instruments au sol VIRGO et LIGO ne seront pas rendus obsolètes par l’interféromètre spatial LISA, car leurs domaines de fréquences et de sensibilité seront différents. VIRGO et LIGO détecteront les effondrements de supernovae en trous noirs, et les coalescences d’étoiles à neutrons et de trous noirs stellaires. LISA fonctionnera dans la gamme des sources X binaires situées dans notre galaxie, et celle des couples de trous noirs géants dans les galaxies lointaines.

L’observation d’une coalescence de trous noirs massifs par eLISA sera spectaculaire. Pour un couple de trous noirs de 1 million de masses solaires chacun, eLISA surveillera les 40 derniers jours de leur phase spiralante, soit 600 orbites, et l’amplitude du signal atteindra 10–17 à la distance fabuleuse de 3 milliards d’années-lumière. Environ 10 000 fois supérieur au bruit, cet intense signal fournira une localisation extraordinairement précise d’un événement, et l’identification optique de l’amas de galaxies où il sera produit déterminera avec une précision du pour cent les paramètres clés des modèles cosmologiques, comme le taux d’expansion de l’Univers et sa densité d’énergie moyenne. On pourra alors confirmer ou non si notre Univers est essentiellement rempli d’une forme d’« énergie noire », dont l’effet accélérateur sur l’expansion cosmique modifierait le destin de l’Univers tout entier.

Malgré l’observation de quelques galaxies géantes à double noyau actif associées vraisemblablement à des couples de trous noirs géants, le phénomène de fusion de tels trous noirs massifs se produit rarement. En revanche, tapi au cœur d’une galaxie, un trou noir massif célibataire capture plus souvent des étoiles. Nous avons vu au chapitre précédent que, lorsqu’elles sont de type solaire, c’est-à-dire peu denses, les étoiles sont détruites par les forces de marée en s’approchant du trou noir. Cependant, les astres compacts comme les étoiles à neutrons et les trous noirs de masse stellaire perdurent sans être brisés et chutent en spiralant jusqu’à l’horizon du trou noir. eLISA détectera les ondes gravitationnelles émises par ce phénomène et assistera à la dernière année de la vie d’une étoile compacte chutant en spirale dans un trou noir de 1 million de masses solaires, et ce jusqu’à une distance de plusieurs centaines de millions d’années-lumière.

La galaxie active Markarian 315 possède un noyau double, résultant de la fusion de deux galaxies. Chaque noyau abrite vraisemblablement un trou noir massif, en orbite l’un autour de l’autre. Actuellement distants de 6 000 années-lumière, ils finiront par fusionner et par produire une bouffée d’ondes gravitationnelles de forte amplitude mais de basse fréquence, détectable par un interféromètre spatial.
La galaxie active Markarian 315 possède un noyau double, résultant de la fusion de deux galaxies. Chaque noyau abrite vraisemblablement un trou noir massif, en orbite l’un autour de l’autre. Actuellement distants de 6 000 années-lumière, ils finiront par fusionner et par produire une bouffée d’ondes gravitationnelles de forte amplitude mais de basse fréquence, détectable par un interféromètre spatial.

L’enregistrement du signal gravitationnel durant cette année de chute permettra de cartographier la structure de l’espace-temps autour du trou noir massif. On comparera alors cette structure observée à la solution mathématique de Kerr qui décrit les trous noirs en rotation. Cette solution prédit une forme de la courbure de l’espace-temps spécifique aux trous noirs : ni étoile ni amas d’étoiles ne peuvent courber l’espace-temps de cette manière. On pourra alors conclure définitivement à l’existence des trous noirs dans l’Univers.

L’histoire récente de l’astronomie a prouvé que, chaque fois que l’homme a scruté le ciel par d’autres yeux que les siens, de nouvelles merveilles lui sont apparues, le forçant à réviser ses conceptions et améliorant un peu plus sa compréhension de l’Univers.

Avec la détection de l’événement GW150914 en septembre 2015, la fenêtre gravitationnelle vient juste d’être ouverte. Maintenant que les premiers signaux directs sont captés, l’information sur le mouvement et la nature des sources reste encore noyée dans beaucoup de bruit parasite. Mais, animés de la certitude que l’astronomie gravitationnelle est celle des siècles futurs, nous lancerons bientôt dans l’espace de gigantesques interféromètres parfaitement isolés des secousses telluriques et de l’agitation humaine…