Suite du billet précédent (2) : L’apport de Galilée
Peiresc, le prince des curieux
Nicolas-Claude Fabri de Peiresc naît le 1er décembre 1580 à Belgentier, petite commune de Provence située entre Aix et Toulon. Sa vie nous est essentiellement connue par la biographie qu’en fit son grand ami Pierre Gassendi[i].

Adolescent, Peiresc est élève des jésuites dans leurs collèges d’Avignon puis de Tournon ; à l’âge de seize ans il y reçoit un enseignement d’astronomie, qui le passionne malgré l’austérité de cette science qui à l’époque se limite à inventorier les étoiles et, par des mesures d’angles à l’arbalestrille ou à l’astrolabe, à suivre leurs mouvements. Peiresc revient ensuite faire sa philosophie à Aix-en-Provence, puis se rend à Padoue pour étudier le droit, tout en suivant nombre d’autres enseignements.

Il se lie rapidement avec l’humaniste italien Gian Vincenzo Pinelli (1535-1601), qui devient son maître et modèle. C’est de Pinelli, dont la bibliothèque aurait été la plus vaste du XVIe siècle, que Peiresc tirera son goût immodéré pour les livres et les cabinets de curiosité. C’est chez lui également qu’il rencontre pour la première fois Galilée, à qui Pinelli avait ouvert sa bibliothèque.
Après plus de trois ans passés en Italie et à la mort de Pinelli qui l’affecte profondément, Peiresc revient en France pour continuer ses études de droit. Il séjourne à Montpellier pour passer sa thèse de doctorat puis, après divers voyages à Paris, Londres et les Flandres, il est nommé conseiller au Parlement de Provence. L’astronomie va cependant rester l’une de ses occupations majeures : jamais il ne s’éloignera de cette discipline et, par périodes, lui consacrera toute son activité.

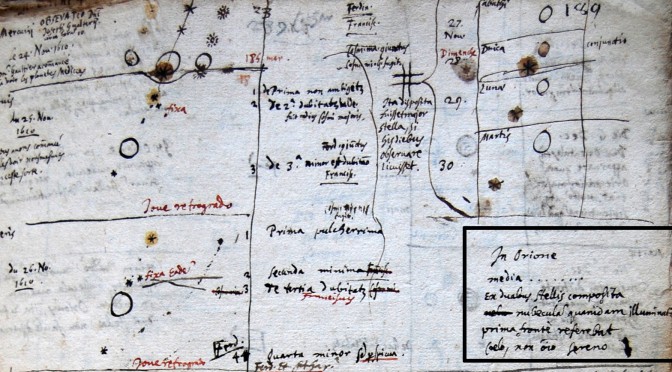
Dès l’automne 1604, Peiresc observe la rencontre des trois planètes supérieures Mars, Jupiter et Saturne, événement qui ne se produit que tous les huit cents ans et qu’on appelle la Grande Conjonction. En même temps paraît une étoile de la grandeur de Jupiter, qu’on voit plus d’un an à l’un des pieds de la constellation du Serpentaire. Peiresc n’ayant pas encore de globe céleste pour s’assurer du nombre des étoiles fixes, croit qu’il s’agit d’une étoile déjà répertoriée par les Anciens. Cependant, par les lettres qu’il reçoit quelques mois après, il apprend qu’il s’agit d’une nouvelle étoile, que Galilée observe en même temps que lui et dont l’apparition porte un coup de plus à la doctrine aristotélicienne de l’immuabilité du ciel des fixes. Ces « étoiles nouvelles » sont appelées de nos jours des supernovæ. Celle observée par Peiresc est connue sous le nom de « supernova de Kepler », car ce dernier l’observa pendant près d’un an et en tira d’intéressantes leçons.[ii] Continuer la lecture de La révolution copernicienne chez les humanistes provençaux (3) : Peiresc