Archives pour l'étiquette entropie

Astronomie, Mes publications, Sciences

L’univers holographique (3) : De l’entropie à l’hypothèse holographique

5 commentaires

Suite du billet précédent L’univers holographique (2) : la gravité quantique façon théorie des cordes

Dans le cadre de la théorie des cordes, il s’agissait dans un premier temps de retrouver les lois de la thermodynamique classique des trous noirs, c’est-à-dire savoir calculer, en termes de mécanique statistique quantique, leur entropie et leur température en fonction de leur aire et de leur gravité de surface. La tâche n’est pas aisée. Comme en thermodynamique, l’entropie mesure le nombre total d’états microscopiques internes correspondant à un état externe donné du trou noir, défini par ses trois paramètres (M, J, Q). Encore faut-il comptabiliser les « vrais » états microscopiques, c’est-à-dire les degrés de liberté ultimes sur lesquels il faut calculer l’entropie. Pour évaluer le contenu ultime en informations d’un élément de matière, c’est-à-dire son entropie thermodynamique, il faut en toute rigueur connaître ses constituants fondamentaux au niveau le plus profond de structuration. Dans le modèle standard de la physique des particules, les quarks et les leptons semblent suffisants pour coder toute l’information. Mais dans la théorie des cordes et sa théorie-mère (M-theory), les quarks et les leptons sont des états excités de supercordes, qui deviennent alors les constituants les plus élémentaires du monde physique.

Gerard 't Hooft, né en 1946 aux Pays-Bas, est professeur à l'Institut de physique théorique de l'université d'Utrecht depuis 1977.
Gerard ‘t Hooft, né en 1946 aux Pays-Bas, est professeur à l’Institut de physique théorique de l’université d’Utrecht depuis 1977.

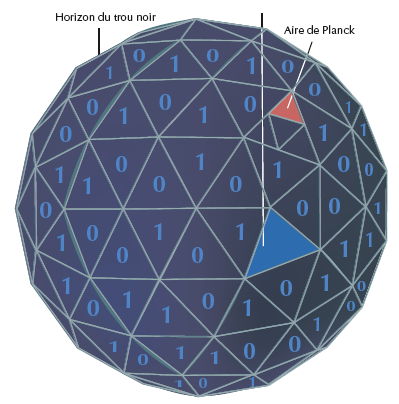
En 1993, Gerard t’Hooft (futur lauréat du prix de Nobel de physique 1999 pour ses travaux sur l’interaction électrofaible)  fut le premier à revisiter le travail de Hawking sur la thermodynamique des trous noirs dans le cadre de la théorie des cordes. Il calcula que le nombre total de degrés de liberté dans le volume d’espace-temps intérieur au trou noir était proportionnel à la superficie de son horizon[1]. La surface bidimensionnelle du trou noir peut être divisée en unités quantiques fondamentales appelées aires de Planck (10–66 cm2). Du point de vue de l’information, chaque bit sous forme de 0 ou de 1 correspond à quatre aires de Planck, ce qui permet de retrouver la formule de Bekenstein-Hawking S = A/4 pour l’entropie. Tout se passe comme si l’information perdue pour un observateur extérieur – l’entropie du trou noir – portée initialement par la structure 3D des objets ayant traversé l’horizon des événements, était codée sur sa surface 2D à la façon d’un hologramme, et t’Hooft en conclut que l’information avalée par un trou noir devait être intégralement restituée lors du processus d’évaporation quantique.

L’entropie d’un trou noir est proportionnelle à la surface de son horizon. Un trou noir dont l’horizon est constitué de A aires de Planck a une entropie de A/4 unités. Une aire de Planck (10–66 cm2) est l’unité quantique fondamentale de surface. Du point de vue de l’information, tout se passe comme si l’entropie était inscrite sur l’horizon du trou noir et que chaque bit d’information, sous forme de 0 ou de 1, correspondait à quatre aires de Planck.
L’entropie d’un trou noir est proportionnelle à la surface de son horizon. Un trou noir dont l’horizon est constitué de A aires de Planck a une entropie de A/4 unités. Une aire de Planck  est l’unité quantique fondamentale de surface. Du point de vue de l’information, tout se passe comme si l’entropie était inscrite sur l’horizon du trou noir et que chaque bit d’information, sous forme de 0 ou de 1, correspondait à quatre aires de Planck.

Continuer la lecture →

Arts, Musique

Du piano aux étoiles (3/3)

18 commentaires

Ceci est la suite du billet précédent

Si je devais avoir un seul regret dans ma vie de mélomane par ailleurs bien remplie, c’est d’être toujours resté à des années-lumière du niveau pianistique qui m’aurait permis de jouer les grandes pièces du répertoire, comme la Sonate en si mineur de Liszt (ici par l’immense Nelson Freire), les Etudes de Chopin (Alfred Cortot, bien sûr) ou les Préludes de Rachmaninov (Sviatoslav Richter s’impose). Mais il m’arrive parfois de faire d’extraordinaires rêves musicaux, dans lesquels toutes les irritantes contraintes du réel sont bannies…

En récital à la Halle Saint-Pierre le 15 mai 2011, croqué sur le vif par mon ami Jean Letourneur
En récital à la Halle Saint-Pierre le 15 mai 2011, croqué sur le vif par mon ami Jean Letourneur

 Quitte à passer pour une vieille barbe rétrograde, j’avoue rester totalement hermétique à ce que depuis quatre décennies les peuples de notre planète toute entière, les marchands, les médias, les clients et les soi-disant élites intellectuelles et politiques entendent par musique : à savoir une forme de divertissement chanté, dansé ou les deux, sur une base rythmique binaire à peu près fixe et trois accords élémentaires. Pour moi la musique, qu’il s’agisse de classique, de jazz ou de la plupart des musiques traditionnelles, c’est l’exact opposé : du noble, du complexe, du transcendant.  Je considère en fait que la complexité structurelle a une véritable valeur esthétique. Un de mes collègues mathématicien et musicien de l’Université Libre de Bruxelles, J.-P. Boon, a récemment publié une étude  montrant que l’on peut mesurer la complexité d’une pièce musicale en termes d’entropie. L’entropie dite de Shannon est une fonction mathématique qui correspond à la quantité d’information contenue ou délivrée par une source quelconque d’information. Quand l’entropie d’un système est basse, le système contient beaucoup d’informations, quand l’entropie augmente, l’information se dégrade. L’entropie de Shannon est calculable pour toute collection d’octets, qu’il s’agisse d’un fichier informatique, d’un texte littéraire, d’une œuvre picturale ou d’une pièce musicale. En effet, la seconde loi de la thermodynamique est universelle, elle s’applique aussi bien aux systèmes physiques qu’au comportement humain et à ses représentations artistiques.

Continuer la lecture →