huile sur panneau de bois, 48 × 34 cm. Musée du Louvre, Paris
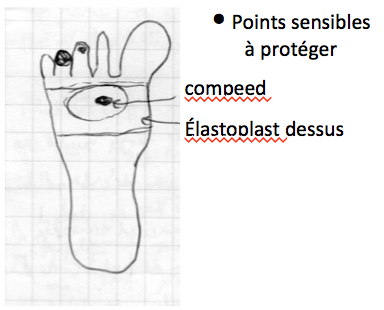
Lucas van Leyden, ou Lucas de Leyde (vers 1494–1533), est l’un des plus grands peintres et graveurs néerlandais de la Renaissance. Connu pour ses scènes religieuses, mythologiques et profanes, il se distingue par une grande finesse de dessin, une attention aux détails narratifs, un intérêt marqué pour les paysages et les arrière-plans. Il a été l’un des premiers artistes des Pays-Bas à intégrer des éléments humanistes et à montrer une influence italienne dans son travail.
Son tableau Loth et ses filles[1], daté de la période 1520-1525, traite de l’épisode biblique (Genèse 19) où lequel Dieu décide de détruire les villes corrompues de Sodome et Gomorrhe. Loth, neveu vertueux d’Abraham, est prévenu par des anges qui lui enjoignent de fuir la ville avec son épouse et ses deux filles, avec toutefois l’interdiction de se retourner. La femme, curieuse et désobéissant à l’interdiction, est changée en statue de sel. Loth se réfugie finalement dans une grotte avec ses deux filles. Pensant que l’humanité est anéantie, ces dernières enivrent leur père pour s’unir à lui et assurer une descendance.
Le thème a fasciné de nombreux peintres de la Renaissance, comme Peter Paul Rubens (1614), Guido Reni (1615), Orazio Gentileschi (vers 1620) et sa fille Artemisia (1638) ou encore Simon Vouet (1633). Dans leurs toiles, Loth et ses filles occupent toute la scène, représentés de façon intime et ambiguë pour souligner l’érotisme et la transgression incestueuse, tandis que des jarres de vin rappellent l’ivresse du vieillard. Ce n’est que dans les chefs-d’œuvre de Lucas van Leyden (vers 1520) et de Lucas Cranach l’Ancien (vers 1528) que l’on a en arrière-scène un aperçu spectaculaire de la destruction de Sodome : feu tombant du ciel, flammes et colonnes de fumée montrant la ville en train de brûler et les navires couler.

56 cm x 37 cm. Kunsthistorisches Museum, Vienne (Autriche)
Les personnages sont certes placés au premier plan, isolés, dans une intimité troublante, mais à l’arrière-plan, on distingue les flammes de Sodome, ainsi qu’un paysage vallonné, typique de l’art flamand et hollandais.
La peinture mêle un réalisme minutieux dans les visages, les vêtements, les éléments naturels. Les attitudes des personnages sont expressives mais mesurées, sans dramatisation excessive. Loth apparaît passif, presque inconscient, tandis que les filles affichent des gestes ambigus, entre tendresse et séduction.
La destruction de Sodome est représentée de manière spectaculaire à l’arrière-plan droit. Le ciel est zébré de flammes et de traînées lumineuses, symbolisant la colère divine. La ville est en proie aux flammes, avec des bâtiments en ruine et des navires engloutis dans le port, accentuant le chaos et la désolation. Cette scène apocalyptique contraste fortement avec le calme apparent du premier plan.
Un détail poignant, que l’on trouve également dans la toile de Cranach, est la représentation de la femme de Loth, transformée en statue de sel pour avoir désobéi à l’interdiction de se retourner. Elle est visible sur un pont en bois, figée, tandis que Loth et ses filles poursuivent leur fuite, accompagnés d’un âne.

La composition est divisée verticalement par un arbre élancé, séparant le drame céleste de la scène terrestre. Au premier plan gauche, devant une tente rouge, Loth est assis, embrassant l’une de ses filles, tandis que l’autre verse du vin dans une coupe, préparant l’ivresse de leur père.
Cette peinture est un exemple remarquable du maniérisme hollandais, mêlant drame biblique, symbolisme moral et maîtrise technique. Elle offre une vision saisissante de la colère divine et des punitions humaines qui en découlent. Continuer la lecture de Colère divine ou chute météoritique ?