Début d’une série de billets adaptés d’un article paru en anglais dans la revue Inference
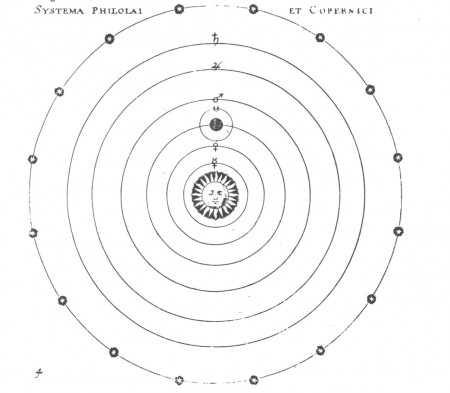
Le Soleil fixe au milieu des planètes
Dans le premier livre, je décris toutes les positions des orbes, ainsi que les mouvements que j’attribue à la Terre, afin que ce livre contienne pour ainsi dire la constitution générale de l’univers.
Nicolas Copernic, lettre-préface au pape Paul III, Des révolutions des orbes célestes, 1543 (trad. A. Koyré, Paris, Alcan, 1934)

L’œuvre princeps du chanoine polonais Nicolas Copernic (1473-1543), De Revolutionibus orbium cœlestium[i], publiée l’année même de sa mort, a été le fruit d’un long travail préparatoire présenté pour la première fois en 1515 sous forme réduite et manuscrite dans le Commentariolus[ii], diffusé uniquement auprès d’un cercle restreint d’intellectuels. Le traité astronomique complet de 1543 est considéré par les historiens modernes comme étant à l’origine de la vision moderne de l’univers. Il a pour objet d’attaquer, en vue de la remplacer, la thèse géocentrique consacrée par Aristote quelque deux mille ans plus tôt, et confortée par l’astronome alexandrin Claude Ptolémée dans son célèbre Almageste, prestigieux monument de science observationnelle et mathématique écrit dans les années 140 de notre ère, et qui depuis lors régnait sur l’astronomie occidentale et arabe.
Conscient des imperfections du système géocentrique de Ptolémée et soucieux de trouver une harmonie géométrique dans l’organisation du cosmos, Copernic réintroduit le système héliocentrique, modèle astronomique déjà évoqué dans l’Antiquité mais resté en sommeil, selon lequel le Soleil est au centre géométrique du monde tandis que la Terre tourne autour de lui en un an et sur elle-même en un jour. Ravalée au rang de simple planète, c’est-à-dire d’astre errant au même titre que Mercure, Vénus, Mars, Jupiter et Saturne, notre planète cesse ainsi d’occuper une position cosmologique privilégiée.
Dans la seconde moitié du XVIe siècle, le premier à mentionner le nom de Copernic en France est Omer Talon (1510-1562), un disciple de Petrus Ramus, dans les Academicae questiones de 1550 : la réception est plutôt favorable, car les ramistes sont hostiles à Aristote[iii]. En revanche, peu de ses contemporains prennent Copernic au sérieux, et les jugements sur l’héliocentrisme sont majoritairement négatifs. On lit notamment des railleries à l’égard de la thèse copernicienne chez les poètes de La Pléiade, comme le célèbre Du Bartas[iv] ou le moins connu Jean Bodin[v]. De fait, la doctrine de Copernic, jugée absurde car contraire à l’évidence sensorielle de l’immobilité terrestre, se répand très lentement ; le terme même de « révolution scientifique » qui lui est attaché n’a fait son apparition qu’au XXe siècle sous la plume de l’épistémologue Thomas Kuhn[vi].

Il se trouve entre nous des esprits frénétiques
Qui se perdent toujours par des sentiers obliques
Et, de monstres forgeurs, ne peuvent point ramer
Sur les paisibles flots d’une commune mer.
Tels sont comme je crois ces écrivains qui pensent
Que ce ne sont pas les cieux ou les astres qui dansent
A l’entour de la terre, mais que la terre fait
Chaque jour naturel un tour vraiment parfait.
Guillaume de Salluste du Bartas, La Sepmaine ou création du monde, 1578.
Cependant, Michel de Montaigne (1533-1592) fait figure d’exception en soutenant, dans ses Essais, non seulement la thèse héliocentrique, mais en percevant aussi l’œuvre de Copernic comme une révolution scientifique en train de s’accomplir. Pour en comprendre les raisons profondes, il faut rappeler la position fondamentalement sceptique de Montaigne concernant la philosophie de la connaissance.
Exercice de jugement sceptique sur l’astronomie
Montaigne reçoit une éducation humaniste dès son plus jeune âge ; il fait une carrière de magistrat, exerce la fonction de maire de Bordeaux et prend sa retraite à l’âge de trente-sept ans pour écrire et réviser, de 1571 à sa mort, les fameux Essais, qui sont des exercices de jugement. Continuer la lecture de La révolution copernicienne chez les humanistes provençaux (1) : Montaigne