Suite du billet précédent La physique étrange d’Interstellar (3/6)
En novembre 2014, le film de science-fiction Interstellar (réalisation Christopher Nolan, Warner Bros Pictures, 169 minutes, 2014) sortait sur nos écrans. Véritable « blockbuster » hollywoodien, il a suscité un énorme battage médiatique, comme en témoignent les innombrables forums de discussion et articles de presse ayant fleuri au cours des jours, semaines et mois qui ont suivi. A la demande de la revue de langue anglaise Inference : International Review of Science, j’ai par la suite fait un travail d’analyse scientifique beaucoup plus développé et approfondi, publié au printemps 2015. Je vous en livre la traduction française, découpée en 6 billets. Celui-ci est le quatrième.
Dilatation temporelle
La théorie de la relativité restreinte d’Einstein prédit que des observateurs placés dans des référentiels différemment accélérés perçoivent le temps différemment. Ce phénomène bien connu de « dilatation » temporelle a été vérifié expérimentalement à un haut degré de précision. Les conséquences de la dilation temporelle se font sentir tout au long de l’histoire d’Interstellar.
Près de l’horizon des événements d’un trou noir, où le champ gravitationnel est énorme, la dilatation temporelle est également énorme. Les horloges sont fortement ralenties par rapport aux horloges lointaines. Une heure sur Miller (temps propre de Miller) équivaut à sept années sur Terre. Ceci correspond à un facteur de dilatation de 60 000. Bien que la dilatation temporelle tende vers l’infini quand l’horloge tend vers l’horizon des événements, un facteur de dilatation de 60 000 est impossible pour une planète en orbite stable autour d’un trou noir.
Dans son livre, The Science of Interstellar, Kip Thorne explique qu’un facteur de dilatation temporelle de cette grandeur était une exigence non négociable de la part du réalisateur[1]. Après quelques heures de calcul, Thorne est parvenu à la conclusion que le scénario, bien que très peu vraisemblable, était marginalement possible. Le facteur-clé est la période de rotation du trou noir. Un trou noir de Kerr (tournant) se comporte très différemment d’un trou noir de Schwarzschild (statique). L’équation de dilatation temporelle dérivée de la métrique de Kerr s’écrit:
1 – (dτ/dt)2 = 2GMr/c2rho2, où rho2 = r2 + (J/Mc)2cos2θ.
En substituant dτ = 1 heure et dt = 7 ans, on obtient:
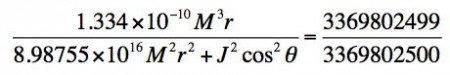Cette équation décrit un trou noir de masse M et de moment angulaire J, observé à la coordonnée radiale r et à la coordonnée angulaire θ. La fraction de droite transcrit l’effet de dilatation 1 heure = 7 ans. Dans la métrique de Schwarzschild, le rayon orbital ne peut être plus petit que trois rayons gravitationnels. Une dilatation temporelle de cette magnitude ne pourrait être obtenue pour la planète en question. Toutefois, la métrique de Kerr permet des orbites stables beaucoup plus proches de l’horizon. Les calculs indiquent que pour M = 108 masses solaires, r = 1.48 × 1013cm, θ = π, et J = 8.80275 × 1057J.s. Ceci implique que le trou noir doit posséder un moment angulaire très proche de la valeur maximale permise, et la planète une orbite circulaire couchée dans le plan équatorial de rayon pratiquement égal au rayon gravitationnel du trou noir.
Ceci est théoriquement possible, mais pas réaliste.
Le Processus de Penrose
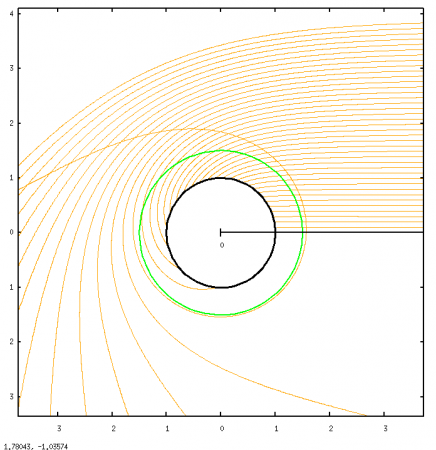
Bientôt à cours de carburant, avec une planète restant à explorer, le vaisseau Endurance exploite une forme particulièrement efficace d’assistance gravitationnelle afin de poursuivre sa mission. Décrit dans le film comme un effet de fronde, l’Endurance plonge dangereusement près de l’horizon des événements de Gargantua, avant d’en réchapper avec un gain d’énergie. Ce mécanisme, décrit correctement dans Interstellar, est connu sous le nom de processus de Penrose[2].
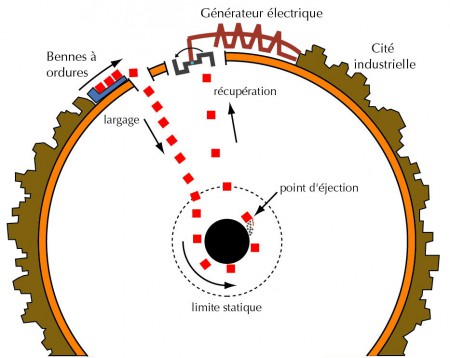
Les lois régissant la physique des trous noirs de Kerr nous disent que, bien que ni matière ni rayonnement ne puisse s’en échapper (dans la version non quantique de la relativité générale), un trou noir peut perdre une partie de son énergie rotationnelle. Le rôle-clé dans cette affaire est tenu par l’ergosphère, une région située entre une certaine distance extérieure à l’horizon appelée limite statique, et l’horizon lui-même, surface propre du trou noir. A l’intérieur de cette zone, l’espace-temps est lui-même irrésistiblement entraîné, comme dans un maelstrom marin, dans le sens de rotation du trou noir[3].
Dans une expérience de pensée remontant à 1969, Roger Penrose a calculé que si un projectile entrait dans l’ergosphère et se scindait en deux fragments, le premier, orbitant dans la direction contraire à la rotation du trou noir, tomberait dans l’horizon des événements, tandis que le second pourrait s’échapper en transportant une énergie plus grande que celle du projectile initial[4]. Remplaçons le projectile par un vaisseau spatial qui éjecte une partie de sa structure dans le trou noir le long d’une orbite rétrograde minutieusement calculée, et le tour est joué !
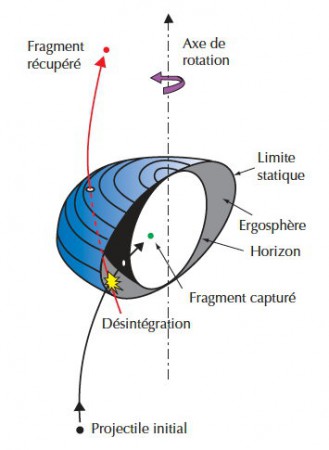
Les calculs indiquent qu’une énergie équivalente à la masse-énergie du fragment perdu dans le trou noir peut être récupérée, laquelle est déjà énorme en vertu de E = mc2. Mais une énergie additionnelle viendrait de la rotation du trou noir, freiné par le fragment capturé en sens contraire de sa rotation. Combien d’énergie rotationnelle pourrait-elle ainsi être exploitée ? Jusqu’à 29% de la masse du trou noir !
La suite est à lire ici : La physique étrange d’Interstellar (5/6): machines à remonter le temps et cinquième dimension
REFERENCES
[1] Kip Thorne, The Science of Interstellar (New York: W. W. Norton & Company, 2014), 154.
[2] Jean-Pierre Luminet, Le destin de l’univers, op. cit. chap. 14.
[3] Un phénomène de relativité générale appelé effet Lense–Thirring.
[4] Roger Penrose, “Gravitational Collapse: The Role of General Relativity,” Rivista del Nuovo Cimento, Numero Speziale 1 (1969): 252–76.
Bonjour Monsieur Luminet,
tout d’abord merci pour vos explications concernant ces phénomènes singuliers que sont les trous noirs.
N’étant pas compétent en ce domaine, mais soucieux de compléter ma compréhension du processus de Penrose , je souhaitais vous poser la question suivante:
y a-t-il, à votre connaissance, quelque résultat de cosmologie observationnelle corroborant ce processus (eg: même si, intuitivement, la probabilité qu’un tel événement semble ténue, un éventuel corps céleste suffisamment massif se scindant en deux au sein de l’Ergosphère du trou noir galactique?).
Cordialement,
Merci de me lire. Il existe une version astrophysique du processus de Penrose permettant d’extraire naturellement l’énergie de rotation d’un trou noir, non pas en désintégrant des particules, mais à l’aide des lignes du champ magnétique produit dans un dique d’accrétion. C’est le processus de Blandford-Znajek (proposé par ces derniers en 1977). Le processus est souvent invoqué pour expliquer l’émission de jets relativistes dans les radiogalaxies et les quasars.
Merci pour votre réponse.
Y a-t-il un lien possible entre l’émission de jets relativistes due au processus de Blandford-Znajek et l’existence spéculative de fontaines blanches?
Par ailleurs, il est souvent fait mention, dans les articles évoquant ce processus (eg: “A Unified Model for AGN” de Ryan Yamada, Astro 671, March 27, 2006), d’une masse de trou noir supermassif de 10E6 à 10E9 Masses Solaires (MS).
Quelle serait, de votre point de vue, et dans la mesure où cela fait sens, la conséquence d’une masse bien supérieure à 10E9 MS eu égard au processus de Blandford-Znajek?
Il n’y a en principe aucun lien entre les jets relativistes et les fontaines blanches, correspondant à des processus physiques complètement différents (même si tous deux liés à l’existence de trous noirs). Le processus de BZ requiert un champ magnétique gelé dans un vaste disque d’accrétion. Rien a priori n’empêche un trou noir hypermassif d’en posséder un. Toutefois, le trou noir le plus massif jusqu’ici détecté aurait une masse de 19 10E9 MS, mais il n’est pas garanti qu’il ait un disque d’accrétion (car il pourrait avoir avalé déjà tout le gaz disponible de la galaxie naine dans laquelle il se trouve).
Merci pour votre réponse.
Le phénomène de fontaine blanche serait-il donc l’effet hypothétique exclusif d’un transfert de matière à travers un trou de vers crée par le trou noir?
“perçoivent le temps différemment…”. Non. “Vivent” le temps differemment. Dire “percevoir” c’est continuer a penser en terme de temps universel. Or, si j’ai pigé quelque chose a Eintein, le temps universel ca n’existe pas: il n’y a que des temps locaux relatifs selon la vitesse relative de chaque localité par rapport a telle autre. En fait ce serait dire que chaque mouvement est la notion fondamentale qui fonde le temps, comme le posait le penseur dialectique oublié F.Engels (tabou de la doxa actuelle).
Vous avez raison, il s’agit bien ici de “vivre” différemment le temps, plutôt que simplement le “percevoir” (encore que l’on puisse percevoir que l’on vit…). Quant à Engels je ne pense pas qu’il soit oublié.
Bonjour,
Bravo et merci pour votre blog.
Je suis moins admiratif pour la partie commentaires (mais c’est le jeu ma pauvre Lucette). On a parfois l’impression de lire ceux de pro et anti Windows/ Apple. Le problème de l’homme c’est que souvent (toujours… peut-être) il cherche à avoir raison plutôt que trouver la vérité… quitte à avoir tord.
Et comme tout est question d’interprétation (n’est ce pas messieurs les religieux) je précise que mon attirance va plutôt vers les scientifiques. A condition toutes-fois qu’ils ne transforment pas la science en dogme.
Cordialement.
Merci. En effet il y a à boire et à manger dans les commentaires, mais c’est le jeu utile de l’échange. Il y a malgré tout un modérateur, et les “pires” commentaires (type fanatiques religieux, illuminés, etc.) ne sont pas publiés.
Bonjour, merci beaucoup pour cet article, il est très instructif. Je me demande si il n’existe pas une énorme incohérence dans le scénario : la planète de Miller suit une géodésique dans l’espace temps, donc elle est dans un référentiel inertiel. Ses horloges ne devraient pas être ralenties par le trou noir.
Pas d’incohérence sur ce point. La planète Miller a ses horloges qui ne sont pas “ralenties” dans leur temps propre. La distorsion temporelle par rapport au temps d’un observateur lointain ne se manifeste que pour l’astronaute qui va sur la planète puis en repart, en raison des variations extrêmes des champs de gravitation… Merci de m’avoir lu.
Bonsoir Monsieur Luminet,
Merci pour la vulgarisation exigeante de vos articles.
Une question me taraude longtemps après avoir vu le film Interstellar. La planète Miller est en orbite autour d’un trou noir hypermassif. Or, corrigez-moi si je me trompe, un trou noir de ce type a une densité proche de celle de l’air et exerce donc des forces de marée faibles dans l’environnement de son horizon des évènements, ce qui permet aux visiteurs de cette planète de ne pas être transformés en crêpes. Mais dans ce cas, s’il n’y a pas de recourbement fort de l’espace sur cette planète, comment le temps peut-il être lui très fortement ralenti ?
En vous remerciant
Parce que le “gel temporel” se manifeste au voisinage de l’horizon des événements d’un trou noir quelle que soit sa masse, et ne dépend pas des forces de marée, qui dans ce cas sont en effet très faibles…
Merci infiniment pour ces éclaircissements. Une autre question m’est venue en lisant le billet 2/6. Vous dites que la planète Miller doit orbiter à une vitesse proche de celle de la lumière. Et ce que ça implique là aussi un effet de distorsion temporelle relativement à la vitesse de rotation de la Terre ?
Encore merci.
En relisant plus attentivement vos billets, je crois pouvoir répondre Non à ma précédente question car ça n’est pas seulement la planète Miller qui tourne autour du trou noir mais une portion d’espace-temps (l’ergosphère ?) contenant la planète. Il n’y aurait donc pas d’effet relativiste dû à la vitesse de déplacement de cette planète.
Encore merci pour ce réenchantement de l’univers.
Time Dilation
Plane waves of a star light are coming from just above (frequency is constant). And these are hitting the roof of two passenger cars. In front of an observer, one is at a standstill, the other is moving horizontally.
Number of waves hitting the two cars per unit time is the same. There is no time dilation.
Sorry, I cannot receive E-mail. I do not have PC.
http://www.geocities.co.jp/Technopolis/2561/eng.html
Bonjour Mr Luminet,
L’équation que vous présentez rend donc possible une telle planète en rotation si proche autour d’un trou noir et avec une telle distorsion temporelle…
Mais en revoyant le film (et sans rien comprendre a cette équation), mon esprit septique par nature se demande
1 comment la planète peut ne pas être écartelée par les gradients de gravité d’une face a l’autre (je n’ai pas bien compris vos échanges sur le sujet)?
2 cette planète doit tourner bien vite, incommensurablement plus vite que le vaisseau d’où la navette se fait larguer en piquer. Ne faut il pas alors quelques 10, 100, ou 1000000 de tours à la navette pour rejoindre la planète au lieu d’un piqué ?
Bonjour Alex,
1. Les gradients de gravité engendrées par un trou noir supermassif (comme Gargantua dans le film) sont extrêmement faibles, contrairement à ceux engendrés par un trou noir de masse stellaire.
2. Je n’ai pas revu le film depuis sa sortie, ma mémoire a oublié cette scène et je ne puis vous répondre précisément, désolé.
Lorentz contraction
Plain waves of light (wavelength is constant) are coming from the upper right 45 degrees. Two bars of the same length are moving to the right and the left at the same speed. The number of waves hitting the bars is the same. Lorentz contraction is unthinkable. And also, time dilation will be denied.