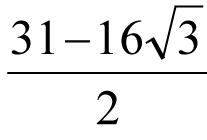L’un des problèmes pour construire des fortifications à l’époque de Vauban (1633 – 1707) était :
Comment défiler une fortification des tirs de l’ennemi ?
Le verbe « défiler » doit s’entendre ici au sens commun de « se défiler ». Comment cacher l’intérieur d’un ouvrage aux vues et aux tirs de l’agresseur ? Bien entendu, il suffit de bâtir partout des remparts assez hauts. L’ennui est que la hauteur fragilise les remparts. Le tout doit rester équilibré. Sur le terrain, les bons ingénieurs comme Vauban savaient défiler leurs ouvrages mais comment s’y prendre à partir d’un simple plan côté ?
La géométrie descriptive
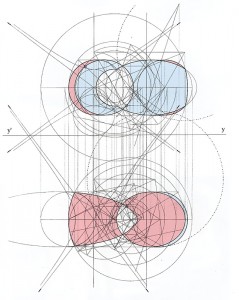
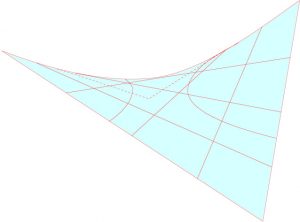
Gaspard Monge (1746 – 1818) inventa la géométrie descriptive pour résoudre ce problème. De façon générale, elle permettait d’étudier certains objets de l’espace comme l’intersection de deux tores dans l’épure qui suit. Le résultat pouvait être très esthétique, comme on peut le voir dans ce cas.
Les déblais et remblais
Le même Monge, sans doute également motivé par la construction de fortifications, publia un Mémoire sur la théorie des déblais et des remblais où il se proposait de résoudre un problème très concret : comment déplacer des tas de sable vers un certain nombre de destinations de la manière la plus économique possible ?
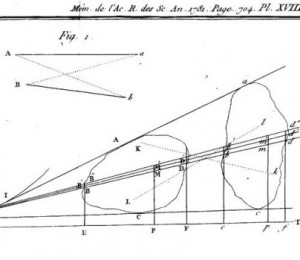
Ici il s’agit de déblayer la zone de gauche pour remblayer celle de droite (ou l’inverse puisque les deux problèmes sont équivalents). Dans son mémoire, Monge étudie ce problème mais ne le résout pas dans sa généralité. Voir l’article d’Étienne Ghys dans Image des mathématiques.
Le transport optimal
Ce problème se généralise en problème du transport optimal : comment un fournisseur peut-il livrer un certain nombre de points de vente de façon à minimiser ses coûts ? Le problème de Monge a ainsi été redécouvert par Léonid Kantorovitch (1912 – 1986) qui obtint le prix Nobel d’économie en 1975 pour ses avancées sur la question en ouvrant un nouveau domaine, celui de la programmation linéaire. Plus récemment, Cédric Villani (né en 1973) a obtenu la médaille Fields en revisitant le problème du transport optimal en le rapprochant du problème de la diffusion des gaz. Cette capacité de rapprochement entre des domaines a priori différents est un marqueur des grands mathématiciens.























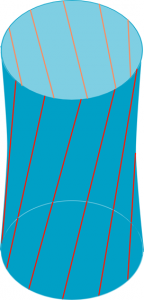
 Cette surface a été baptisée hyperboloïde de révolution à une nappe car elle est également obtenue en faisant tourner une hyperbole sur l’un de ses axes.
Cette surface a été baptisée hyperboloïde de révolution à une nappe car elle est également obtenue en faisant tourner une hyperbole sur l’un de ses axes.










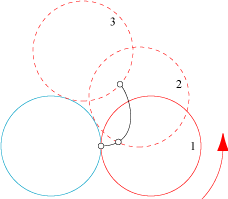


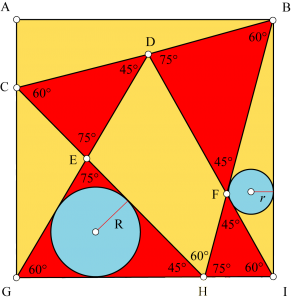
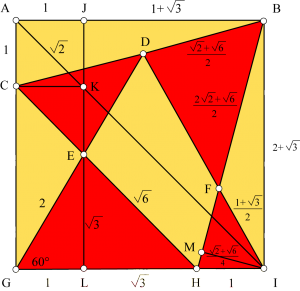
 Les deux triangles (rouge et vert) inscrits dans le carré jaune sont équilatéraux, quel est le rapport entre les rayons des cercles bleus ?
Les deux triangles (rouge et vert) inscrits dans le carré jaune sont équilatéraux, quel est le rapport entre les rayons des cercles bleus ?