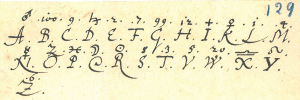Une carte postale adressée à une jeune fille nommée Léa chez ses parents le 27 janvier 1905 a de quoi surprendre car elle ne comporte que des nombres séparés de points ou de tirets.

Transcription de la carte
Le texte est constitué de nombres entre 2 et 25, qui représentent sans doute des lettres de l’alphabet, séparés par des points et des tirets. Les tirets séparent probablement les mots entre eux. Nous le reproduisons ici en remplaçant les tirets par des espaces :
25.22 21.2.8.8.24 7.22.4.19.2.20.20.24 25.2.23 5.24 12.9.24 17.24 18.22.23 24.5.4.23.18 17.24 20.22.14.22.23.8 4.23.24.20 4.24.5.9 19.24.7.9.23.8 2 17.2.9.4.8 17.22.23 23.9 18.24.8 2 5.22.4.18.24.8 5.24 25.22.18.23.20 17.24 20.22.23 4.23.24.20 24.9 22 17.22.14.24 8.23 18.9 8.22.14.22.23.8 5.2.25.25.24 17.24 8.9.23.8 23.25.7.22.18.23.24.20.18 12.9.22.20.19 24.13.13.24.8 8.2.20.18 24.20 4.24.18.22.4.19 22.9 4.24.14.2.23.4 25.2.20 22.20.21.24 22.19.2.4.24 18.2.9.18 22 18.2.23
Analyse
On remarque rapidement que le numéro 24 est majoritaire. Il représente sans doute le E. Un mot à l’avant dernière ligne se trouve alors à moitié décrypté. Il s’agit de 24.13.13.24.8. Le numéro 13 répété entre deux E ne peut être qu’une consonne, plus précisément L. On en déduit que ce mot est « elles ». Le suivant est alors probablement « sont ». Le chiffre s’écroule alors progressivement. En particulier la formule de politesse est « tout à toi ». Finalement, on obtient le texte :
Ma gosse, pardonne-moi ce que je t’ai écrit, je n’avais rien reçu depuis 2 jours. J’ai eu tes 2 cartes ce matin. Je n’ai rien eu à ja*e. Si tu savais comme je suis impatient quand elles sont en retard. Au revoir mon ange. Tout à toi.
L’étoile dans le texte est sans doute une erreur de chiffrement.