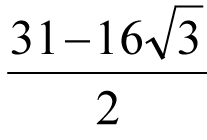Certaines croyances magiques restent attachées aux mathématiques. L’exemple le plus simple est celui du nombre treize qui porte chance … ou malchance selon les personnes. On évite ainsi, même chez certains mathématiciens, d’être treize à table. Cette croyance est extra-mathématique. Elle vient du dernier repas du Christ avec ses apôtres et non pas d’une propriété mathématique du nombre treize. Il en est de même de la plupart des nombres considérés comme magiques ou sacrés, comme sept par exemple. Nous n’insisterons pas sur cette question, et pas davantage sur la numérologie ou sur l’arithmancie qui prétendent prévoir l’avenir au travers de quelques additions. Leurs relations aux mathématiques sont les mêmes que celle de l’astrologie à l’astronomie. Même si certains mathématiciens furent numérologues comme certains astronomes furent astrologues jusqu’à l’époque de Kepler (XVIIe siècle), aujourd’hui, il est difficilement imaginable qu’un mathématicien ou un astronome pratique ce type de pseudosciences.
Les nombres parfaits
Plus étonnants que ces nombres auxquels on attribue un pouvoir surnaturel, d’autres sont considérés comme magiques pour des raisons internes aux mathématiques. Parmi les plus étudiés sont les nombres parfaits dont parle déjà Euclide au IIIe siècle avant notre ère dans ses Éléments. Par définition, les nombres parfaits sont les nombres égaux à la somme de leurs diviseurs autres qu’eux-mêmes. Par exemple, 6 est parfait puisque ses diviseurs stricts sont 1, 2 et 3 dont la somme est égale à 6. La traduction littérale du terme grec utilisé par Euclide pour désigner les nombres parfaits est nombre à qui il ne manque rien ce qui permet de mieux comprendre les définitions de nombre abondant et de nombre déficient : nombre dont la somme des diviseurs est supérieure (respectivement inférieure) au nombre donné. Ainsi 12 est abondant, 3, 4 et 5 sont déficients.
Quand Dieu est contraint à la perfection …

Cela pourrait être une simple curiosité et peu importe le nom utilisé mais, dans l’Antiquité, la perfection de ces nombres était bien vue comme telle. Ainsi, dans La cité de Dieu, on peut lire sous la plume d’Augustin d’Hippone (354 – 430) une vision mystique de cette perfection : Ainsi, nous ne devons pas dire que le nombre six est parfait, parce que Dieu a achevé tous ses ouvrages en six jours : loin de là, Dieu a achevé tous ses ouvrages en six jours parce que le nombre six est parfait ; supprimez le monde, ce nombre resterait également parfait ; mais s’il n’était pas parfait, le monde, qui reproduit les mêmes rapports, n’aurait plus la même perfection.
On trouve des idées voisines dans Arithmetica d’un philosophe néo-pythagoricien comme Nicomaque de Gérase (Ier siècle de notre ère), pourtant véritable mathématicien puisqu’il découvrit le quatrième nombre parfait : Il arrive que, de même que le beau et le parfait sont rares et se comptent aisément, tandis que le laid et le mauvais sont prolifiques, les nombres excédents et déficients sont en très grand nombre et en grand désordre ; leur découverte manque de toute logique. Au contraire, les nombres parfaits se comptent facilement et se succèdent dans un ordre convenable ; on n’en trouve qu’un seul parmi les unités, 6, un seul dans les dizaines, 28, un troisième assez loin dans les centaines, 496 ; quant au quatrième, dans le domaine des mille, il est voisin de dix mille, c’est 8128. Ils ont un caractère commun, c’est de se terminer par un 6 ou par un 8, et ils sont tous invariablement pairs.
Des conjectures à la pelle
À l’heure actuelle, le dernier point évoqué par Nicomaque de Gérase reste une conjecture. Personne n’a encore réussi à prouver qu’il n’existait pas de nombres parfaits impairs, même si le fait que personne n’en ait jamais trouvé un seul milite dans ce sens. De même, l’existence d’une infinité de nombres parfaits pairs est une conjecture. Les quatre premiers sont connus depuis l’Antiquité : 6, 28, 496 et 8128 et, à l’heure actuelle, nous n’en connaissons que 49 ! Les plus grands n’ont été découverts que récemment et ont plusieurs dizaines de millions de chiffres. Ils sont tous d’une forme liée à la notion de nombre premier, ce que nous verrons plus loin.
Les temps ont changé et plus personne ne comprend l’expression « nombre parfait » dans le sens d’une perfection externe aux mathématiques.















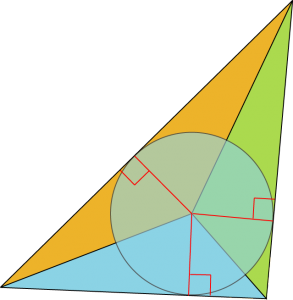
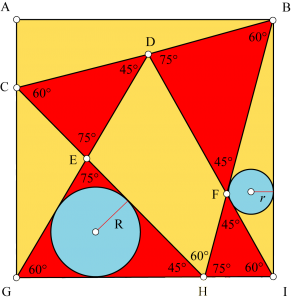
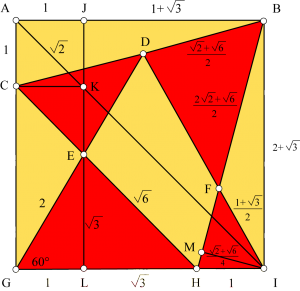
 Les deux triangles (rouge et vert) inscrits dans le carré jaune sont équilatéraux, quel est le rapport entre les rayons des cercles bleus ?
Les deux triangles (rouge et vert) inscrits dans le carré jaune sont équilatéraux, quel est le rapport entre les rayons des cercles bleus ?