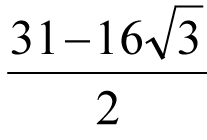Archives pour la catégorie Graphismes

Arts, Graphismes, Mathématiques, Photographies, Sciences

Les maths et la matière

Laisser un commentaire

Toujours à la recherche d’œuvres d’art inspirées par les mathématiques, et la science en général, j’ai découvert dans une petite galerie d’art parisienne (galerie Sonia Monti, Paris VIII), quelques œuvres de François Sforza, dont l’originalité est d’allier les maths et la matière.

La formule d’Euler

Leonhard Euler (1707 – 1783) est l’auteur d’une formule déclarée “plus belle formule des mathématiques” en plusieurs occasions :

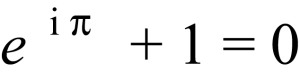
Pourquoi si belle ? La raison souvent invoquée est la réunion de cinq constantes fondamentales : les éléments neutres de l’addition (0) et de la multiplication (1), la mystérieuse racine carrée de -1 (i) et les deux nombres transcendants les plus rencontrées (e et pi). François Sforza suggère de plus une démonstration élémentaire de la formule sur son tableau.

Lidentité d’Euler par François Sforza. La photo ne reflète  pas la matière de la peinture.

Dans un autre post, j’ai célébré cette même formule dans une autre matière : le verre.

La plus belle formule des mathématiques

L’hypothèse de Riemann

La fonction zêta de Riemann est à l’honneur dans une autre toile, accompagnée de son lien avec les nombres premiers, dû à Euler.

Fonction zêta par François Sforza. Au cœur de l’hypothèse de Riemann.

L’hypothèse de Riemann se trouve de façon étonnante au salar d’Uyuni en Bolivie, taguée sur une locomotive rouillée :

L’hypothèse de Riemann au salar d’Uyuni

Pour finir, voici quelques autres peintures de François Sforza.

L’inconnue de François Sforza.
Synaptik par François Sforza. Une plongée imaginaire dans notre cerveau où des formules mathématiques remontent le long des neurones.

 

Vibration sonore par François SforzaPour en savoir plus sur l’artiste

https://sforzafrancois.portfoliobox.net

 

Arts, Graphismes, Histoire, Humour, Mathématiques

Cercle qui roule se quarre

Laisser un commentaire

La quadrature du cercle consiste à construire un carré de même aire qu’un cercle donné. Si le cercle a pour rayon R, il s’agit donc de construire un carré de côté R multiplié par la racine carrée du nombre Pi. On peut donc réaliser la quadrature du cercle avec une règle graduée à la précision que l’on veut.

Des règles qui changent tout

Quand le problème est apparu dans l’Antiquité, il n’était pas question d’approximations, la règle était que la construction devait être exacte. Il en existe plusieurs. L’une d’entre elle demande de faire rouler un cercle sur une droite. La voici sous forme de tableau :

Le cercle part de la position à gauche (en rouge) pour arriver à celle de droite (en jaune) ce qui permet de définir le carré de droite, de même aire que le cercle initial.

En utilisant uniquement le théorème de Pythagore, on démontre que le carré est de côté racine de Pi, ce qui prouve que le carré et le cercle ont même aire (voir à la fin pour une démonstration).

Cette utilisation d’un procédé mécanique (faire rouler le cercle) ne convenait pas aux anciens, il fallait construire le carré à la règle (non graduée) et au compas. Dans ces conditions, le problème devient impossible, ce qui n’a été prouvé qu’au XIX-ième siècle en démontrant que le nombre Pi est transcendant c’est-à-dire qu’il n’est pas solution d’une équation algébrique à coefficients entiers.

De façon étonnante, un problème purement géométrique et très conditionné par des visions antiques a eu des conséquences importantes en algèbre et en analyse.

Un peu de géométrie

La figure essentielle est la suivante :

Il s’agit de montrer que HC a pour longueur la racine carrée de Pi.

En appliquant le théorème de Pythagore dans les trois triangles rectangles HBC, HC et ABC, on obtient :

HC² + 1 = BC², HC²+ Pi² = AC² et BC² + AC² = (Pi + 1)²

En faisant la somme des deux premières expressions puis un peu d’algèbre, il vient que HC² est égal à Pi ce qu’il fallait démontrer.

Une lampe pour une idée lumineuse

Cette quadrature du cercle, dont l’auteur initial nous est inconnu, m’a inspiré la lampe suivant :

Cercle qui roule se quarre par Hervé Lehning.
Arts, Graphismes, Histoire, Mathématiques, Vie quotidienne, Voyages

L’art du défilement, Vauban et Gaspard Monge

Laisser un commentaire

L’un des problèmes pour construire des fortifications à l’époque de Vauban (1633 – 1707) était  :

Comment défiler une fortification des tirs de l’ennemi ?

Le verbe « défiler » doit s’entendre ici au sens commun de « se défiler ». Comment cacher l’intérieur d’un ouvrage aux vues et aux tirs de l’agresseur ? Bien entendu, il suffit de bâtir partout des remparts assez hauts. L’ennui est que la hauteur fragilise les remparts. Le tout doit rester équilibré. Sur le terrain, les bons ingénieurs comme Vauban savaient défiler leurs ouvrages mais comment s’y prendre à partir d’un simple plan côté ?

La géométrie descriptive

Gaspard Monge (1746 – 1818) inventa la géométrie descriptive pour résoudre ce problème. De façon générale, elle permettait d’étudier certains objets de l’espace comme l’intersection de deux tores dans l’épure qui suit. Le résultat pouvait être très esthétique, comme on peut le voir dans ce cas.

Dessin se trouvant dans Objets mathématiques, Institut Henri Poincaré, livre que nous recommandons fortement.

Les déblais et remblais

Le même Monge, sans doute également motivé par la construction de fortifications, publia un Mémoire sur la théorie des déblais et des remblais où il se proposait de résoudre un problème très concret : comment déplacer des tas de sable vers un certain nombre de destinations de la manière la plus économique possible ?

Dessin explicatif du problème dans le mémoire de Monge.

Ici il s’agit de déblayer la zone de gauche pour remblayer celle de droite (ou l’inverse puisque les deux problèmes sont équivalents). Dans son mémoire, Monge étudie ce problème mais ne le résout pas dans sa généralité. Voir l’article d’Étienne Ghys dans Image des mathématiques.

Le transport optimal

Ce problème se généralise en problème du transport optimal : comment un fournisseur peut-il livrer un certain nombre de points de vente de façon à minimiser ses coûts ? Le problème de Monge a ainsi été redécouvert par Léonid Kantorovitch (1912 – 1986) qui obtint le prix Nobel d’économie en 1975 pour ses avancées sur la question en ouvrant un nouveau domaine, celui de la programmation linéaire. Plus récemment, Cédric Villani (né en 1973) a obtenu la médaille Fields en revisitant le problème du transport optimal en le rapprochant du problème de la diffusion des gaz. Cette capacité de rapprochement entre des domaines a priori différents est un marqueur des grands mathématiciens.

 

Énigmes, Graphismes, Histoire, Nature, Photographies, Regard sur le monde, Voyages

L’hypothèse de Riemann au salar d’Uyuni

Laisser un commentaire

Le salar d’Uyuni est un gigantesque désert de sel sur les hauts plateaux boliviens. On y trouve un cimetière de locomotives offrant plusieurs nuances de rouilles du meilleur effet photographique.

Locomotive rouillant sur le salar d’Uyuni

Un tag étonnant

Une grande partie de ce matériel ferroviaire à l’abandon est tagué. Une inscription nous a tout de même étonné par sa composante mathématique.

L’hypothèse de Riemann taguée sur une locomotive rouillant dans le salar d’Uyuni

Le tag affirme que les zéros non triviaux (i.e. entiers négatifs pairs) de la fonction dzéta de Riemann sont complexes de partie réelle égale à 1/2. Il s’agit d’une conjecture faite par Bernhard Riemann en 1859 et aujourd’hui dotée d’un prix d’un million de dollars par l’institut Clay. Rencontre étonnante !

 

Arts, Énigmes, Graphismes, Mathématiques, Voyages

Une sangaku célèbre, de Hidetoshi Fukagawa

4 commentaires

Les sangakus japonaises sont de petits chefs d’œuvres aussi bien au niveau du raisonnement mathématique que de l’esthétique. Jean Constant, par exemple, s’en est fait une spécialité (voir l’image mise en avant). La sangaku suivante a été découverte par Hidetoshi Fukagawa.

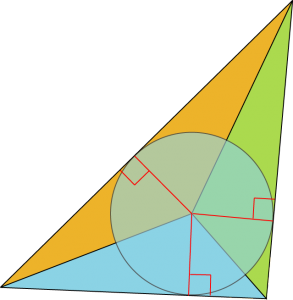
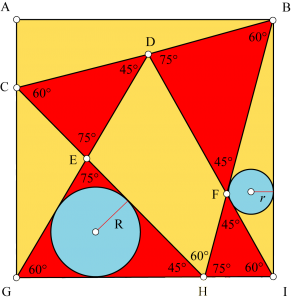
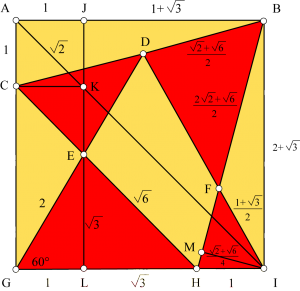
Les deux triangles (rouge et vert) inscrits dans le carré jaune sont équilatéraux, quel est le rapport entre les rayons des cercles bleus ?

Rayon d’un cercle inscrit

Les deux cercles sont inscrits dans deux triangles. Un théorème permet d’en calculer les rayons en fonction de leurs aires et de leurs périmètres. Plus précisément, le rayon du cercle inscrit dans un triangle est égal à deux fois la surface du triangle divisé par son périmètre, ce résultat est mis en évidence par un dessin : l’aire du triangle se décompose en  trois triangles de même hauteur, le rayon du cercle inscrit. L’aire de chacun de ces triangles est donc égale au rayon du cercle inscrit multiplié par la longueur du côté opposé divisée par deux. En faisant la somme, le périmètre du triangle s’introduit naturellement .

Plan d’attaque du problème

Pour calculer les rayons des deux cercles, il s’agit donc de calculer un certain nombre de longueurs de segments de la figure. L’idée pour les calculer vient si nous en oublions une partie. En utilisant les angles de 60° et de 45° en évidence, nous trouvons que les triangles rouges ont les mêmes angles et sont donc semblables.

Grâce aux rapports de similitude et au théorème de Pythagore, les mesures de longueurs apparaissent progressivement, une d’entre elles (AC) ayant été choisie comme unité. Le dessin est utile pour suivre le raisonnement. Nous en déduisons progressivement les diverses longueurs importantes. Elles sont notées sur le dessin ci-dessous.

On en déduit les valeurs des deux rayons :

Un calcul algébrique

Un calcul algébrique permet de montrer que R = 2 r. Pour cette dernière étape, aucune visualisation n’est nécessaire et nous pouvons l’exécuter avec un logiciel de calcul formel. Ce dernier calcul nous entraîne vers les extensions algébriques, nous nous arrêterons à leur porte.

L’éventail de la geisha

Dans certaines sangakus, les auteurs ont clairement privilégié l’esthétique.

Par exemple, dans celui en forme d’éventail ouvert aux deux tiers ci-dessus, il s’agit de trouver le rapport entre les rayons des cercles verts et rouges. Ici encore, l’essentiel est d’introduire les bons points, qui ne sont pas directement visibles. On trouve :

 

Arts, Graphismes, Mathématiques

Les surfaces minimales de Patrice Jeener

Laisser un commentaire

Patrice Jeener est un graveur tombé amoureux des mathématiques en visitant l’institut Henri Poincaré quand il était étudiant aux beaux-arts. Il suivait ainsi la trace de Man Ray, qui découvrit les modèles de l’institut dans les années 30 et s’en inspira pour sa série de tableaux équations shakespeariennes comme celui-ci intitulé le roi Lear :

Le roi Lear © Man Ray

Les surfaces minimales

Patrice Jeener s’est particulièrement intéressé aux surfaces minimales, c’est-à-dire aux surfaces dont les aires sont minimales pour un bord donné. On peut matérialiser la plupart d’entre elles par des bulles de savon s’appuyant sur un contour, car le film de savon tend à minimiser son énergie, donc sa surface. Elles ont des applications pratiques mais notre propos n’est pas là. Sur la photographie ci-dessous, notez la petite tige en bas à droite qui permet de tenir l’objet quand on le trempe dans l’eau savonnée :

Nous n’écrirons pas leurs équations ici, nous nous contenterons d’en admirer l’esthétique à travers quelques gravures.

Surface minimale de Schwartz © Patrice Jeener

L’étude des surfaces réservent quelques surprises comme l’apparition surprenante d’une chouette là où l’on attendait une simple surface minimale. Ce genre de surprises explique sans doute ce vers de Lautréamont :

O mathématiques sévères, je ne vous ai pas oubliées, depuis que vos savantes leçons, plus douces que le miel, filtrèrent dans mon cœur, comme une onde rafraîchissante.

Surface minimale à la chouette © Patrice Jeener
Graphismes, Mathématiques

Décrypter l’art concret

Laisser un commentaire

Philippe Leblanc a exposé chez Philomuses, au quartier latin à Paris, une série d’œuvres a priori abstraites. Les titres même font mystère. Par exemple, la suivante se nomme Chinacci 25.

Chinacci 25 © Philippe Leblanc

L’écriture chinoise ancienne des nombres

En lisant le tableau en colonne, le mathématicien sera frappé par la régularité des premiers termes : 1, 1, 2, 3, 5 où chaque nombre est la somme des deux précédents. Le suivant peut facilement être interprété comme un 8. De fait, le tableau de Philippe Leblanc utilise un système d’écriture des nombres inventé en Chine quelques siècles avant Jésus-Christ. À cette époque, les Chinois comptaient au moyen de baguettes et non de bouliers comme plus tard. Ils imaginèrent ainsi une façon d’écrire les nombres. Pour cela, ils utilisaient deux notations qu’ils alternaient pour éviter les confusions entre unités, dizaines, centaines, etc. Voici donc les chiffres de 1 à 9 écrits de deux façons différentes.

La suite de Fibonacci

On s’aperçoit ainsi que le tableau représente les 25 premiers termes de la suite de Fibonacci, le dernier terme en bas à droite du tableau valant 75025. Le titre de l’œuvre prend alors son sens, Chinacci 25 étant une contraction de Chinois-Fibonacci, 25 premiers termes. Après cette première analyse, on peut se demander ce que signifient les différences de couleurs, entre jaune et bleu. Pour le voir, il faut réaliser que les bâtons de l’œuvre sont découpés au laser dans une tôle d’acier, qui cache une boîte lumineuse. C’est le fond de cette boîte qui est peinte selon plusieurs bandes verticales dont les largeurs suivent également la suite de Fibonacci : une bande de largeur X en jaune, une deuxième bande de largeur X en bleu foncé, une bande de largeur 2X en jaune orangé, une quatrième bande de largeur 3X en bleu clair. La deuxième œuvre Mayanacci 25  s’éclaire alors d’elle-même.

Mayainacci 25 © Philippe Leblanc

La suite de Fibonacci s’y écrit en lignes puisque la première se lit 1, 1, 2, 3 en comptant les points. La barre qui suit signifie alors probablement 5. On peut ainsi décrypter les nombres suivants. Il s’agit en fait de l’écriture des nombres qu’utilisaient les Mayas, en base vingt. Les unités, les vingtaines, etc. s’empilent de bas en haut. Les couleurs respectent une règle différente de celle du tableau précédent puisque, dans chacune des cinq lignes et des cinq colonnes, on trouve une et une seule fois chacune des cinq couleurs présentes.