Les forts du Moyen-Âge peuvent avoir des formes polygonales. Celles-ci restent cependant convexes. La règle pour les forts de l’époque de Vauban est différente. En terrain plat, on part d’un polygone régulier convexe. La longueur des côtés correspond à la portée utile des pièces d’artillerie de l’époque, un peu moins pour que l’effet soit meilleur. La norme est de 330 mètres. Le nombre de côtés dépend alors de la taille de la ville à ceinturer ainsi. Par exemple, un pentagone régulier de côté égal à 330 mètres englobe une surface de 18 hectares, un hexagone, 28 et un octogone, 52.

Partons ici d’un pentagone comme pour la citadelle de Lille. Au milieu de chaque côté, perpendiculairement et vers l’intérieur, nous portons une longueur de 55 mètres. Nous obtenons, un polygone plus compliqué en forme d’étoile.

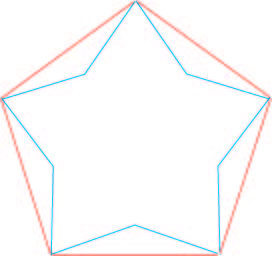
Ajout des bastions

Le but est d’établir aux sommets du polygone initial de petits fortins appelés « bastions » et destinés à recevoir des pièces d’artillerie pouvant couvrir les côtés du polygone en étoile, appelés « courtines ». Pour éviter d’être de trop bonnes cibles pour l’artillerie adverse, ces remparts ne dépassent pas du paysage. Leur hauteur vient des fossés situés autour. Ces murs sont essentiellement constitués de terre pour mieux résister aux boulets en fer. La maçonnerie qui les entoure est destinée à tenir le tout. Du côté de la place forte, elle se nomme l’escarpe. De l’autre côté, la contrescarpe. Un domaine est laissé vide et sans protection pour l’ennemi tout autour. Il se nomme le glacis. Sa longueur correspond au minimum à la portée des canons. Vu du glacis, l’assaillant n’aperçoit que des murailles modestes puisque le fossé les dissimule.

Nous sommes maintenant en présence de plusieurs polygones, l’un extérieur joignant les extrémités des bastions, l’autre intérieur dans le prolongement des courtines. Un autre limite le glacis.

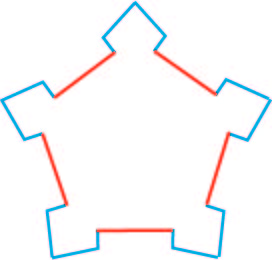
Multiplication des défenses externes

Pour éviter ce défaut, Vauban a l’idée d’ajouter deux défenses externes devant chaque courtine : la tenaille à son pied et la demi-lune devant. Chacune de ces défenses n’offre aucune protection du côté de la place forte elle-même. Si l’ennemi la prend, il s’y trouve à découvert, donc dans une position difficile à tenir.

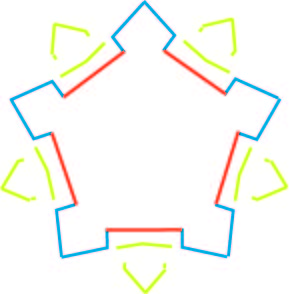
Vauban généralisa ce principe en détachant les bastions de la place forte elle-même. D’autre part, le tout est entouré d’un dernier petit rempart parallèle et recouvert, appelé « chemin couvert ». Ainsi, il se situe au sommet de la contrescarpe. Il s’agit en même temps de la première ligne de défense et d’un chemin de ronde, destiné à l’observation.