A Boukhara, en Ouzbékistan, une étrange construction fait face à l’antique forteresse. Ce monument, qui n’attire pas les touristes, est pourtant témoin d’un courant artistique important du début du vingtième siècle : le constructivisme russe.
Un château d’eau
Cette tour a été construite en 1927 par Vladimir Choukhov (1853 – 1939) pour servir de château d’eau. Désaffecté à la fin des années quarante, il est alors devenu un café jusqu’à ce qu’un accident mortel interdise cet usage. Il vient d’être racheté par des Français pour devenir un point d’observation. Un ascenseur est prévu pour y accéder.

Un hyperboloïde de révolution
La surface utilisée par Choukhov est célèbre en mathématiques et en architecture car elle est construite avec des droites. Pour comprendre sa fabrication, le plus simple est de partir d’un cylindre, une surface simple à construire. Pour cela, il suffit de prendre un axe, d’y monter deux roues et d’y tendre des élastiques parallèles à l’axe. On obtient l’objet suivant.
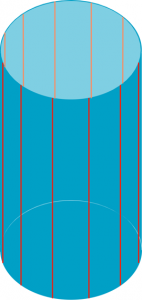
Les droites représentées par les élastiques sont les génératrices du cylindre.
On fait alors tourner la roue du haut d’un certain angle dans un sens et celle du bas du même angle dans le sens opposé. On obtient une nouvelle surface également générée par des droites.
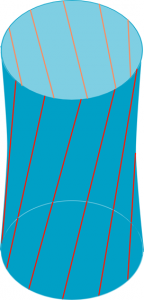
Il se trouve qu’en tordant le cylindre du même angle dans un sens ou dans l’autre, on obtient la même surface, qui possède ainsi deux familles de génératrices.
 Cette surface a été baptisée hyperboloïde de révolution à une nappe car elle est également obtenue en faisant tourner une hyperbole sur l’un de ses axes.
Cette surface a été baptisée hyperboloïde de révolution à une nappe car elle est également obtenue en faisant tourner une hyperbole sur l’un de ses axes.
Pour des raisons physiques, cette surface est utilisée pour les tours de refroidissement des centrales nucléaires ou thermiques.
Les tabourets népalais
Cette surface est utilisée au Népal pour construire des tabourets avec des morceaux de bambous de longueurs égales.

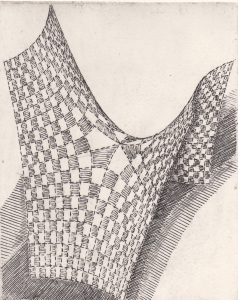
L’hyperboloïde à une nappe vu par Patrice Jeener
Patrice Jeener, surnommé le graveur d’équations, s’est inspiré de cette surface :
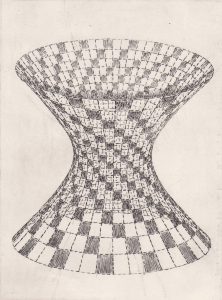
Sur ce dessin, on voit particulièrement bien l’hyperbole qui génère l’hyperboloïde par rotation autour de l’un de ses axes. En changeant d’axe, on obtient un
L’hyperboloïde à deux nappes :
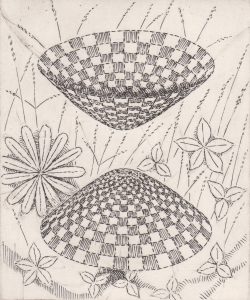
Les fleurs sur ce deuxième dessin sont également des objets mathématiques qu’affectionne Patrice Jeener. Dans son œuvre, on trouve une surface apparentée, également engendrée par deux familles de droites : le paraboloïde hyperbolique :
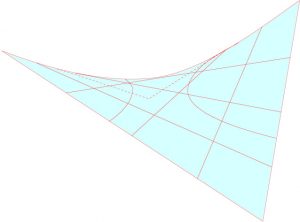
Construction du paraboloïde hyperbolique
La méthode utilisée pour construire l’hyperboloïde peut l’être en remplaçant le cylindre par un plan. Autrement dit, on garde le dispositif initial : axe et roues mais, au lieu de tendre les élastiques entre les deux roues, on les tend entre deux rayons parallèles, avant de tourner les roues. On obtient une nouvelle surface admettant deux familles de droites génératrices comme la précédente, il s’agit du paraboloïde hyperbolique.
Cette surface est utilisée en architecture pour fabriquer des toits. Le Corbusier et Iannis Xenakis (le musicien dont on oublie souvent qu’il fut architecte ont ainsi construit le pavillon Philips pour l’exposition universelle de Bruxelles en 1958.

