Archives pour l'étiquette énigme

géométrie, Mathématiques

L’angle mystérieux

Un commentaire

On donne la configuration suivante où le triangle OAB est isocèle et les angles lambda = 20°, alpha = 60° et bêta = 50° sont donnés.

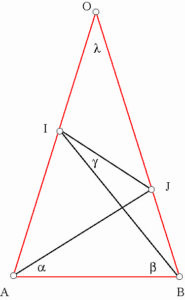
La figure est volontairement fausse;

Il s’agit de trouver la valeur de gamma.

Faire un dessin correct

Le dessin fourni est grossièrement faux. En vous appliquant avec une règle et un rapporteur, vous trouverez 80°, à moins que cela un nombre très proche bien sûr. Comment savoir ? Pour cela une seule solution : il faut le prouver !

Pour essayer de le faire, vous utiliserez sans doute les relations angulaires classiques (somme des angles d’un triangle, angles opposés, etc.) pour déterminer le plus d’angles possibles. Quoique vous fassiez, vous n’atteindrez pas l’angle cherché de cette façon. Il reste pourtant que cet angle est bien entièrement déterminé.

L’introduction d’un cercle

La notion d’angle est intimement liée aux cercles, il est donc naturel d’en introduire un. C’est donc assez logiquement que nous introduisons le cercle de centre O passant par A et B ce qui nous mène à la figure suivante :

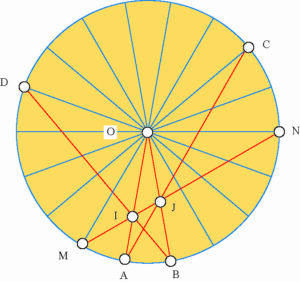
Si on construit le polygone régulier de centre O et d’angle au centre AOB, on s’aperçoit que la droite IJ semble couper le cercle en deux points du polygone M et N. De même AJ et BI en C et D.

Admettons que nous ayons réussi à le prouver, en utilisant les relations dans le triangle OIN, nous trouvons :

OIN = 180 – ONM – ION

Or, en utilisant les angles au centre ainsi que les angles inscrits :

ONM = 30 et ION = 100 donc OIN = 50. On en déduit le résultat.

Le nœud de la preuve

Il reste donc à prouver que la droite IJ coupe effectivement le cercle en M et N. Nous pouvons oublier les points C et D puisqu’ils n’interviennent pas pour démontre le résultat final. Il s’agit donc de montrer que les points du polygone M et N et les points I et J sont alignés.

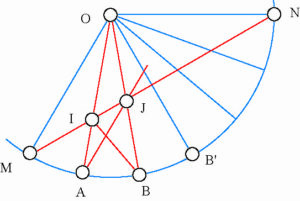
Pour cela, on constate d’abord que le triangle OAJ est isocèle (angles en O et A égaux à 30° donc OJ = JA. D’autre part, JA = JB’ par symétrie donc OJ= JB’ d’où l’on déduit que J appartient à la médiatrice de OB’ c’est-à-dire  à MN.

Enfin IMA = IBA = 50° (symétrie) et de même NMA = 50° (angle inscrit. Il en résulte que I appartient à MN. Nous avond démontré que les quatre points M, N, I et J sont alignés. Le résultat s’ensuit.

Énigmes, Histoire, Mathématiques

Les pesées de Leibniz et de Bachet

Laisser un commentaire

Voici une question autrefois pratique, qui reste aujourd’hui ludique. Elle suppose l’utilisation d’une balance de Roberval, qui fut inventée par Gilles Personier de Roberval (1602 –  1675). Nous en donnons le schéma mais, pour comprendre l’usage que l’on en fait, il suffit de savoir que les deux plateaux s’équilibrent quand les masses qui s’y trouvent sont égales.

Schéma d’une balance de Roberval. Le parallélogramme articulé aux quatre sommets (en rouge) peut pivoter autour du point marqué (en blanc) sur la figure. L’aiguille est dirigée verticalement quand les poids sur les plateaux s’équilibrent.

Pesée binaire de Leibniz

Leibniz a montré que, si on dispose d’une série de poids dont chacun est le double du précédent, on peut réaliser toutes les pesées possibles. Pour voir comment, imaginons un objet de 713 grammes à peser avec des poids de 1, 2, 4, 8, 16, 32, 64, 128, 256 et 512 grammes. L’objet étant dans un plateau, nous commençons par placer le plus gros poids possible, c’est-à-dire celui de 512 grammes dans l’autre. Nous recommençons ensuite itérativement jusqu’à l’équilibre.

Voyons les étapes de ce processus. Le déficit est de 713 – 512 = 201 grammes. Nous utilisons alors le poids de 128 grammes (le plus gros possible). Il reste 201 – 128 = 73 grammes. Après le poids de 64 grammes, il ne reste plus que 9 grammes. Nous terminons en décomposant 9 en 8 + 1. Finalement, nous avons équilibré le poids de 713 grammes avec les poids prévus. D’un point de vue arithmétique, cela s’écrit :

713 = 512 + 128 + 64 + 8 + 1.

Ce résultat correspond à l’écriture de 713 en base deux : 713 = 29 + 27 + 26 + 23 + 20 ce que l’on peut noter : 1011001001. En base dix, nous écrivons : 713 = 7.102+ 101+ 3.100. La différence apparente est que l’écriture en base deux n’implique que des additions, pas de multiplication. En fait, il n’en est rien puisque les chiffres en base deux sont seulement 0 et 1 au lieu de 0, 1, …, 9. La propriété est générale, notre démarche prouve d’ailleurs que tout nombre s’écrit en binaire.

Pesée ternaire de Bachet

À l’occasion d’une récréation mathématique, Claude Bachet de Mériziac (1581 – 1638) a montré que, à condition d’utiliser les deux plateaux, on peut peser n’importe quel objet à l’aide d’une série de poids dont chacun est le triple du précédent. Voyons comment sur l’exemple précédent et des poids de 1, 3, 9, 27, 81, 243 et 729 grammes. L’idée précédente fonctionne si on dispose de deux poids de chaque sorte. Il suffit d’écrire 713 en ternaire. On commence par retrancher deux fois 243 à 713, il reste 227. On recommence avec deux fois 81, il reste 65. On retranche alors deux fois 27, il reste 11 ce qui fait 9 plus deux fois 1. Cette suite d’opérations fournit l’écriture ternaire : 222102 ce que l’on peut écrire : 713 = 2.35 + 2.34 + 2.33 + 32 + 2.30. Pour conclure, l’idée essentielle est d’éliminer les 2 du membre de droite de cette égalité en remarquant que : 3 = 2 + 1. Plus précisément : 713 + 35 + 34 + 33 + 30 = 36 + 35 + 34 + 32 + 31 ce qui se simplifie en : 713 + 33 + 30 = 36 + 32 + 31, c’est-à-dire en : 713 + 27 + 1 = 729 + 9 + 3. Il suffit donc de disposer des poids de 27 et 1 grammes dans le plateau de gauche et de 729, 9 et 3 grammes dans celui de droite.