Suite du billet précédent Les passages de Mercure (1/2) : de Kepler à Gassendi et fin
Après la première observation du transit de Mercure du 7 novembre 1631 par Pierre Gassendi, les passages suivants vont susciter un intérêt astronomique de plus en plus grand. Celui du 9 novembre 1644 est toutefois invisible en Europe. Idem pour celui du 3 novembre 1651, mais il est observé par Jeremy Shakerley à Surat (Inde). Le passage du 3 mai 1661 est observé par le célèbre Hevelius à Dantzig (Gdansk), en Pologne. Celui du 4 novembre 1664 n’est pas documenté, et celui du 7 novembre 1674 est invisible en Europe.
N’arrêtez pas votre lecture à cette fastidieuse énumération : le cours de l’histoire de l’astronomie va changer avec le transit de Mercure du 7 novembre 1677 ! Voici pourquoi.
La distance Terre-Soleil par la méthode des transits
La troisième loi du mouvement planétaire formulée par Kepler en 1618, qui donne une relation entre la période de révolution d’une planète et le demi-grand axe de son orbite, permet de connaître la taille du système solaire à un facteur d’échelle près. La connaissance d’une seule distance entre planètes ou entre une planète et le Soleil suffit donc pour calculer toutes les autres.
La parallaxe solaire est l’angle sous lequel on voit le rayon de la Terre depuis le Soleil. La connaissance de la parallaxe est donc équivalente à la connaissance de la distance Terre-Soleil.
 Le problème pratique est que l’angle est si petit qu’il est extrêmement difficile à mesurer (on sait aujourd’hui qu’il est égal à 8,794 secondes d’arc, soit 1/200 le diamètre apparent de la Lune). Les mesures et calculs effectués depuis l’Antiquité surestimaient considérablement cet angle, donc sous-estimaient la valeur réelle de la distance Terre-Soleil.
Le problème pratique est que l’angle est si petit qu’il est extrêmement difficile à mesurer (on sait aujourd’hui qu’il est égal à 8,794 secondes d’arc, soit 1/200 le diamètre apparent de la Lune). Les mesures et calculs effectués depuis l’Antiquité surestimaient considérablement cet angle, donc sous-estimaient la valeur réelle de la distance Terre-Soleil.

Or, en 1677, sur l’île de Sainte-Hélène où il s’est rendu pour établir un catalogue des étoiles du ciel austral, le grand astronome anglais Edmund Halley (1656-1742) observe le passage de Mercure qui a lieu le 7 novembre. Il bénéficie d’un beau temps inespéré, et d’une durée de transit de 5h 14m. De retour en Angleterre, Halley imagine une méthode simple mais géniale pour déterminer la parallaxe solaire. Sa méthode est basée sur la comparaison des temps de transit de Mercure ou de Vénus, mesurés depuis plusieurs lieux terrestres situés à des latitudes différentes. La différence des temps de passages observés donne accès à la parallaxe du Soleil. On remplace ainsi une difficile mesure de très petit angle par des mesures de temps.
 Halley estime cependant que les passages de Vénus seront plus profitables que ceux de Mercure, la planète étant plus grosse, moins rapide et plus proche de la Terre que Mercure. En outre les passages de Mercure, bien que plus fréquents, sont plus difficiles à observer. Les passages suivants de Vénus devant se produire en 1761 et 1769, Halley laisse à ses successeurs le soin de réaliser les observations et d’appliquer sa méthode. Ses prédictions et recommandations sont publiées dans les Philosophical Transactions of the Royal Society of London en 1691, 1694 et 1716.
Halley estime cependant que les passages de Vénus seront plus profitables que ceux de Mercure, la planète étant plus grosse, moins rapide et plus proche de la Terre que Mercure. En outre les passages de Mercure, bien que plus fréquents, sont plus difficiles à observer. Les passages suivants de Vénus devant se produire en 1761 et 1769, Halley laisse à ses successeurs le soin de réaliser les observations et d’appliquer sa méthode. Ses prédictions et recommandations sont publiées dans les Philosophical Transactions of the Royal Society of London en 1691, 1694 et 1716.
La méthode de Halley consiste à mesurer le temps écoulé entre le premier et le dernier contact intérieur de l’astre avec le disque solaire en au moins deux lieux ayant le plus grand écart possible en latitude. Pour cela, on doit se rendre sur des lieux d’observation souvent très éloignés et l’on doit effectuer en ces lieux des observations préliminaires de manière à déterminer avec précision leurs coordonnées géographiques, la latitude pour en déduire la parallaxe de la planète et la longitude de manière à synchroniser les observations.
Par cette méthode, Halley espérait déterminer la parallaxe solaire à 1/500 près si l’observation des contacts était faite à deux secondes de temps près.
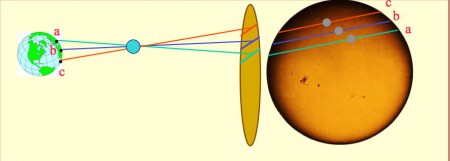
L’astronome français Joseph-Nicolas Delisle (1688-1768) propose, dès 1722, une autre méthode portant sur l’observation d’une phase unique du passage (premier ou dernier contact intérieur); cette méthode permet d’augmenter la liste des lieux d’observation possibles en y ajoutant tous les lieux où une seule phase est visible. Mais elle demande une très bonne connaissance des longitudes des lieux d’observation, chose difficile à obtenir en ce milieu du XVIIIe siècle.

 Comme on le voit sur ces deux photographies, la tache noire de Mercure (en haut, transit de 2006) est notablement plus petite que celle de Vénus (en bas, transit de 2004), ce qui complique la mesure précise des temps d’entrée et de sortie sur le disque solaire.
Comme on le voit sur ces deux photographies, la tache noire de Mercure (en haut, transit de 2006) est notablement plus petite que celle de Vénus (en bas, transit de 2004), ce qui complique la mesure précise des temps d’entrée et de sortie sur le disque solaire.
Les passages de Mercure au XVIIIe siècle
L’idée de Halley d’exclure les passages de Mercure pour déterminer la parallaxe solaire ne fait pas l’unanimité parmi les astronomes de l’époque. Ainsi William Whiston (qui, tout comme Halley, est un proche de Newton) édite la liste de tous les passages de Mercure et de Vénus sur une période de deux siècles, et estime que l’on a de meilleures chances d’obtenir la parallaxe solaire à l’aide des passages de Mercure qu’à l’aide des passages de Vénus, chose qu’il justifie en faisant remarquer que l’on connaît mieux l’orbite de Mercure, et que le passage de Mercure en 1753 sera plus central que le passage de Vénus en 1761.

De fait, en France, Joseph-Nicolas Delisle observe le passage de 1723, mais ne peut en déduire une valeur de la parallaxe solaire. En 1724, il se rend à Londres où il rencontre Halley, et revient en France avec les tables astronomiques des mouvements du Soleil, de la Lune et des planètes. Ces tables, construites par Halley, ne seront publiées, après correction, qu’en 1749 (sept ans après la mort de Halley). En 1725, Delisle part en Russie pour une période de quatre ans. Il y reste en réalité vingt-deux ans et ne rentre en France qu’en 1747.
Entre temps, le passage de Mercure de 1743 est également observé mais ne donne pas de résultats satisfaisants. Comme le signale Nicolas Louis de La Caille peu de temps avant de partir pour l’Afrique du Sud: « Or en 1743, le Ciel étant fort serein, […] des astronomes des plus habiles qui observèrent avec d’excellents Télescopes le contact intérieur de Mercure et du Soleil, diffèrent beaucoup entre eux ; et la différence alla à plus de 40 secondes de temps. ». On est bien loin des deux secondes de précision escomptées par Halley.

Le passage de Mercure de 1753, pour lequel Mercure passe à deux minutes du centre du Soleil, est une répétition grandeur nature du futur passage de Vénus. Ce passage relativement long, presque huit heures, est censé permettre une mesure plus précise. À l’automne 1752, Delisle envisage des observations depuis le Québec, l’île de Saint-Domingue et Cayenne à l’Ouest, et à l’Est, aux Indes orientales (Pondichéry), Chandernagor, Macao et Pékin. Les prédictions et la “mappemonde” représentant la projection géographique du passage sont largement diffusées auprès des astronomes de tous les pays.

Malgré l’observation du passage par des observateurs confirmés, les résultats sont de nouveau décevants et le jeune astronome français Guillaume Le Gentil conclut, fin 1753, qu’en raison de la vitesse de la planète, il est impossible de mesurer l’instant des contacts avec une précision meilleure que deux secondes de temps. Néanmoins, l’observation du passage permet de confirmer les écarts importants qui existent entre les meilleures tables planétaires de l’époque. Ainsi, le calcul du passage avec les tables de la Hire donne un dernier contact 8 heures plus tôt que le calcul fait avec les tables de Halley. Le calcul fait avec les tables de Delisle donne ce même contact dix-sept minutes plus tard… Ces écarts incitent donc Le Gentil à améliorer les tables de Vénus avant le passage de 1761.
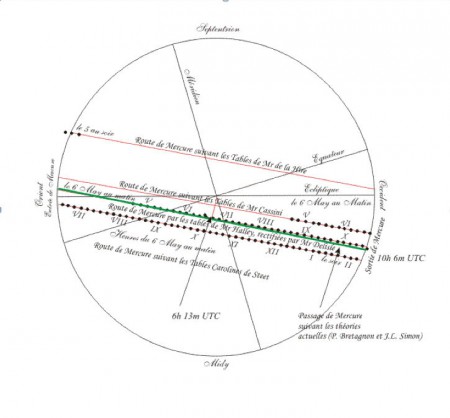
Le dessin ci-dessous, publié par Delisle, donne les différents trajets possibles de Mercure en fonction des théories utilisées. En vert a été ajouté le tracé du passage de Mercure calculé à l’aide des théories actuelles.
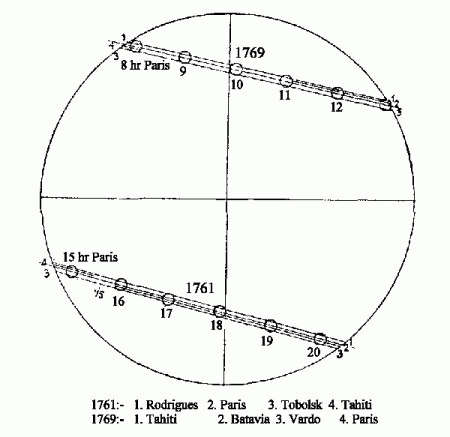
La fabuleuse histoire des expéditions de 1761 et de 1769 pour observer les passages de Vénus en divers lieux de la planète et en déduire la parallaxe solaire par la méthode de Halley est bien connue. Je lui ai même consacrée mon premier roman, Le rendez-vous de Vénus, publié en 1998.
 |  |
Pour revenir aux transits de la plus modeste Mercure, je termine en mentionnant celui du 7 novembre 1914, parfaitement observable en Europe alors plongée en pleine Guerre Mondiale.

L’événement a inspiré le peintre et sculpteur italien Giacomo Balla, rallié au mouvement futuriste :

Quant au transit du 9 mai 2016 qui fait l’actualité, je renvoie mes lecteurs qui veulent savoir comment l’observer au tout récent billet de Jean-Baptiste Feldman sur Futura Sciences.
Rêvons pour conclure à des transits simultanés de Mercure et de Vénus devant le Soleil. C’est possible, mais on se doute qu’ils sont extrêmement rares : les prochains se produiront en 69 163 et en 224 508. Patience, jusque-là…

Très intéressant. On voit comment les astronomes tirent parti de leur observations pour améliorer leur connaissances. C’est fascinant d’arriver par le calcul à prévoir ces événements cosmiques. Malheureusement ceux-ci sont rares à l’échelle d’une vie humaine. C’est assez émouvant de voir que Halley à laisser des instructions à ses confrères du futur pour leur permettre de réaliser les bonnes mesures.