Suite du billet précédent Interstellar : un trou noir à Hollywwod (1)

La plaque du foyer noir,
de réels soleils des grèves :
ah ! puits des magies.
Arthur Rimbaud, Illuminations

Depuis sa diffusion  le 5 novembre dernier sur les écrans du monde entier, le film  Interstellar de Christopher Nolan s’est imposé comme le blockbuster de l’année,  suscitant des centaines de débats et dicussions passionnées sur la toile,  alimentant des dizaines de blogs (la majorité anglo-saxons) qui ont, soit encensé, soit critiqué les exactitudes ou inexactitudes scientifiques  du film, la vraisemblance du scénario, etc.  Je rappelle que le conseiller scientique du film est mon collègue chercheur, le célèbre physicien américain Kip Thorne; avec son équipe de la compagnie  privée  Double Negative spécialisée dans les effets visuels, ils ont notamment concocté l’image du disque d’accrétion illuminant le trou noir “Gargantua”, censée être la plus précise jamais montrée, et qui a fait le tour du monde.

Pour accompagner la promotion du film, Kip Thorne a lui-même publié un livre de vulgarisation intitulé “The Science of Interstellar“, dans lequel il explique comment il a tenté de respecter le mieux qu’il pouvait l’exactitude scientifique, malgré les exigences parfois étranges du réalisateur, s’assurant en particulier que les despriptions visuelles des trous noirs et des effets relativistes associés soient les plus réalistes possibles.

Puisque, comme déjà rappelé dans le billet précédent, j’ai été en 1979 le premier chercheur au monde à effectuer des simulations numériques et à publier une image réaliste simulée d’un trou noir entouré d’un disque d’accrétion, dans les billets qui suivent je reviendrai aux bases de la visualisation des trous noirs, dans une visée non point critique mais pédagogique. Une bonne partie est adaptée d’un chapitre d’un de mes livres publié en français en 2006 chez Fayard, Le destin de l’univers, et repris en livre de poche en 2010 chez Folio/Gallimard.

 Peut-on photographier un trou noir ?

 En physique, on aime visualiser concrètement l’objet que l’on étudie. Hélas, il semble impossible de filmer ou de photographier un trou noir, puisqu’il ne laisse échapper aucune matière, aucun rayon lumineux. Le trou noir est a priori parfaitement invisible. Cependant, il n’est pas nécessaire qu’un objet émette de la lumière pour qu’on puisse le distinguer ; on peut aussi l’éclairer, de manière à ce qu’il renvoie la lumière qu’il reçoit. Dans le domaine astronomique, les planètes, dont le cœur n’est pas alimenté en énergie thermonucléaire, resteraient invisibles si leur surface ne réfléchissait pas la lumière du Soleil.

Ce qui est vrai pour une planète l’est aussi pour un trou noir. On ne verra certainement rien en l’absence de toute source d’éclairage, mais un trou noir convenablement éclairé est capable de renvoyer une image grâce aux trajets particuliers suivis par la lumière émise dans son voisinage.

Ainsi photographiés sous les feux des projecteurs, les trous noirs, qui ne sont pas des trous mais des régions de l’espace-temps aux propriétés physiques spécifiques, ne sont pas non plus vraiment noirs.

Une question d’éclairage

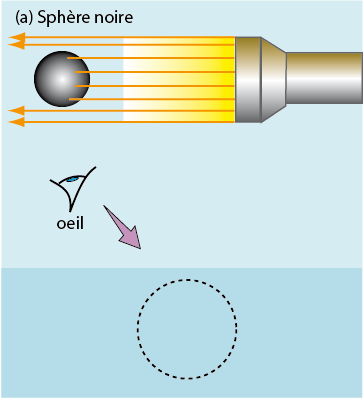
Chaque corps naturel absorbe et réfléchit à sa façon le rayonnement électromagnétique. L’expérience de pensée illustrée sur les 4 figures qui suivent  consiste à éclairer d’un faisceau de rayons parallèles diverses espèces de corps sphériques, et à observer la lumière réfléchie dans une direction perpendiculaire. L’aspect de l’image reçue révèle la façon dont les corps, selon leur nature, réagissent aux ondes électromagnétiques.

Dans le cas d’un corps parfaitement noir, comme une sphère peinte (a), tous les rayons lumineux sont absorbés. Puisque aucun rayon n’est réfléchi, l’observateur ne voit rien de la sphère éclairée.

Dans le cas d’une surface mate, 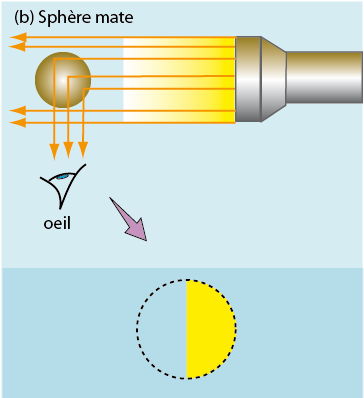comme la Lune ou les planètes (b), la lumière est réfléchie avec la même intensité dans toutes les directions. Par conséquent, en chaque point de la surface, un rayon lumineux et un seul est dévié d’exactement 90 degrés en direction de l’observateur : celui-ci voit l’image familière de la demi-lune.

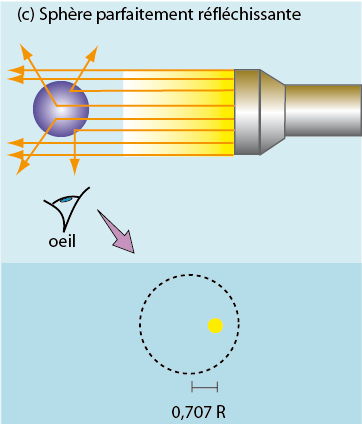Sur une sphère métallique parfaitement réfléchissante (c), un seul point de la surface dévie un rayon incident de 90 degrés et le renvoie en direction de l’observateur : l’image de la sphère se réduit donc à un point lumineux unique, situé à √2/2 ≈ 0,707 fois le rayon de la sphère.

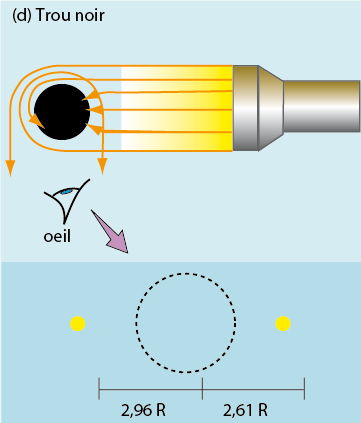Par rapport aux corps précédents, le trou noir (d) n’a pas de surface tangible sur laquelle les rayons puissent frapper et se réfléchir. C’est son champ gravitationnel qui dévie les rayons lumineux. La sphère d’influence du trou noir ne se réduit pas à sa seule surface – l’horizon des événements – mais s’étend jusqu’à l’infini. En conséquence, les rayons lumineux ne sont plus des lignes droites brisées au point d’impact avec la surface, mais des lignes d’autant plus courbées qu’elles passent près de la surface. L’image du trou noir est donc constituée d’une suite infinie de points lumineux. L’un d’entre eux, situé à gauche à 2,96 fois le rayon du trou noir, appelé « image primaire », est formé par l’unique rayon lumineux dévié de 90 degrés. L’autre, à droite, ou image secondaire, situé à 2,61 fois le rayon du trou noir, provient du rayon lumineux qui a tourné d’un demi-tour supplémentaire, c’est-à-dire de 270 degrés. Le calcul complet des trajectoires des rayons lumineux dans l’espace-temps de Schwarzschild qui entoure le trou noir montre qu’il existe en théorie une infinité de points lumineux, correspondant aux rayons déviés de tous les demi-tours supplémentaires ; mais en pratique, ces images d’ordre supérieur sont tellement proches des images primaire et secondaire qu’elles ne peuvent pas être résolues.

On s’aperçoit ainsi que, parmi les diverses espèces de corps qui ne sont pas brillants par eux-mêmes, le trou noir n’est pas le plus sombre. Il renvoie même mieux l’éclairage qu’une sphère peinte en noir et qu’une sphère parfaitement réfléchissante !

 Le trou noir en gloire

Une variante de l’expérience précédente consiste à éclairer le trou noir par des rayons parallèles et à observer la lumière réfléchie non plus à angle droit, mais dans la même direction. Ce « retour de lumière » est montré sur la figure ci-dessous. L’image du trou noir proprement dit est agrandie, son diamètre apparent étant 3√3/2 ≈ 2,6 fois plus grand que son diamètre réel. Cela vient du fait qu’une bonne partie du faisceau incident est capturée par le trou noir : non seulement les rayons interceptant directement l’horizon des événements, mais également ceux passant à moins de 5,2 M du centre (le rayon propre du trou noir étant égal à 2 M). D’autre part, le disque noir est entouré d’une auréole lumineuse constituée d’anneaux concentriques. L’anneau extérieur, à 5,34 M du centre, est dessiné par les rayons ayant accompli un demi-tour, les anneaux plus internes par les rayons ayant accompli des demi-tours supplémentaires. L’image évoque l’effet de gloire bien connu en optique traditionnelle : lorsque la lumière solaire est diffusée par les innombrables gouttelettes d’eau du brouillard, il est parfois possible d’apercevoir en réflexion l’ombre de sa propre tête, entourée d’anneaux brillants centrés sur la ligne de visée.

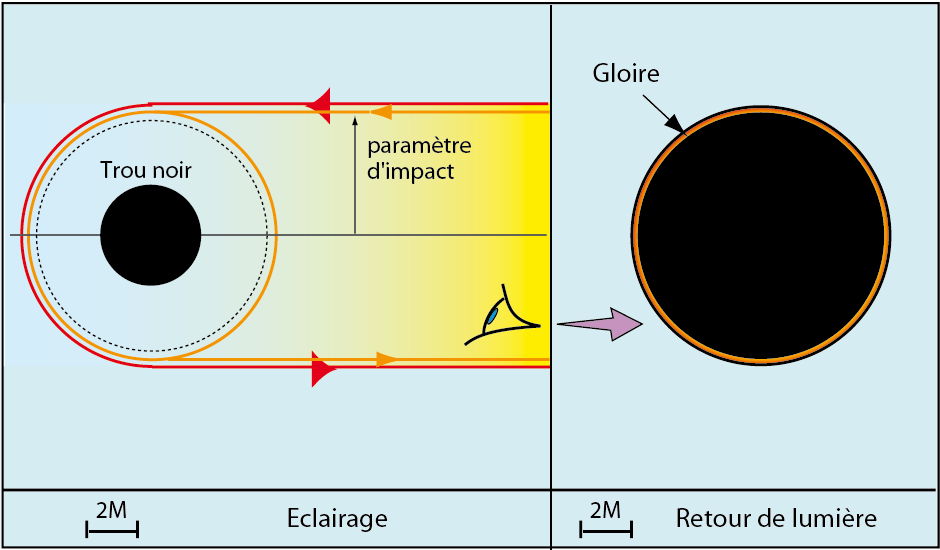
Dans le cas du trou noir glorieux, seul l’anneau extérieur serait visible, la résolution n’étant pas suffisante pour distinguer les retours de lumière d’ordre plus élevé.

En 2002, les chercheurs américains  David Holz et John Wheeler ont émis l’hypothèse que l’anneau primaire serait détectable dans le cas d’un trou noir isolé de masse stellaire situé à la frontière de notre système solaire et renvoyant à 180° les rayons de notre propre étoile, le Soleil.  John Wheeler, toujours très imaginatif dans l’appellation des phénomènes (on lui doit les termes mêmes de trou noir et trou de ver), a titré son article « Retro-MACHO : pi dans le ciel », faisant à la fois allusion au fait que les trous noirs isolés appartiendraient à la classe des MACHOS (Massive Astrophysical Compact Halo Objects), candidats pour la matière noire baryonique, et à leur observabilité grâce à la déviation de la lumière selon l’angle « magique » pi.

Durant toute sa longue vie, John Wheeler a aimé avancer des idées non conventionnelles, qui, pour la plupart d’ailleurs, se sont révélées très fructueuses. Cette dernière proposition a toutefois peu de chances de se concrétiser un jour. Le calcul du retour de lumière implique en effet un trou noir de 10 M_S situé à moins de 3 années-lumière, la magnitude du halo ne dépassant pas 32 dans le cas le plus favorable (soit une magnitude 100 fois moindre que celle du plus faible objet jusqu’alors détecté par les plus puissants télescopes). Par ailleurs, on estime que la densité moyenne de trous noirs de masse stellaire dans notre région de la Galaxie est de l’ordre de 0,00001 par année-lumière cube. Il serait donc extraordinairement improbable qu’un trou noir stellaire se trouve aussi près de nous! Admettons cependant l’hypothèse, à savoir un trou noir de 1 M_S situé à seulement à 1,5 année-lumière de nous. Le calcul indique qu’il ferait alors office de « retro-macho » de magnitude 43, soit une luminosité 100 000 fois plus faible que celle du plus faible objet jamais détecté…

Optique dans l’espace-temps courbe

Quelle est la justification de cette surprenante « optique géométrique » du trou noir ? Cette optique considère la courbure des rayons lumineux comme une caractéristique fondamentale de la théorie de la relativité générale, selon laquelle la propagation des rayons lumineux dépend des champs de gravitation. L’Univers se décrit comme un espace-temps à quatre dimensions, sorte de tissu souple et élastique déformé par la gravitation, c’est-à-dire par les corps massifs qu’il contient. Formant la trame de ce tissu, les trajets de la lumière sont comme des fils jetés sur les abîmes. Tout comme la matière,l’énergie engendre un champ gravitationnel (puisqu’elles sont équivalentes, liées par la formule E = mc²) ; réciproquement, matière et énergie subissent les effets de la gravitation. Notamment, les particules sans masse mais en mouvement, tels les corpuscules de lumière nommés photons, possèdent une énergie : leurs trajectoires sont donc modifiées par la gravitation. Ainsi, les rayons lumineux suivent des trajectoires d’autant plus incurvées que le champ gravitationnel qu’ils traversent est intense. Dans une excellente approximation, qui revient à négliger l’influence du champ gravitationnel propre du photon devant celui du trou noir, la lumière émise par chaque photon suit une trajectoire géodésique, c’est-à-dire la ligne de plus court trajet entre deux points. Les géodésiques sont des lignes droites dans l’espace-temps plat et elles épousent la forme d’un espace-temps courbe.

Le champ gravitationnel d’un trou noir courbe fortement l’espace-temps dans son voisinage. À partir d’une certaine distance de son centre, qui définit l’horizon des événements, aucune particule (massive ou non) ne peut échapper à son emprise. À l’extérieur de l’horizon des événements (qui est la surface du trou noir proprement dite), les rayons lumineux peuvent s’échapper, mais l’importante courbure de l’espace-temps modifie considérablement leur trajectoire.

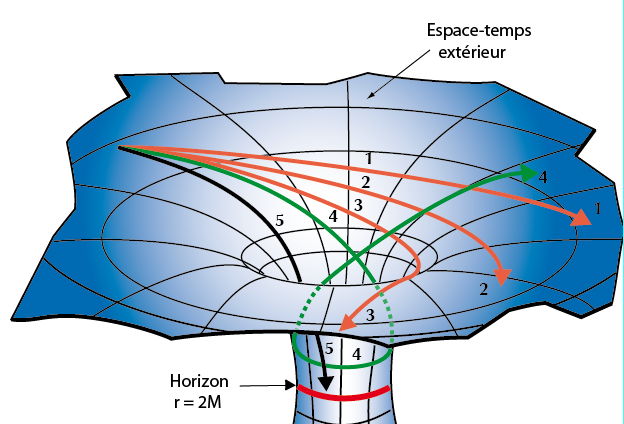
On peut faire confiance aux équations de la relativité générale pour calculer la propagation des rayons lumineux au voisinage des trous noirs. Le calcul nécessite une analyse mathématique préalable, suivie d’une intégration numérique par l’ordinateur. C’est par cette méthode que l’on peut obtenir les images d’un trou noir éclairé par des sources de n’importe quelle nature et distribuées de n’importe quelle façon.

C’est ce que nous verrons dans le billet suivant