Suite du billet précédent La physique étrange d’Insterstellar (2/6)

En novembre 2014, le film de science-fiction Interstellar (réalisation Christopher Nolan, Warner Bros Pictures, 169 minutes, 2014) sortait sur nos écrans. Véritable “blockbuster” hollywoodien, il a suscité un énorme battage médiatique, comme en témoignent les innombrables forums de discussion et articles de presse ayant fleuri au cours des jours, semaines et mois qui ont suivi.  A la demande de la revue de langue anglaise Inference : International Review of Science, j’ai par la suite fait un travail d’analyse scientifique beaucoup plus développé et approfondi, publié au printemps 2015. Je vous en livre la traduction française, découpée en 6 billets. Celui-ci est le troisième.

Visualisation du disque d’accrétion

Interstellar est le premier film long métrage d’Hollywood qui tente de représenter correctement un trou noir tel qu’il apparaîtrait à un observateur proche de lui. L’image sans doute la plus captivante du film est le spectacle de Gargantua et de son disque d’accrétion se déployant tout autour et devant lui.

Un trou noir engendre des déformations extrêmes de l’espace-temps. Il crée aussi les déviations de rayons lumineux les plus fortes possibles. Cela engendre de spectaculaires illusions d’optique de type « mirage gravitationnel ». Pour les représenter, la compagnie en charge des effets spéciaux du film, Double Negative, a développé en collaboration avec Kip Thorne un logiciel capable d’intégrer les équations de propagation de la lumière dans l’espace-temps courbe du trou noir[1]. Les équations produites pour le film ont permis de décrire le mirage gravitationnel produit sur les étoiles d’arrière-plan, tel qu’il serait vu par une caméra proche de l’horizon des événements[2].

Compte tenu des immenses distances mises en jeu dans l’observation astronomique des trous noirs et de la trop faible résolution de nos télescopes actuels, aucune image détaillée de disque d’accrétion n’a encore été obtenue[3]. Mais en 1979, j’ai été le premier à simuler (en noir et blanc) l’aspect d’un disque d’accrétion mince gravitationnellement déformé par un trou noir sphérique, tel qu’il serait vu par un observateur lointain ou saisi par une plaque photographique[4].

Dans l’espace euclidien, la courbure est faible. C’est le cas dans le système solaire quand on observe les anneaux de la planète Saturne selon un angle légèrement au-dessus de leur plan. Une partie des anneaux reste cachée derrière la planète, mais on peut reconstituer aisément leur forme elliptique. Autour d’un trou noir, les déformations optiques dues à la courbure de l’espace-temps donnent un visuel très différent. En premier lieu, on peut voir le dessus du disque d’accrétion dans sa totalité, quelque soit l’angle de vue. La partie arrière du disque n’est pas cachée par la silhouette du trou noir, car son image est « relevée » par la courbure et devient visible à tout observateur distant. De façon plus étonnante, on peut aussi voir le « dessous » du disque d’accrétion : les rayons lumineux qui normalement se propagent dans la direction opposée à celle de l’observateur remontent vers le haut et fournissent une image très déformée, dite « secondaire », de l’autre face du disque[5].

[Pour des images et des explications plus détaillées, voir mon billet de novembre  2014  Interstellar : un trou noir à Hollywood].

C’est pourquoi, lorsque j’ai vu pour la première (et unique) fois Interstellar, je n’ai pas été surpris par l’image du disque d’accrétion s’étendant tout autour et devant la noire silhouette de Gargantua. Bien que l’équipe réalisatrice de ces images puisse légitimement être fière de son travail, je suis resté perplexe devant les communiqués de presse prétendant (promotion à l’américaine oblige !) qu’il s’agissait de la première et plus réaliste image jamais faite d’un disque d’accrétion autour d’un trou noir. En effet, un certain nombre d’effets optiques avaient de toute évidence été omis.

Dans ma simulation de 1979, j’avais aussi tenu compte des propriétés physiques du disque gazeux: sa rotation, sa température et son émissivité. Pour un disque mince, l’intensité du rayonnement émis en un point donné du disque dépend de sa distance au trou noir. Par conséquent, la luminosité du disque ne peut pas être uniforme, contrairement à ce qui est montré dans Interstellar. La brillance maximum provient des régions les plus proches de l’horizon des événements, là où le disque est le plus chaud.
Cependant, la luminosité apparente du disque est très différente de sa luminosité intrinsèque. Le rayonnement reçu est décalé en fréquence et en intensité. Il y a deux types de décalages : primo, l’effet Einstein, par lequel le champ gravitationnel abaisse la fréquence et diminue l’intensité; secundo, l’effet Doppler, par lequel le déplacement de la source par rapport à l’observateur produit une amplification quand la source se rapproche et une atténuation quand elle s’éloigne. Dans le cas du trou noir, c’est la rotation rapide du disque d’accrétion qui induit l’effet Doppler. Les régions du disque les plus proches du trou noir tournent à une vitesse proche de celle de la lumière, de sorte que le décalage Doppler est considérable et modifie drastiquement l’image reçue par un observateur lointain. La rotation du disque est supposée telle que la matière s’éloigne de l’observateur dans la partie disons droite de l’image, et se rapproche dans la partie gauche. Quand la matière s’éloigne, l’affaiblissement Doppler s’ajoute à l’affaiblissement gravitationnel, induisant une très forte atténuation de la luminosité dans la partie droite de l’image. Au contraire, dans la partie gauche, les deux effets se contrarient, de sorte que l’image apparente garde plus ou moins sa brillance intrinsèque. Quoi qu’il en soit, une image réaliste doit forcément exhiber une forte asymétrie de la luminosité du disque, avec un côté nettement plus brillant que l’autre[6].

Ces effets affectent aussi les couleurs, lesquelles ne pouvaient être vues dans mon image noir et blanc (en fait bolométrique) de 1979. Mais, inspirées par mon travail, des visualisations toujours plus sophistiquées ont vu le jour dans les années qui ont suivi. Jun Fukue et Takushi Yokoyama ont ajouté des couleurs au disque[7], S. U. Viergutz a introduit la rotation du trou noir et produit des images colorées[8]. Le travail de Jean-Alain Marck[9] a ensuite posé les bases d’une visualisation animée, dans laquelle la caméra se déplace de part et d’autre du disque d’accrétion, et inclut des images multiples d’ordre élevé[10]. Un logiciel sophistiqué de « tracé de rayons » et des modèles de flots d’accrétion a récemment été développée, fournissant des simulations 3D de structures d’accrétion et leurs images associées[11].

Kip Thorne n’ignorait évidemment pas ces effets. Ce sont en fait les auteurs du film qui ont décidé d’omettre les décalages Einstein et Doppler ainsi que les propriétés physiques du disque, montrant ainsi un disque d’accrétion de forme correcte mais de brillance inexacte. Dans un courriel qu’il m’a spontanément adressé en novembre 2014, Thorne m’a expliqué que ces simplifications avaient été décidées à la demande du réalisateur et du producteur, afin d’éviter que les spectateurs soient trop déroutés. Et pour simplifier encore davantage, ils ont aussi choisi d’appliquer les calculs de Thorne à un trou noir plus petit que Gargantua et tournant considérablement moins vite. Sinon, selon eux, les effets visuels seraient devenus extrêmement bizarres, voire incompréhensibles y compris pour des physiciens… De façon à exploiter à fond le logiciel de tracé de rayons développé pour Interstellar, Thorne et ses collaborateurs de Double Negative ont publié ultérieurement un article technique incluant toutes les corrections[12].

Forces de marée et vagues géantes

Après l’atterrissage sur Miller, monde entièrement recouvert d’un océan peu profond, les astronautes d’Interstellar sont confrontés à de gigantesques vagues venant périodiquement balayer la planète. Deux éléments de cette scène fournissent matière à objection : une planète peut-elle orbiter si près d’un trou noir sans être déchirée par les forces de marée, et les vagues de hauteur kilométriques montrées dans le film sont-elles physiquement réalistes[13]?

Lorsqu’un objet, planète ou étoile, orbite autour d’un trou noir, l’attraction gravitationnelle exercée par le trou s’exerce plus fortement sur la partie de l’astre la plus proche du trou que sur la partie opposée. La force de marée est la différence entre ces forces gravitationnelles. Si l’astre se meut sur une orbite circulaire à distance raisonnable du trou noir, les forces de marée restent faibles, l’astre peut ajuster sa configuration d’équilibre interne aux forces externes, et adopte une forme légèrement allongée en direction du trou noir. Toutefois, si l’astre se déplace sur une orbite excentrique, à mesure que sa distance r au trou noir diminue, les forces de marée croissent rapidement comme r^-3. Finalement, une limite est atteinte lorsque les forces externes deviennent plus grandes que les forces de liaison de l’astre. Ce dernier n’a plus le temps d’ajuster sa configuration d’équilibre et commence à se disloquer.

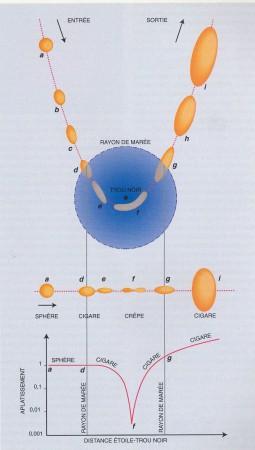
Dans les années 1980 j’ai beaucoup travaillé sur le processus par lequel des étoiles entières pouvaient être brisées par des trous noirs géants[14]. Dans les cas extrêmes, quand une étoile en orbite parabolique frôle l’horizon des événements du trou noir sans être avalée, j’ai prédit l’occurrence de “crêpes stellaires flambées,” libérant de grandes quantités d’énergie radiative[15]. Depuis lors les télescopes ont capturé de telles scènes cosmiques. Mais ces événements ne peuvent se produire que lorsque l’étoile pénètre à l’intérieur d’une certaine distance critique au trou noir, appelée limite de Roche[16].

Il s’avère qu’Interstellar est (marginalement) correct sur ce point. En effet, la limite de Roche dépend de la masse du trou noir et de la densité moyenne de l’astre extérieur: R_R ~ (M/ρ*)^1/3, où M est la masse du trou noir et ρ* la densité de l’astre. Appliquant cette formule à Gargantua (M = 10⁸ masses solaires) et à une planète aqueuse (ρ* ~1 g/cm³), on obtient R_R ~ 10¹³ cm. Le rayon gravitationnel de Gargantua, GM/c², est aussi de l’ordre de 10¹³ cm. Le monde Miller doit donc subir de puissantes forces de marée, mais pas suffisantes pour le détruire[17].

La cause des grandes vagues de marée balayant la planète ne sont pas expliquées, mais on peut supposer qu’elles sont dues à la proximité de Gargantua. Comme on peut le voir, la longueur d’onde des vagues de marée est beaucoup plus grande que la profondeur de l’océan. Ce scénario peut être décrit par les équations de Navier–Stokes en approximation « eau peu profonde ». Il s’agit d’équations aux dérivées partielles, non linéaires et couplées, dont les solutions dépendent de la gravité de surface de la planète, de sa période de rotation, des forces de viscosité, et ainsi de suite. On nous dit que l’accélération de la pesanteur sur Miller est 130% celle de la Terre, soit g = 9.81 × 1.30 = 12.75m/s². Les autres paramètres dépendent de la structure interne de la planète, ainsi que de complexes effets externes dus au champ gravitationnel du trou noir en rotation. Les informations fournies ne permettent pas de résoudre numériquement le système d’équations.

Je suspecte cependant le film d’être incohérent sur ce point. Une vague de marée est un bourrelet aqueux fixe dans l’espace, toujours orienté dans la même configuration. Les astronautes sur Miller passent de part et d’autre du bourrelet, observant une vague s’approcher, passer puis s’éloigner : marée haute, marée basse. Les vagues surgissent à peu près chaque heure. Comme il y a deux marées hautes par rotation, la planète tourne en deux heures. Avec des marées aussi énormes, en théorie la planète devrait avoir synchronisé sa période de rotation propre avec sa période de révolution autour de Gargantua, autrement dit présenter toujours la même face au trou noir (comme la Lune face à la Terre). L’échelle de temps typique pour un tel « verrouillage de marée » entre un trou noir de 10⁸ masses solaires et une planète dont la gravité de surface est 13m/s² n’est que de 1 milliseconde. Une fois verrouillée au trou noir, la planète tournerait sur elle-même une fois par révolution orbitale, et à sa surface le bourrelet resterait toujours dirigé vers le trou noir.

La suite est à lire ici : La physique étrange d’Interstellar (4/6) : Dilatation temporelle et processus de Penrose

REFERENCES

[1] Adam Rogers, “How Building a Black Hole for Interstellar Led to an Amazing Scientific Discovery,” Wired, October 22, 2014.

[2] Les meilleures simulations disponibles montrant les effets de lentille gravitationnelle d’un trou noir sur un fond étoilé sont celles d’Alain Riazuelo [http://www2.iap.fr/users/riazuelo/interstellar/index.php]. Ce chercheur, l’un des meilleurs spécialistes du sujet, a calculé la silhouette de trous noirs en rotation très rapide, comme Gargantua, devant un arrière-plan céleste constellé de plusieurs milliers d’étoiles.

[3] Le projet d’obtenir des images télescopiques de disques d’accrétion en utilisant l’interférométrie à grande base est tout proche d’aboutir grâce à la collaboration internationale [http://eventhorizontelescope.org/].

[4] Jean-Pierre Luminet, “Image of a Spherical Black Hole with Thin Accretion Disk,” Astronomy and Astrophysics 75 (1979): 228–35.

[5] En théorie, il y a une image tertiaire donnant une vue encore plus distordue du dessus du disque, après que les rayons lumineux aient effectué trois-quarts de tour, puis une image du dessous d’ordre quatre encore plus écrasée, et ainsi de suite jusqu’à l’infini.

[6] Pour décrire l’image finale que j’avais obtenue, nulle légende ne convient mieux que ces vers du poète Gérard de Nerval datant de 1854:

En cherchant l’œil de Dieu je n’ai vu qu’un orbite
Vaste, noir et sans fond, d’où la nuit qui l’habite
Rayonne sur le monde et s’épaissit toujours
Un arc-en-ciel étrange entoure ce puits sombre,
Seuil de l’ancien chaos dont le néant est l’ombre,
Spirale engloutissant les Mondes et les Jours !

Gérard de Nerval, “Le Christ aux Oliviers” dans Les chimères, poésie et théâtre (Paris: Le Divan, 1928): 39.

[7] Jun Fukue and Takushi Yokoyama, “Color Photographs of an Accretion Disk around a Black Hole,” Publications of the Astronomical Society of Japan 40 (1988): 15–24.

[8] S. U. Viergutz, “Image Generation in Kerr Geometry. I. Analytical Investigations on the Stationary Emitter-Observer Problem,” Astronomy and Astrophysics 272 (1993): 355–77.

[9] Jean-Alain Marck, “Short-Cut Method of Solution of Geodesic Equations for Schwarzschild Black Hole,” Classical and Quantum Gravity 13, no. 3 (1996) 393–402. De façon plus accessible, voir aussi Jean-Alain Marck et Jean-Pierre Luminet, “Plongeon dans un trou noir,” Pour la Science Hors-Série “Les trous noirs” (Juillet 1997) 50–56.

[10] Jean-Alain Marck, “Color Animation of a Black Hole with Accretion Disk.” Video YouTube. Une version filmique est parue pour la première fois dans le documentaire Infiniment Courbe par Laure Delesalle, Marc Lachièze-Rey et Jean-Pierre Luminet (France: CNRS/Arte, 1994).

[11] Pour des simulations relatives au trou noir galactique Sagittarius A*, voir Chi-Kwan Chan et al., “The Power of Imaging: Constraining the Plasma Properties of GRMHD Simulations Using EHT Observations of SgrA*,” Astrophysical Journal 799, no. 1 (2014).

[12] Oliver James et al., “Gravitational Lensing by Spinning Black Holes in Astrophysics and in the Movie Interstellar,” Classical and Quantum Gravity 32 no. 6 (2014): 1–41.

[13] Phil Plait, “Interstellar Science,” Slate, November 6, 2014.

[14] Jean-Pierre Luminet and Brandon Carter, “Dynamics of an Affine Star Model in a Black Hole Tidal Field,” The Astrophysical Journal Supplement Series 61 (1986): 219–48.

[15] Brandon Carter and Jean-Pierre Luminet, “Pancake Detonation of Stars by Black Holes in Galactic Nuclei,” Nature 296 (1982): 211–14.

[16] La limite de Roche est nommée d’après Édouard Roche, mathématicien et astronome français qui a étudié le problème des forces de marée dans le contexte des planètes et de leurs satellites. Roche l’avait calculée en 1847.

[17] Pour les trous noirs plus gros que 10⁸ masses solaires, dont on suspecte la présence au centre des quasars, la limite de Roche devient significativement plus petite que le rayon gravitationnel. En ce cas, les planètes ou les étoiles ne sont brisées par les forces de marée qu’après avoir pénétré dans le trou noir, ce qui ne laisse aucun effet astronomiquement observable.