Dans l’île grecque de Samos, on peut visiter un tunnel qui, selon Hérodote, fut creusé au VIe siècle avant notre ère, simultanément par ses deux extrémités … et l’erreur au point de rencontre ne fut que de 60 centimètres, comme le tracé du tunnel l’atteste toujours. On ne sait pas comment son architecte, Eupalinos, en fit les plans, mais on sait qu’ils ne doivent rien au hasard. La plupart des historiens qui se sont penchés sur la question en on déduit qu’Eupalinos avait anticipé les instruments et les mathématiques inventés plusieurs siècles après sa mort. Est-ce vraisemblable ? Pourquoi les aurait-on oubliés ensuite ? De plus, pourquoi faire des hypothèses inutiles ? Il est plus raisonnable d’essayer d’imaginer des méthodes compatibles avec les mathématiques et les instruments connus de l’époque.
Un aqueduc extérieur imaginaire …

De la source captée jusqu’à l’entrée du tunnel, l’eau suit des conduites extérieures, quoique enterrées. On peut imaginer que, dans un premier temps, l’aqueduc allait ainsi jusqu’à la sortie du tunnel en suivant grossièrement les lignes de niveaux du terrain. La topographie le permet comme le montre la carte du lieu.
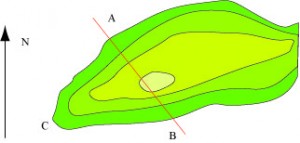
…qui aide à trouver la sortie
Cette hypothèse est difficile à soutenir car aucun vestige d’un tel ouvrage ne nous est parvenu. De plus, le tunnel est quasiment horizontal, seul le canal qui le longe a une déclivité de six mètres sur un peu plus d’un kilomètre. Cette hypothèse d’un aqueduc extérieur donne cependant une première approche du problème, naturelle pour un constructeur d’aqueduc. Pour déterminer l’entrée et la sortie, il s’agit de se déplacer à l’horizontale au flanc de la montagne, pour rejoindre un point duquel l’aqueduc peut continuer. Des preuves archéologiques montrent que les Samiens disposaient d’instruments pour déterminer l’horizontale. Le principe en est simple. Il s’agissait de longues gouttières en terre cuite dans lesquelles on versait de l’eau. L’horizontale était obtenue quand l’eau ne s’écoulait pas. De même, ils utilisaient des fils à plomb, ce qui permettait de déterminer la verticale. On peut imaginer suivre l’horizontale ainsi en plantant des pieux dont les sommets restent au même niveau. Si le niveau mesure 2 mètres de long, et que l’incertitude est inférieure à 1 millimètre pour chaque pieu, nous obtenons une incertitude totale de 1,10 mètres. L’erreur effective à la jonction des deux branches du tunnel étant de 60 centimètres, l’utilisation de cette méthode est vraisemblable. Cependant, elle exige de planter 1100 pieux. On peut la simplifier de ce point de vue en utilisant des visées oculaires permettant d’espacer les pieux.
Pour cela, on plante deux pieux à 10 mètres l’un de l’autre, dont les sommets sont à l’horizontale et on les aligne avec un pieu à cent mètres environ, tenu par un assistant. Ceci permet de passer à un total d’une cinquantaine de pieux (deux tous les 100 mètres environ).

L’œil humain a une capacité de résolution de 0,5 minute environ (1 / 120 degré). Avec un viseur, sur cent mètres, nous pouvons espérer une incertitude inférieure à 2 centimètres. Sur une distance de 2 200 mètres, cela donne une incertitude totale de 44 centimètres, ce qui est compatible avec l’erreur effective de 60 centimètres.
La direction de la sortie
La deuxième extrémité trouvée, comment déterminer la direction dans laquelle le tunnel doit être percé ? Une idée simple tient à la topographie du terrain. Il s’en faut de peu que l’on ne puisse voir les deux extrémités du tunnel du haut de l’Acropole. Dans ce cas, il aurait suffi d’y disposer trois pieux alignés et, par approximations successives de les aligner à des pieux plantés aux extrémités du tunnel à construire. L’opération est semblable à la précédente, sans mise à niveau.
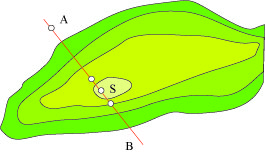
En fait, la topographie du terrain ne permet pas cette solution. On peut malgré tout l’appliquer, soit en surélevant le sommet au moyen d’une tour de dix mètres environ, soit en plantant des pieux intermédiaires. Une station supplémentaire, éventuellement légèrement surélevée, suffit pour réaliser un alignement visible de proche en proche.
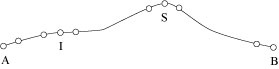
Ceci fait, les deux pieux à chaque extrémité donnent la direction à suivre. Il est facile de la conserver ensuite. Cependant, pour être sûr de se rencontrer, le mieux est d’obliquer légèrement un peu avant le milieu des travaux car, dans un plan, deux droites non parallèles se rencontrent toujours. L’une des branches du tunnel effectivement construit par Eupalinos présente des portions en zigzag montrant qu’il n’était pas certain de ses mesures et voulait éviter de manquer le deuxième tronçon qui, lui, reste rectiligne.
Le problème de la longueur du tunnel est accessoire. Même s’il est utile de la connaître pour savoir quand obliquer pour être sûr de la rencontre, il suffit d’en avoir une approximation grossière. Une fois le tunnel construit, on peut la calculer de façon plus précise et en déduire la pente à donner au canal. Finalement, sa profondeur varie de 3 à 9 mètres pour assurer un flux constant.
