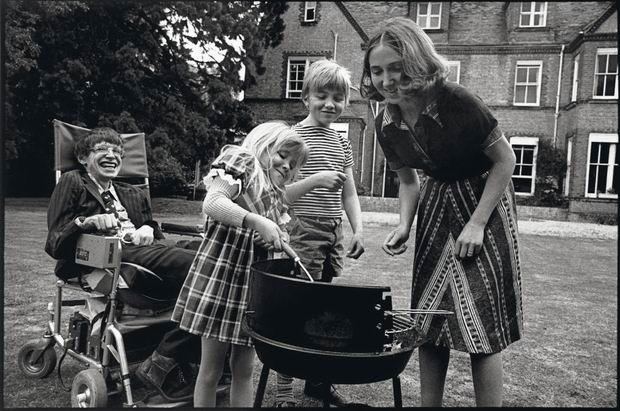Complément au billet précédent Stephen Hawking (1942-2018) : Souvenirs personnels
Les travaux de Stephen Hawking tournent essentiellement autour d’une interrogation aussi vieille que l’humanité : l’éternité du temps. Pour tenter d’y répondre de façon pertinente, le physicien britannique a utilisé l’arsenal de la physique contemporaine : la relativité générale (théorie de la gravitation), la mécanique quantique (théorie des particules élémentaires et de leurs interactions) et le problématique mariage des deux (la gravitation quantique), concentrant sa stratégie sur deux domaines clés de la recherche théorique : les trous noirs et la cosmologie.
La relativité générale prédit que les étoiles très massives s’effondrent sur elles-mêmes sans limite. Leur champ gravitationnel devient alors si grand qu’il emprisonne la matière et la lumière à l’intérieur d’un « trou noir », zone de non-retour délimitée par une surface appelée horizon des événements. À la fin des années 1960, Hawking et son mentor Roger Penrose ont démontré qu’au-delà de l’horizon, l’effondrement gravitationnel doit inévitablement se poursuivre pour atteindre un stade « singulier » où la densité devient infinie. A la question « le temps a-t-il une fin ? », la réponse est donc oui dans le cadre de la relativité générale classique : le futur s’arrête aux singularités cachées au fond des trous noirs.
Hawking s’est ensuite attaché, en collaboration avec d’autres chercheurs, à la mise en place d’une « thermodynamique des trous noirs » calquée sur les lois de la thermodynamique usuelle, autrement dit à les modéliser comme des systèmes physiques capables d’interagir avec le milieu extérieur et d’évoluer au cours du temps. Hawking a notamment démontré la loi de croissance irréversible de l’aire d’un trou noir, qui peut être mise en parallèle avec la loi de croissance de l’entropie. En outre, la gravité de surface d’un trou noir doit jouer le rôle d’une température. Un paradoxe, pointé par Jacob Bekenstein de l’Université de Princeton, surgit alors : si le trou noir possède réellement une température et une entropie, il doit être capable de rayonner de l’énergie, ce qui entre en conflit avec sa définition classique.

Le dilemme a été résolu en 1974 par Hawking (un peu par hasard a-t-il plus tard reconnu), lorsqu’il a entrepris d’étudier l’interaction d’un trou noir avec le vide quantique. Dans la conception classique du trou noir, rien ne peut sortir de l’horizon. En mécanique quantique, au contraire, en raison du principe d’incertitude, une particule a toujours une probabilité non nulle de franchir une barrière de potentiel par effet tunnel. Appliqué à la théorie des trous noirs microscopiques, le principe d’incertitude crée des sortes de « tunnels quantiques » à travers l’horizon gravitationnellement infranchissable, permettant à des particules de s’en échapper et au trou noir de s’évaporer. Cette évaporation quantique du trou noir se manifeste sous forme d’un rayonnement dont la température est bien fixée par la gravité régnant à la surface du trou noir.
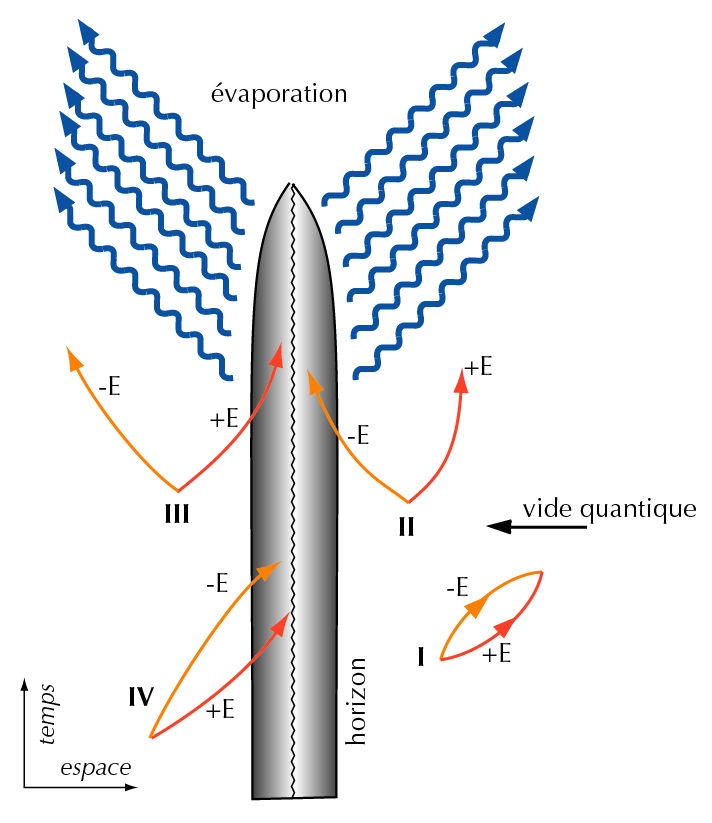
L’évaporation quantique est totalement négligeable pour les trous noirs astrophysiques de masse stellaire ou galactique, lesquels s’accroissent au cours du temps, mais Hawking a montré qu’elle deviendrait dominante pour les « mini-trous noirs » de la taille d’un proton et moins massifs qu’un milliard de tonnes, leur temps d’évaporation devenant plus court que l’âge de l’univers (quatorze milliards d’années). De tels objets auraient pu se former au cours du Big Bang, lorsque la densité d’énergie ambiante était si élevée que la moindre fluctuation aurait pu se condenser en trou noir microscopique.
Cette découverte théorique du rayonnement quantique des trous noirs – appelé depuis « rayonnement Hawking » – a permis de comprendre que les trous noirs, outre leur intérêt astrophysique, jouent le rôle d’une pierre de Rosette dans le déchiffrage des liens énigmatiques entre gravité, quantas et thermodynamique. C’est à ce titre qu’elle restera la contribution la plus importante de Hawking à la physique théorique moderne. Continuer la lecture de Stephen Hawking (1942-2018) : ses travaux