Au XIVe siècle, le philosophe franciscain Guillaume d’Ockham (1280-1349) écrivit : « il est inutile d’accomplir par un plus grand nombre de moyens ce qu’un nombre moindre de moyens suffit à produire. [ …] Quand des choses doivent rendre vraie une proposition, si deux choses suffisent à produire cet effet, il est superflu d’en mettre trois.»
…] Quand des choses doivent rendre vraie une proposition, si deux choses suffisent à produire cet effet, il est superflu d’en mettre trois.»
En d’autres termes, dans un ensemble de modèles expliquant des faits, la préférence doit être donnée à celui qui fait appel au nombre minimal d’hypothèses.
 Tout au long de l’histoire de la pensée, depuis l’Antiquité grecque jusqu’aux développements les plus récents de la physique et de la cosmologie, ce « principe de simplicité », appelé aussi « rasoir d’Ockham » car il peut servir de critère épistémologique pour trancher entre les différents modèles d’un phénomène donné, a joué un rôle-clé dans l’élaboration des modèles scientifiques, philosophiques, voire économiques (d’ailleurs, empreint d’une pensée pragmatique anglo-saxonne, il est aussi appelé « principe d’économie »).
Tout au long de l’histoire de la pensée, depuis l’Antiquité grecque jusqu’aux développements les plus récents de la physique et de la cosmologie, ce « principe de simplicité », appelé aussi « rasoir d’Ockham » car il peut servir de critère épistémologique pour trancher entre les différents modèles d’un phénomène donné, a joué un rôle-clé dans l’élaboration des modèles scientifiques, philosophiques, voire économiques (d’ailleurs, empreint d’une pensée pragmatique anglo-saxonne, il est aussi appelé « principe d’économie »).
Le critère doit cependant être appliqué avec beaucoup de prudence. Par exemple, il ne signifie pas nécessairement qu’il faille préférer l’hypothèse la plus simple. Il ne faut pas confondre simplicité et simplification, encore moins ce qui est simple avec ce qui est simpliste. J’en veux pour preuve les trois explications suivantes des mouvements célestes.

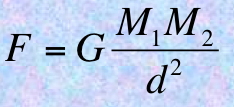

L’explication théologique est simpliste; elle ne résout rien et ne permet de faire aucun calcul, aucune prédiction. L’explication newtonienne est très efficace, mais elle fait appel à une mystérieuse action à distance instantanée, que l’on peut considérer comme une hypothèse superflue. L’explication relativiste fait l’économie de la notion de force gravitationnelle : les corps se déplacent librement selon les “droites” (géodésiques) d’une géométrie spatio-temporelle courbe. Elle fournit une représentation plus précise des mouvements observés. Certes, les équations d’Einstein sont formellement plus compliquées que la loi de Newton. Elles sont néanmoins d’une plus grande simplicité ontologique.
Accepté et correctement appliqué, le rasoir d’Ockham aurait pu hâter l’émergence de véritables révolutions scientifiques. Je donnerai deux exemples : la constitution de la matière, et la position de la Terre dans l’univers.
Dès le VIe siècle avant notre ère, les philosophes grecs débattaient sur la nature de la matière. Deux conceptions opposées s’affrontaient. D’un côté, Thalès observait la combustion d’un morceau de bois (feu, fumée, vapeur d’eau et cendres) et en concluait que la substance qui compose tout corps se réduit à quatre éléments premiers : le feu, l’air, l’eau et la terre. Plus tard, Aristote renforça la théorie des éléments en attribuant des qualités à chacun d’eux : froid, sec, chaud et humide. Il ajouta même un cinquième élément, la quintessence, censé figurer la transition entre la matière terrestre, imparfaite car corruptible, et la matière céleste, parfaite.

De l’autre côté, pour Démocrite et les philosophes de l’école atomiste, la matière était constituée d’atomes, corpuscules extrêmement petits, indivisibles (atomos signifie « insécable »), éternels et pouvant prendre, par leurs combinaisons fortuites, une infinité de formes. Dans cette conception, développée par Epicure puis Lucrèce, il n’y avait donc qu’un seul élément constitutif de la matière, l’atome, mais en nombre infini dans un espace infini, de sorte que le hasard de leurs combinaisons produisait tous les corps possibles.

Le modèle atomiste était clairement plus “économe” que celui d’Aristote. C’est toutefois la conception aristotélicienne de la matière qui s’est imposée en Occident jusqu’au XVIIe siècle, en dépit de l’argument de simplicité avancé par Ockham lui-même : “Que les matières premières de tous les corps susceptibles de génération et de corruption soient de même espèce, nous l’allons prouver. Il serait vain, en effet, d’accomplir à l’aide d’un plus grand nombre de moyens ce qui peut se faire à l’aide de moyens moins nombreux. Je dis donc qu’au sein des corps célestes aussi bien que des corps inférieurs, la matière est absolument de même espèce”.

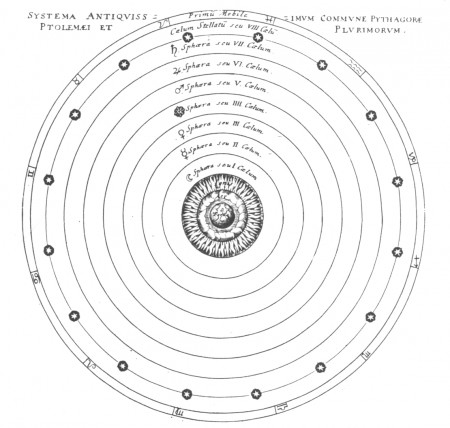
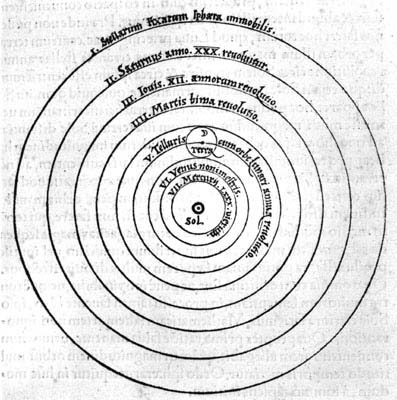
En ce qui concerne la position de la Terre dans l’univers, Aristote supposait notre planète immobile au centre de l’univers, de sorte que l’ensemble des astres, Soleil compris, devait tourner autour d’elle en 24 heures. Un astronome grec, Aristarque de Samos, démontra cependant, par d’astucieuses méthodes géométriques, que le Soleil était beaucoup plus gros que la Terre. Il était donc plus simple de supposer la petite Terre mobile autour du gros Soleil fixe. C’est pourtant le système aristotélicien, perfectionné par Ptolémée, qui s’est imposé durant de nombreux siècles. Il a fallu attendre le XIVe siècle pour que l’hypothèse de la Terre mobile réapparaisse.
Ainsi, Jean Buridan utilise le principe de simplicité d’Ockham pour déclarer : « Il est mieux de rendre compte des apparences par peu que par beaucoup de causes, si c’est possible, et de même d’en rendre compte par la voie la plus facile. Or il est plus facile de mouvoir ce qui est petit que ce qui est grand ; il est donc mieux de dire que la terre, qui est petite, se meut très rapidement et que la sphère suprême [le Soleil] est immobile, que de dire le contraire ». Dans son fameux traité Des révolutions des orbes célestes (1543), Nicolas Copernic argumente à la façon d’Ockham : « Dans ce temple magnifique, qui donc placerait cette lampe [le Soleil] en un lieu autre et meilleur que celui d’où elle peut éclairer tout en même temps ? »
Kepler et Galilée mettront la touche finale à cette révolution majeure de la pensée, qui marque la naissance de l’astronomie moderne. L’argumentation de Galilée se réfère aussi au principe de simplicité : « Qui voudra croire que la nature ait choisi de mouvoir à une vitesse inconcevable un nombre immense de très grands corps, pour produire un résultat auquel suffirait le mouvement modéré d’un seul corps tournant autour de son propre centre? » Il est à noter que les preuves expérimentales du mouvement de révolution annuel de la Terre autour du Soleil et de son mouvement de rotation propre en 24h ne seront acquises respectivement qu’en 1727 (mesure de l’aberration stellaire par Bradley) et 1851 (expérience du pendule de Foucault) !
Deux autres grands « révolutionnaires » de l’histoire des sciences, Newton et Einstein, ont également fait appel à plusieurs reprises au principe de simplicité pour étayer leurs nouvelles visions du monde. C’est par exemple grâce en partie au principe de simplicité que les modèles de « trous noirs » et ceux de « big-bang », à la base de l’astrophysique et de la cosmologie moderne, sont devenus crédibles : en effet, face à des modèles concurrents, ce sont eux qui réussissent le mieux à expliquer les observations par le nombre minimal d’hypothèses.

Bonjour cher monsieur Luminet ,
Je vous remercie sincèrement pour tout ce que vous partagez avec nous , vos lecteurs .
Le principe de simplicité m’a fait beaucoup réfléchir , ” les équations d’Einstein sont formellement plus compliquées que la loi de Newton. Elles sont néanmoins d’une plus grande simplicité ontologique” , l’étude de tout ce qui est, résumé en équations … J’adore ce que vous publiez et ce que vous nous faites découvrir, encore merci .
Merci beaucoup pour ces articles , parfait exemple de ” vulgarisation ” claire qui me donne envie d’approfondir par moi même pour combler les trous laissés par des études bien trop tôt abandonnées , erreur de jeunesse … merci encore
Merci de nous transmettre tant de vos connaissances, une question néanmoins, si vous permettez. Pour expliquer l’attraction universelle, vous choisissez l’image d’un tissu élastique déformé par un poids, et si je ne me trompe, vous dites que les masses “déforment l’espace”. J’aimerai avoir votre sentiment sur cette affirmation, et comment “déformer” une chose qui n’a pas de forme. D’avance merci.
J’aime bien la notion “d’élégance” utilisée aussi par les astrophysiciens pour illustrer ce principe de simplicité, avec une dimension esthétique en plus.
Et si le rasoir était pleinement appliqué en politique, ne tomberions-nous pas dans une société libertarienne (si on peut encore appeler ça une “société”) ? Ou ce serait encore confondre “simple” et “simpliste” ?
Et que penser d’une civilisation où tous le monde aurait ce principe dans les gènes, quelle sorte d’utopie – ou de cauchemar – aurions-nous ?
@ David DG
Il me semble que la société libertarienne ne peut pas être un état final, parce qu’elle est ontologiquement instable et aboutit à la “guerre de tous contre tous” de Hobbes. À moins qu’on impose des restrictions, donc une autorité, c’est-à dire une autre manière de signer la fin de cette société. Laissons donc le rasoir d’Occam être ce qu’il est depuis l’origine, un instrument d’analyse et non de prise de décision.
De plus, une société est définie par des relations. Or le credo libertarien exacerbe une liberté qui est justement une non-relation. Il y manque donc quelque chose, des valeurs, que la science n’a pas – ne doit pas avoir – pour mission ni compétence d’établir.
Selon moi, le principe de rasoir d’Ockham en Physique doit s’appliquer d’abord en faisant table rase de toute idéologie et théorie, cela parce qu’ensuite tout en apparence se complexifie.
Ainsi, à l’aide d’une hypothèse simple de l’univers, j’arrive à expliquer tous les phénomènes de la Physique “simplement”, sans mathéematiques.
Mon hypothèse est : L’univers consiste d’une dualité en mouvement.
Merci pour cette explication xdu rasoir d’ockham. Enfin je comprend ce principe dont j’ai si souvent entendu parler. Votre manière d’expliquer est à la fois simple et complète.