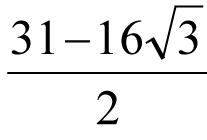Les sangakus japonaises sont de petits chefs d’œuvres aussi bien au niveau du raisonnement mathématique que de l’esthétique. Jean Constant, par exemple, s’en est fait une spécialité (voir l’image mise en avant). La sangaku suivante a été découverte par Hidetoshi Fukagawa.
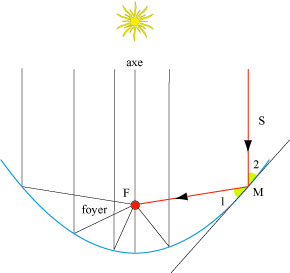
 Les deux triangles (rouge et vert) inscrits dans le carré jaune sont équilatéraux, quel est le rapport entre les rayons des cercles bleus ?
Les deux triangles (rouge et vert) inscrits dans le carré jaune sont équilatéraux, quel est le rapport entre les rayons des cercles bleus ?
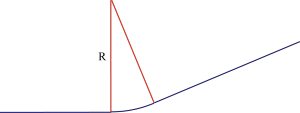
Rayon d’un cercle inscrit
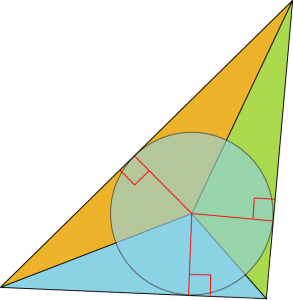
Les deux cercles sont inscrits dans deux triangles. Un théorème permet d’en calculer les rayons en fonction de leurs aires et de leurs périmètres. Plus précisément, le rayon du cercle inscrit dans un triangle est égal à deux fois la surface du triangle divisé par son périmètre, ce résultat est mis en évidence par un dessin : l’aire du triangle se décompose en trois triangles de même hauteur, le rayon du cercle inscrit. L’aire de chacun de ces triangles est donc égale au rayon du cercle inscrit multiplié par la longueur du côté opposé divisée par deux. En faisant la somme, le périmètre du triangle s’introduit naturellement .
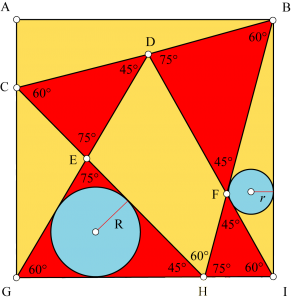
Plan d’attaque du problème
Pour calculer les rayons des deux cercles, il s’agit donc de calculer un certain nombre de longueurs de segments de la figure. L’idée pour les calculer vient si nous en oublions une partie. En utilisant les angles de 60° et de 45° en évidence, nous trouvons que les triangles rouges ont les mêmes angles et sont donc semblables.
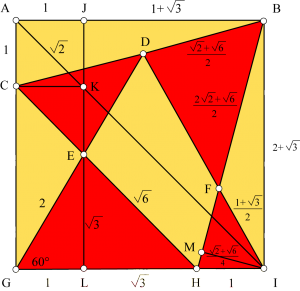
Grâce aux rapports de similitude et au théorème de Pythagore, les mesures de longueurs apparaissent progressivement, une d’entre elles (AC) ayant été choisie comme unité. Le dessin est utile pour suivre le raisonnement. Nous en déduisons progressivement les diverses longueurs importantes. Elles sont notées sur le dessin ci-dessous.
On en déduit les valeurs des deux rayons :
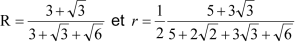 Un calcul algébrique
Un calcul algébrique
Un calcul algébrique permet de montrer que R = 2 r. Pour cette dernière étape, aucune visualisation n’est nécessaire et nous pouvons l’exécuter avec un logiciel de calcul formel. Ce dernier calcul nous entraîne vers les extensions algébriques, nous nous arrêterons à leur porte.
L’éventail de la geisha
Dans certaines sangakus, les auteurs ont clairement privilégié l’esthétique.
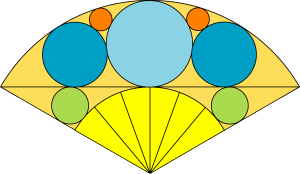
Par exemple, dans celui en forme d’éventail ouvert aux deux tiers ci-dessus, il s’agit de trouver le rapport entre les rayons des cercles verts et rouges. Ici encore, l’essentiel est d’introduire les bons points, qui ne sont pas directement visibles. On trouve :
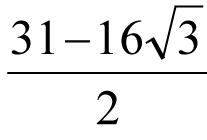


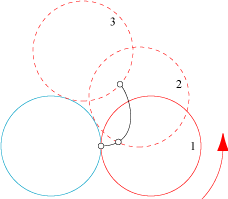



 Les deux triangles (rouge et vert) inscrits dans le carré jaune sont équilatéraux, quel est le rapport entre les rayons des cercles bleus ?
Les deux triangles (rouge et vert) inscrits dans le carré jaune sont équilatéraux, quel est le rapport entre les rayons des cercles bleus ?