Suite du billet précédent L’univers holographique (2) : la gravité quantique façon théorie des cordes

Dans le cadre de la théorie des cordes, il s’agissait dans un premier temps de retrouver les lois de la thermodynamique classique des trous noirs, c’est-à-dire savoir calculer, en termes de mécanique statistique quantique, leur entropie et leur température en fonction de leur aire et de leur gravité de surface. La tâche n’est pas aisée. Comme en thermodynamique, l’entropie mesure le nombre total d’états microscopiques internes correspondant à un état externe donné du trou noir, défini par ses trois paramètres (M, J, Q). Encore faut-il comptabiliser les « vrais » états microscopiques, c’est-à-dire les degrés de liberté ultimes sur lesquels il faut calculer l’entropie. Pour évaluer le contenu ultime en informations d’un élément de matière, c’est-à-dire son entropie thermodynamique, il faut en toute rigueur connaître ses constituants fondamentaux au niveau le plus profond de structuration. Dans le modèle standard de la physique des particules, les quarks et les leptons semblent suffisants pour coder toute l’information. Mais dans la théorie des cordes et sa théorie-mère (M-theory), les quarks et les leptons sont des états excités de supercordes, qui deviennent alors les constituants les plus élémentaires du monde physique.

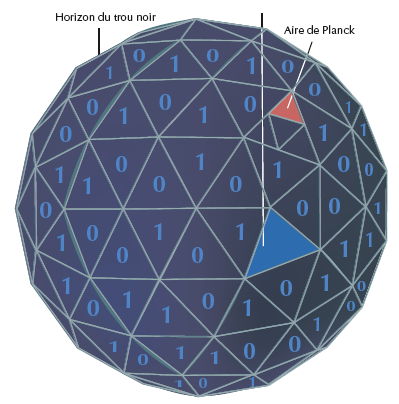
En 1993, Gerard t’Hooft (futur lauréat du prix de Nobel de physique 1999 pour ses travaux sur l’interaction électrofaible)  fut le premier à revisiter le travail de Hawking sur la thermodynamique des trous noirs dans le cadre de la théorie des cordes. Il calcula que le nombre total de degrés de liberté dans le volume d’espace-temps intérieur au trou noir était proportionnel à la superficie de son horizon[1]. La surface bidimensionnelle du trou noir peut être divisée en unités quantiques fondamentales appelées aires de Planck (10^–66 cm²). Du point de vue de l’information, chaque bit sous forme de 0 ou de 1 correspond à quatre aires de Planck, ce qui permet de retrouver la formule de Bekenstein-Hawking S = A/4 pour l’entropie. Tout se passe comme si l’information perdue pour un observateur extérieur – l’entropie du trou noir – portée initialement par la structure 3D des objets ayant traversé l’horizon des événements, était codée sur sa surface 2D à la façon d’un hologramme, et t’Hooft en conclut que l’information avalée par un trou noir devait être intégralement restituée lors du processus d’évaporation quantique.

C’est dans le cadre encore plus général de la théorie M qu’en 1996, Andrew Strominger et Cumrun Vafa sont parvenus à calculer l’entropie d’un trou noir chargé “extrémal” en dimension 5. Un trou noir chargé extrémal est décrit par une solution de Reissner-Nordström dans laquelle la masse M et la charge électrique totale Q du trou noir extrême sont liées par la relation M² = Q². Précisons que ce type de trou noir supersymétrique n’a rien à voir avec les trous noirs astrophysiques que l’on rencontre dans la nature, mais il permet de simplifier les calculs! Strominger et Vafa ont donc considéré le trou noir comme un gaz de cordes ; en comptant les états quantiques associés aux vibrations des cordes, ils ont pu retrouver la formule de Bekenstein-Hawking donnant l’entropie d’un trou noir en fonction de l’aire de son horizon, sa température en fonction de sa gravité de surface, ainsi que les caractéristiques du rayonnement de Hawking[2].

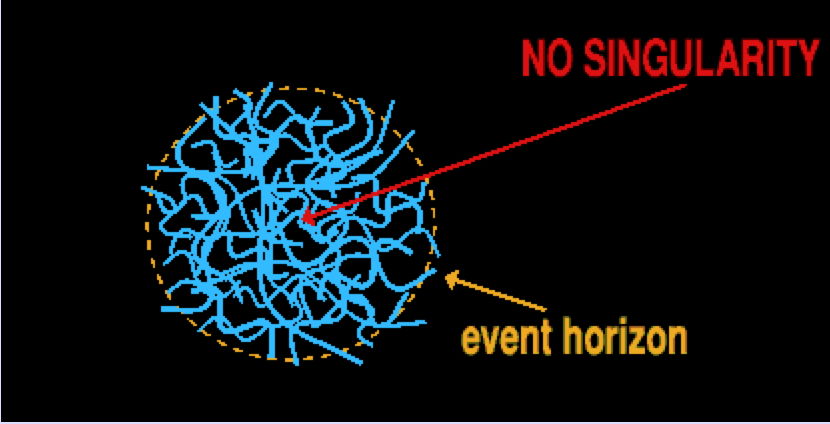
A la suite de ces résultats encourageants, de nombreux travaux ont réussi à reproduire l’entropie microscopique de trous noirs un peu plus généraux, en 4 et 5 dimensions, affectés de charges électriques et de moments angulaires proches de l’extrémalité[3]. On pouvait dès lors considérer l’évaporation d’un trou noir comme l’émission de cordes fermées (des gravitons) à partir d’un système de branes représentant le trou noir.

A ce moment, la théorie des cordes semblait prête à résoudre le paradoxe de l’information des trous noirs, c’est-à-dire prouver que le rayonnement de Hawking contient bien toute l’information relative à ses propriétés internes. Le programme s’est toutefois révélé trop optimiste. On s’est vite aperçu que tout contrôle calculatoire était perdu dès qu’on s’éloigne significativement des conditions d’extrémalité, de sorte que le trou noir le plus simple du point de vue de la relativité générale, la solution de Schwarzschild, échappe au calcul des micro-états – sans parler du trou noir astrophysique le plus réaliste, décrit par la solution de Kerr.

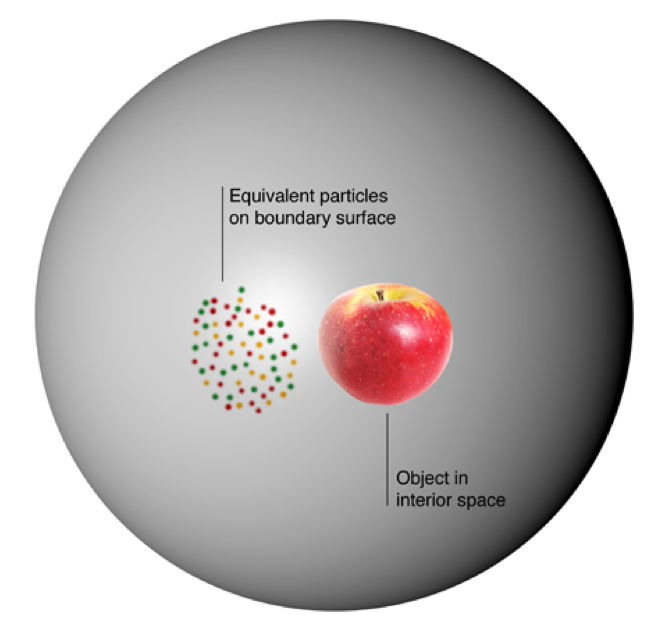
Malgré tout, l’idée que la quantité d’informations détenue dans un trou noir dépende de l’aire de son horizon des événements et non pas de son volume suscita un extraordinaire engouement. Reprise et largement développée par Leonard Susskind[4], elle est devenue connue sous le nom de principe holographique, avec la folle ambition de se généraliser à tout système physique occupant un volume d’espace-temps : le principe postule alors que la physique complète – incluant les phénomènes gravitationnels – dans ce volume peut être entièrement décrite par une autre théorie physique opérant seulement sur sa frontière !

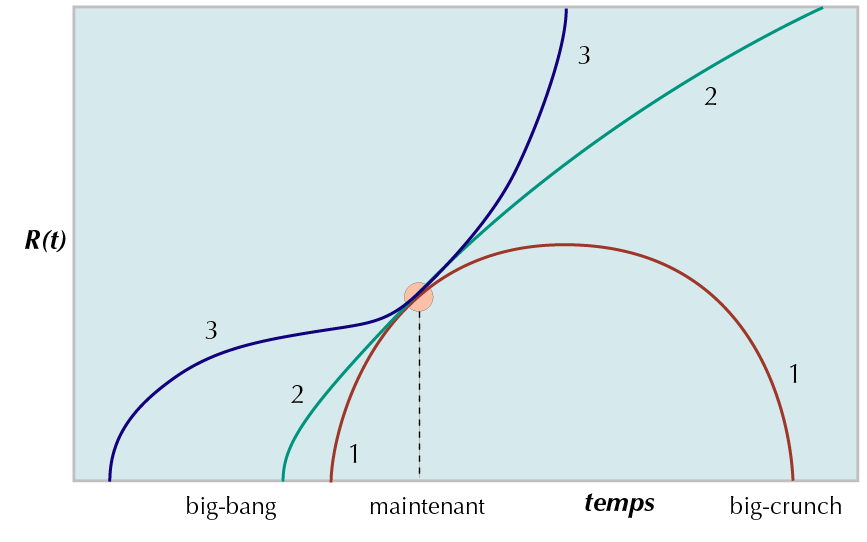
On pouvait d’ores et déjà soupçonner que le principe holographique ne s’applique pas à notre univers dans son ensemble. A notre connaissance, ce dernier est un espace-temps à quatre dimensions macroscopiques ; s’il était holographique, un ensemble de lois physiques alternatives s’appliquant sur sa frontière tridimensionnelle existerait quelque part et équivaudrait à la physique quadridimensionnelle usuelle. Mais quelle surface pourrions-nous prendre comme enveloppe de notre l’espace-temps ? Le modèle cosmologique standard est une solution de Friedmann-Lemaître ouverte, de courbure spatiale proche de zéro et en expansion accélérée, et qui, contrairement au cas du trou noir, ne possède pas de frontière définie où placer une quelconque hologramme. De plus, la limite holographique sur l’entropie déduite des trous noirs est pulvérisée dans un univers spatialement homogène et isotrope en expansion : l’entropie d’une région d’espace-temps non effondrée en trou noir, remplie de matière et de rayonnement, est vraiment proportionnelle à son volume, pas à l’aire de son enveloppe.

La suite est ici :  La conjecture de Maldacena

Références

[1] Gerard ‘t Hooft, “Dimensional Reduction in Quantum Gravity”, arXiv :gr-qc/9310026 (1993).

[2] Andrew Strominger and Cumrun Vafa, “Microscopic origin of the Bekenstein–Hawking entropy”, Phys. Lett. B 379 (1996) : 99–104.

[3] Pour une revue : A. Dabholkar and S. Nampuri, “Quantum black holes”, Lect. Notes Phys. 851 (2012) : 165-232.

[4] Leonard Susskind, “The World as a Hologram”, Journal of Mathematical Physics 36 (11) (1995): 6377–6396.