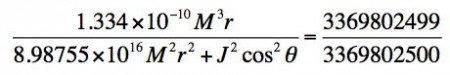Suite du billet précédent La physique étrange d’Interstellar (3/6)
En novembre 2014, le film de science-fiction Interstellar (réalisation Christopher Nolan, Warner Bros Pictures, 169 minutes, 2014) sortait sur nos écrans. Véritable « blockbuster » hollywoodien, il a suscité un énorme battage médiatique, comme en témoignent les innombrables forums de discussion et articles de presse ayant fleuri au cours des jours, semaines et mois qui ont suivi. A la demande de la revue de langue anglaise Inference : International Review of Science, j’ai par la suite fait un travail d’analyse scientifique beaucoup plus développé et approfondi, publié au printemps 2015. Je vous en livre la traduction française, découpée en 6 billets. Celui-ci est le quatrième.
Dilatation temporelle
La théorie de la relativité restreinte d’Einstein prédit que des observateurs placés dans des référentiels différemment accélérés perçoivent le temps différemment. Ce phénomène bien connu de « dilatation » temporelle a été vérifié expérimentalement à un haut degré de précision. Les conséquences de la dilation temporelle se font sentir tout au long de l’histoire d’Interstellar.

Près de l’horizon des événements d’un trou noir, où le champ gravitationnel est énorme, la dilatation temporelle est également énorme. Les horloges sont fortement ralenties par rapport aux horloges lointaines. Une heure sur Miller (temps propre de Miller) équivaut à sept années sur Terre. Ceci correspond à un facteur de dilatation de 60 000. Bien que la dilatation temporelle tende vers l’infini quand l’horloge tend vers l’horizon des événements, un facteur de dilatation de 60 000 est impossible pour une planète en orbite stable autour d’un trou noir.
Dans son livre, The Science of Interstellar, Kip Thorne explique qu’un facteur de dilatation temporelle de cette grandeur était une exigence non négociable de la part du réalisateur[1]. Après quelques heures de calcul, Thorne est parvenu à la conclusion que le scénario, bien que très peu vraisemblable, était marginalement possible. Le facteur-clé est la période de rotation du trou noir. Un trou noir de Kerr (tournant) se comporte très différemment d’un trou noir de Schwarzschild (statique). L’équation de dilatation temporelle dérivée de la métrique de Kerr s’écrit:
1 – (dτ/dt)2 = 2GMr/c2rho2, où rho2 = r2 + (J/Mc)2cos2θ.
En substituant dτ = 1 heure et dt = 7 ans, on obtient: