Ecologie, Mathématiques, Nature

Un lemming ne se suicide jamais !

Laisser un commentaire

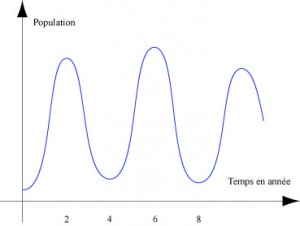
Selon la légende, le lemming – un petit rongeur ressemblant à un hamster, vivant dans les régions nordiques comme la Suède, le Canada et le Groenland – est d’un altruisme tel qu’il se suicide en masse pour le bien de sa communauté quand celle-ci devient trop nombreuse. Même si l’idée de suicides d’animaux est étonnante, l’évolution de la population lemming suit effectivement une courbe étrange.

Évolution de la population de lemmings, on note un cycle de quatre ans. Le rapport entre les minima et maxima est de 1 à 1000, ce qui peut faire penser à une extinction des lemmings.

Un film “documentaire”

Cette courbe se recopie elle-même tous les quatre ans mais, quand la population lemming est à son minimum, on peut penser à une extinction car le rapport entre minimum et maximum est de 1 à 1000 environ. En fait, il n’en est rien et ils reviennent toujours avec une périodicité de quatre ans, et ceci dans toutes les contrées où ils vivent. En 1958, dans White Wilderness, les studios Walt Disney ont présenté des vagues de lemmings se précipitant dans la mer du haut d’une falaise. Bien entendu, il s’agissait d’un trucage cinématographique. Un examen attentif du film montre d’ailleurs que l’on ne voit jamais plus de 12 lemmings simultanément à l’écran. S’il n’en est pas à l’origine, ce film « documentaire » a sans doute conforté la fable selon laquelle le lemming se suicide en masse quand la population de sa communauté devient trop importante pour la région où il habite.

Un modèle mathématique

Un labbe en train de dévorer un bébé manchot. @ Hervé Lehning

En fait, ces fluctuations peuvent s’expliquer par la présence d’un prédateur exclusivement dévoué au lemming, l’hermine. Ce petit rongeur en a d’autres, comme les renards, les labbes et les harfangs, mais ceux-ci mangent ce qu’ils trouvent le plus facilement alors que l’hermine ne chasse que le lemming. Elle provoque ainsi sa quasi extinction … et donc la sienne en conséquence, ce qui laisse aux survivants la chance de reconstituer le peuple lemming et à l’histoire de recommencer éternellement. Cette façon, somme toute littéraire, de présenter le phénomène permet de comprendre son côté qualitatif. Un modèle mathématique précise son côté quantitatif. Nous en proposons une version très rudimentaire, car il ne tient pas compte des saisons, même s’il suffit cependant à vérifier le phénomène.

Une hermine.

Admettons qu’en l’absence de prédateurs, la population des lemmings croisse hebdomadairement avec un taux dépendant de la natalité et de la mortalité naturelles. La présence de l’hermine change la donne, et ce taux doit être minoré d’une valeur proportionnelle au nombre d’hermines. Autrement dit, un nouveau coefficient rentre en jeu, qui correspond à la prédation. Pour fixer les idées, si le taux de croissance naturelle des lemmings est égal à 1,05 et le taux de prédation égal à 0,0001, une population de 1000 hermines donne un taux de croissance de la population lemming égal à son taux naturel 1,05 moins la prédation, soit 0,0001 multiplié par 1000. Le taux total est donc égal à 1,04. Si la population lemming est de 40000 individus, elle est de 40000 multiplié par 1,04 la semaine suivante, soit 41600 individus.

Pendant ce temps, la population d’hermines évolue aussi du fait de son taux de croissance naturel qui doit être majoré d’une valeur proportionnelle au nombre de lemmings. Si le taux de croissance naturel est de 0,97 et le taux dû à l’alimentation (c’est-à-dire à la prédation) est de 0,000001, le taux de croissance des hermines est de 0,97 plus 40000 multiplié par 0,000001, soit 1,01. La population d’hermines la semaine suivante est donc égale à 1000 multiplié par 1,01 soit 1010.

Gestion des animaux dans les parcs naturels

Les mêmes calculs peuvent être repris la semaine suivante et les quatre paramètres ajustés pour correspondre à la réalité constatée sur le terrain, ce que nous avons fait d’ailleurs. Les valeurs ci-dessus donnent bien une périodicité de quatre années environ. Ces formules sont générales et valables pour d’autres couples proies / prédateurs. Elles servent pour la gestion des animaux dans les parcs naturels. Par exemple, si on constate un risque de fort accroissement du nombre de prédateurs, la direction du parc peut décider d’autoriser la chasse d’un certain nombre d’animaux pour éviter un cycle d’évolution des populations chaotique.

Cryptologie, Histoire

Le chiffre de la reine Marie-Antoinette

2 commentaires

Pour qu’elles ne puissent pas être interceptées, Marie-Antoinette chiffrait ses lettres. La méthode qu’elle utilisait était a priori excellente… mais avec une erreur majeure : elle ne chiffrait qu’une lettre sur deux.

Chiffre de Vigenère

Marie-Antoinette chiffrait ses lettres par substitution poly-alphabétique, selon la méthode décrite par Blaise de Vigenère plus précisément. Cette méthode suppose de disposer d’une table de chiffrement, si possible une par destinataire. Voici comment se présentait ces tables :

Une table de chiffrement utilisée par Marie-Antoinette. @ Archives nationales

On notera que ce tableau ne contient que 22 lettres, les lettres manquantes sont J, K, U et W, ce qui correspond à un usage venant du latin où I et J d’un côté, U et V de l’autre sont confondues. K peut être remplacé par C et W par V.

Clef de chiffrement

L’utilisation de ce tableau pour chiffrer demande une clef secrète qu’on partage avec le destinataire. Par exemple, si la clef est sel, pour chiffrer la première lettre, on utilise la ligne dont la première colonne est ST, D est alors changé en N (et N en D), E en O, etc. Pour chiffrer la seconde, on utilise la ligne dont la première colonne est EF.

Utilisation correcte

Pour chiffrer une phrase comme je vous aime, on peut construire un tableau à 10 lignes et 3 colonnes :

J E V O U S A I M E
S E L S E L S E L S
S T D E F B X Z Q O

 

Le message chiffré est donc stdefbxzqo. Si vous essayez de chiffrer une lettre ainsi, vous verrez la difficulté d’éviter les erreurs. C’est pour cela que, on ne sait quel cryptologue avait conseillé à Marie-Antoinette de ne chiffrer qu’une lettre sur deux ce qui, en fournissant des repères, simplifie grandement le chiffrement mais l’affaiblit tout aussi grandement. Nous allons voir pourquoi.

Utilisation par Marie-Antoinette

Le tableau devient ainsi :

J E V O U S A I M E
S E L S E
J O V M U B A S M T

 

Le message chiffré est maintenant jovmubasmt. On peut examiner des lettres chiffrées ainsi par Marie-Antoinette aux Archives nationales, comme la suivante :

Lettre de Marie-Antoinette au comte de Fersen où on voit qu’elle ne chiffrait qu’une lettre sur deux. @ Archives nationales

Décryptement

Le décryptement sans connaître la clef est ainsi facilité, surtout si on connaît le tableau de chiffrement. C’est ici que des talents de cruciverbiste sont utiles. En effet, on peut deviner un mot si on en connaît une lettre sur deux comme ici J-V-U-A-M, qui est transparent pour tout amateur de mots croisés. Ensuite, on sait que la première lettre de la clef transforme E en O ce qui ne se produit que pour ST, en continuant ainsi, on décrypte le message quel que soit sa longueur.

 

Mathématiques

L’art de moyenner

Un commentaire

Quand on veut calculer la taille moyenne des Français, le principe est simple. On mesure la taille de chaque français de plus de 18 ans (les mesurer depuis la naissance fausserait la moyenne), on fait le total de ces tailles et on divise par le nombre total de Français adultes. On trouve un nombre comme 176 cm qui est donc la taille moyenne des Français adultes. On peut recommencer avec les Françaises, on trouve 163 cm.

Pour calculer la moyenne de la taille des girafes, on ne retient que la taille des adultes. @ Hervé Lehning

La moyenne arithmétique

En mathématiques, on parle de moyenne arithmétique. Par exemple, la moyenne arithmétique des dix nombres du tableau ci-dessous est égale à leur somme 618 divisée par 10 soit 61,8.

82

 71 98 64 77 39 86 69 22

10

La vitesse moyenne

Prenons l’exemple du calcul d’une vitesse moyenne sous la forme d’une petite énigme :

Deux villes A et B sont distantes de 100 km, un automobiliste effectue le trajet de A à B en une heure et le retour en deux heures. Quelle est sa vitesse moyenne ?

Comme le premier trajet s’effectue à 100 km/h de moyenne et le retour à 50 km/h, on peut être tenté de faire la moyenne arithmétique des deux nombres et répondre 75 km/h. En fait, ce résultat est faux. Un raisonnement plus correct consiste à dire que l’automobiliste a parcouru 200 km en trois heures et donc que sa vitesse moyenne a été de 200 / 3 = 67 km/h (en arrondissant). La différence est notable.

La moyenne harmonique

Cette nouvelle moyenne, adéquate pour calculer les vitesses, est appelée la moyenne harmonique. Si on considère une suite finie de n nombres a, b, etc. les moyennes arithmétique et harmonique A et B sont données par les formules :

A = (a + b + …) / n   et   1 / H = (1/a + 1/b + …) / n

Il existe toute sorte d’autres moyennes correspondantes chacune à la nature des quantités à moyenner. On ne moyenne pas de même des longueurs, des poids, des vitesses, des températures, etc.

Cryptologie

Les messages chiffrés du Figaro en 1890

Un commentaire

En 1890, le Figaro contenait une rubrique de correspondances personnelles dont certains messages étaient a priori incompréhensibles. Voici une partie de ceux du premier janvier :

La rubrique correspondances personnelles du Figaro, du premier janvier 1890. @ BNF

Chiffre de César

Parmi des messages écrits en style télégraphique, nous en trouvons deux, manifestement entièrement chiffrés. Dans le premier, bonne année est devenue cpoof booff. Autrement dit, il s’agit d’un simple décalage (ou chiffre de César) et le tout signifie : Bonne année d’un ami bien malheureux.

Substitution alphabétique

Le message suivant (d’indicatif LILI) est bien plus intéressant à décrypter. De prime abord, nous pouvons juste penser que le chiffre 2 représente e, du moins si la méthode de chiffrement utilisée est une substitution alphabétique car il s’agit du symbole majoritaire. Heureusement, en feuilletant le Figaro des jours suivants, nous rencontrons un grand nombre de messages sous le même indicatif LILI. Nous nous arrêtons naturellement le douze janvier sur un message à moitié chiffré, une erreur classique de chiffrement.

La rubrique correspondances personnelles du 12 janvier 1890 dans le Figaro. @BNF

Écrit en style télégraphique, le message commence par votre pensée ne me quitte pas, est tout mon bonheur, voudrais vous voir, la suite qu’on veut cacher est 32. u. 13. n2. La disposition des deux 2 nous fait penser à je t’aime si i et j sont assimilés comme ils le sont en latin. Les chiffres 1, 2 et 3 représentent donc les voyelles a, e et i, les lettres u et n représentent t et m. La méthode de chiffrement semble être de représenter chaque voyelle par son numéro d’ordre et chaque consonne par la lettre qui la suit. Pour vérifier cette hypothèse, nous revenons au message du premier janvier :

1.w. m2. qs2n32s n2t w25y c400. 100. w45e. 2us2. u. qs2t e w. o. q20t r s2w.

En le déchiffrant selon la méthode que nous venons d’exposer, on obtient une phrase en style télégraphique :

a v le premier mes veux bonn ann voud etre t pres d v n pens q rev

ce qui signifie probablement :

À vous le premier, mes vœux de bonne année. Je voudrais être tout près de vous. Ne pense qu’un rêve !

Même si une erreur a pu se glisser dans la dernière phrase, le sens des deux premières prouve que notre hypothèse est correcte. De façon étonnante, la méthode de décryptement fonctionne pour un autre message du douze janvier, celui portant l’indicatif Bleuet :

 Complètement rétabli. Rentre à Paris semaine prochaine, je serai heureux de pouvoir vous voir mercredi 4 h. Mille amitiés.

Intérêt

Au-delà des curieux, ces messages chiffrés pourront intéresser les historiens qui y verront un témoignage des rapports humains à cette époque, surtout de ceux que l’on souhaitait cacher.

Ecologie, Mathématiques, Nature, Réflexions

L’effet papillon d’Edward Lorenz

Laisser un commentaire

L’effet papillon est un exemple très rare d’expression venant des mathématiques ayant eu un succès médiatique incontestable. Tout le monde connaît l’effet papillon : petites causes, grandes conséquences comme certains l’ont chanté.

L’origine de la métaphore

En 1972, à une conférence de météorologie, Edward Lorenz a présenté un exposé sous un titre qui a frappé les esprits :

Le battement d’ailes d’un papillon au Brésil peut-il provoquer une tornade au Texas ?

Cette métaphore n’est toutefois pas de Lorenz mais d’un organisateur de la conférence, Philip Merilees. Pour justifier sa question, Lorenz utilisait un modèle mathématique très simplifié de l’atmosphère terrestre où il n’avait conservé que trois inconnues pouvant donc être représentées par un point de l’espace. Il s’agit de ce qu’on appelle en mathématiques un système dynamique. On part d’une condition initiale, c’est-à-dire d’un point représentant l’état du système à l’instant initial et le modèle nous donne les états du système aux instants qui suivent, théoriquement indéfiniment.

L’attracteur de Lorenz

Dans le cas du modèle de Lorenz, chaque condition initiale donne une orbite ressemblant grossièrement aux deux ailes d’un papillon. De plus, toutes les orbites s’agglutinent sur un même objet également en forme de papillon, qu’on nomme l’attracteur de Lorenz.

L’attracteur de Lorenz a une forme de papillon. © Hervé Lehning

Cette forme explique peut-être le choix de cet insecte par Merilees. Peu importe, le papillon a séduit bien au-delà de la sphère mathématique sans que, pour autant, le message de Lorenz soit complètement compris. En effet s’il mettait l’accent sur la sensibilité aux conditions initiales, un faible changement pouvant avoir de grosses conséquences, il corrigeait immédiatement l’idée de la soumission au hasard d’un battement d’aile de papillon par :

J’avance l’idée qu’au fil des années de petites perturbations ne modifient pas la fréquence d’apparition d’événements comme les tornades : la seule chose qu’ils peuvent faire, c’est de modifier l’ordre dans lequel ces événements se produisent.

Nous sommes ainsi très loin de la notion couramment vulgarisée : petites causes, grandes conséquences. Dans la pensée de Lorenz, le chaos sert à la prévision, les orbites ne sont pas aléatoires, elles se situent sur l’une ou l’autre aile de l’attracteur, le passage de l’une à l’autre semblant aléatoire. Cette conception éclaire l’idée a priori paradoxale qu’on puisse étudier l’évolution du climat sans pour autant être capable de prévoir le temps du mois suivant.

Arts, Mathématiques, Regard sur le monde

La balustrade hyperbolique du jardin du Luxembourg

Laisser un commentaire

Au Luxembourg, des balustrades circulaires du XVIIIe siècle ferment la perspective des jardins.

Rien que des coniques

On les voit donc sous forme de coniques, c’est-à-dire de sections planes d’un cône.

Balustrade hyperbolique au Luxembourg © Hervé Lehning

Vues de l’intérieur, il s’agit donc d’une hyperbole parfaite, que l’on peut comparer avec la bouche d’égout elliptique au sol. La parabole quant à elle appartient au monde des idées, cas limite entre l’hyperbole et l’ellipse, que l’on pourrait voir en se positionnant parfaitement sur la colonnade.

Arts, Graphismes, Mathématiques

Les surfaces minimales de Patrice Jeener

Laisser un commentaire

Patrice Jeener est un graveur tombé amoureux des mathématiques en visitant l’institut Henri Poincaré quand il était étudiant aux beaux-arts. Il suivait ainsi la trace de Man Ray, qui découvrit les modèles de l’institut dans les années 30 et s’en inspira pour sa série de tableaux équations shakespeariennes comme celui-ci intitulé le roi Lear :

Le roi Lear © Man Ray

Les surfaces minimales

Patrice Jeener s’est particulièrement intéressé aux surfaces minimales, c’est-à-dire aux surfaces dont les aires sont minimales pour un bord donné. On peut matérialiser la plupart d’entre elles par des bulles de savon s’appuyant sur un contour, car le film de savon tend à minimiser son énergie, donc sa surface. Elles ont des applications pratiques mais notre propos n’est pas là. Sur la photographie ci-dessous, notez la petite tige en bas à droite qui permet de tenir l’objet quand on le trempe dans l’eau savonnée :

Nous n’écrirons pas leurs équations ici, nous nous contenterons d’en admirer l’esthétique à travers quelques gravures.

Surface minimale de Schwartz © Patrice Jeener

L’étude des surfaces réservent quelques surprises comme l’apparition surprenante d’une chouette là où l’on attendait une simple surface minimale. Ce genre de surprises explique sans doute ce vers de Lautréamont :

O mathématiques sévères, je ne vous ai pas oubliées, depuis que vos savantes leçons, plus douces que le miel, filtrèrent dans mon cœur, comme une onde rafraîchissante.

Surface minimale à la chouette © Patrice Jeener
Graphismes, Mathématiques

Décrypter l’art concret

Laisser un commentaire

Philippe Leblanc a exposé chez Philomuses, au quartier latin à Paris, une série d’œuvres a priori abstraites. Les titres même font mystère. Par exemple, la suivante se nomme Chinacci 25.

Chinacci 25 © Philippe Leblanc

L’écriture chinoise ancienne des nombres

En lisant le tableau en colonne, le mathématicien sera frappé par la régularité des premiers termes : 1, 1, 2, 3, 5 où chaque nombre est la somme des deux précédents. Le suivant peut facilement être interprété comme un 8. De fait, le tableau de Philippe Leblanc utilise un système d’écriture des nombres inventé en Chine quelques siècles avant Jésus-Christ. À cette époque, les Chinois comptaient au moyen de baguettes et non de bouliers comme plus tard. Ils imaginèrent ainsi une façon d’écrire les nombres. Pour cela, ils utilisaient deux notations qu’ils alternaient pour éviter les confusions entre unités, dizaines, centaines, etc. Voici donc les chiffres de 1 à 9 écrits de deux façons différentes.

La suite de Fibonacci

On s’aperçoit ainsi que le tableau représente les 25 premiers termes de la suite de Fibonacci, le dernier terme en bas à droite du tableau valant 75025. Le titre de l’œuvre prend alors son sens, Chinacci 25 étant une contraction de Chinois-Fibonacci, 25 premiers termes. Après cette première analyse, on peut se demander ce que signifient les différences de couleurs, entre jaune et bleu. Pour le voir, il faut réaliser que les bâtons de l’œuvre sont découpés au laser dans une tôle d’acier, qui cache une boîte lumineuse. C’est le fond de cette boîte qui est peinte selon plusieurs bandes verticales dont les largeurs suivent également la suite de Fibonacci : une bande de largeur X en jaune, une deuxième bande de largeur X en bleu foncé, une bande de largeur 2X en jaune orangé, une quatrième bande de largeur 3X en bleu clair. La deuxième œuvre Mayanacci 25  s’éclaire alors d’elle-même.

Mayainacci 25 © Philippe Leblanc

La suite de Fibonacci s’y écrit en lignes puisque la première se lit 1, 1, 2, 3 en comptant les points. La barre qui suit signifie alors probablement 5. On peut ainsi décrypter les nombres suivants. Il s’agit en fait de l’écriture des nombres qu’utilisaient les Mayas, en base vingt. Les unités, les vingtaines, etc. s’empilent de bas en haut. Les couleurs respectent une règle différente de celle du tableau précédent puisque, dans chacune des cinq lignes et des cinq colonnes, on trouve une et une seule fois chacune des cinq couleurs présentes.

Mathématiques, Mes publications

Toutes les mathématiques du monde

8 commentaires

Un pari : présenter le côté culturel des maths sans se perdre dans la technique

Mon pari, en écrivant Toutes les mathématiques du monde, était de présenter ce que sont les mathématiques sans entrer dans la technique. Comment ont-elles évolué de questions concrètes comme le dénombrement et l’arpentage jusqu’à devenir l’archétype de l’abstraction ? Pourquoi ont-elles envahi le monde contemporain ? Peut-on comprendre ce monde sans culture mathématique ? Suivre un simple débat sans cela ? Notre réponse est « non » mais cette culture mathématique est accessible à tous, sans pour autant devenir un spécialiste.

Arts, Photographies

Les colombes givrées

2 commentaires

Ce glaçon étrange, que j’ai nommé les colombes givrées s’était détaché d’un glacier pour tomber dans un fjord et était venu s’échouer sur une plage où je venais de débarquer. Un rayon de soleil illuminait cette œuvre d’art éphémère que le hasard avait façonnée, l’art consistait à trouver le bon angle permettant de capturer la lumière malgré la légère pluie qui tombait.

Les colombes givrées © Hervé Lehning

Le glacier à l’origine du glaçon

Voici le front du glacier d’où s’échappent les glaçons plus ou moins gros :

Le front du glacier © Hervé Lehning

Comme on peut le voir sur cette photographie, la vie animale est riche à l’endroit où le glacier se jette dans la mer. Les oligo-éléments charriés par le glacier attirent le plancton, qui attire le poisson, qui attire des oiseaux pêcheurs et quelques phoques.

Comment comprendre le monde moderne sans culture mathématique ? Accéder à celle-ci n’exige cependant pas d’apprendre à résoudre la moindre équation.