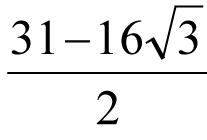Quel rapport entre la bataille de Tannenberg (26-29 août 1914) et la bataille de Varsovie (13-25 août 1920) ? Dans les deux cas, les armées russes furent défaites par des armées très inférieures en nombre du fait de l’interception de leurs communications radios.
La bataille de Tannenberg
En août 1914, l’entrée en guerre de la Russie se fit dans une telle précipitation qu’aucun matériel cryptographique n’avait été livré si bien que les communications russes se faisaient en clair par radio. Autrement dit, les Allemands étaient invités aux réunions d’état-major des Russes. Le général en chef allemand sut utiliser cet avantage pour diviser les armées russes et anéantir l’une d’entre elles.
Le “miracle” de la Vistule
Si le renseignement allemand avait été particulièrement aidé par l’absence de chiffrement des messages russes en 1914, c’est par le décryptement que, en 1920, les Polonais s’invitèrent aux réunions d’état-major russe avec un résultat identique. La victoire qui s’ensuivit fut attribué par le clergé polonais à une intervention divine d’où le nom qui lui fut attribué de miracle de la Vistule.
L’excellence polonaise en matière de cryptologie
Le miracle de la Vistule est donc avant tout un miracle du décryptement.

L’excellence du bureau du chiffre polonais se poursuivit jusqu’au début de la Seconde Guerre mondiale puisque le premier décryptement d’Enigma fut un succès conjoint de l’espionnage français et du génie de trois mathématiciens polonais : Marian Rejewski (1905 – 1980), Jerzy Rozycki (1909 – 1942) et Henryck Zygalski (1908 – 1978). L’espionnage a fourni les tables de chiffrement de l’armée allemande de 1931 à 1938. Les mathématiques ont permis, grâce à ce renseignement, de reconstituer les câblages de la version militaire de l’Enigma et de fabriquer des répliques d’Enigma dès 1933. Les messages furent alors déchiffrés régulièrement. Les mathématiciens polonais cherchèrent à pouvoir se passer des tables de chiffrement, ce qu’ils réussirent à faire, en particulier en créant une machine, la bomba. Elle permettait de trouver la clef du jour en quelques minutes. Après la défaite de la Pologne puis celle de la France, les résultats polonais furent livrés aux Britanniques. Le mathématicien Alan Turing (1912 – 1954) et son équipe de Bletchley Park reprirent avec succès le décryptement en l’améliorant et en l’adaptant aux complexifications successives d’Enigma. La guerre fut probablement écourtée de deux ans grâce au décryptement.


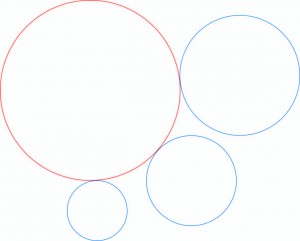
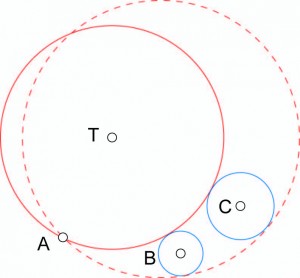






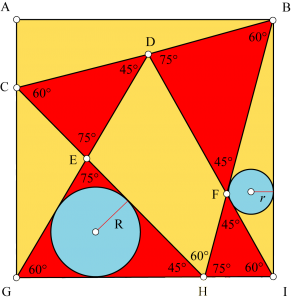
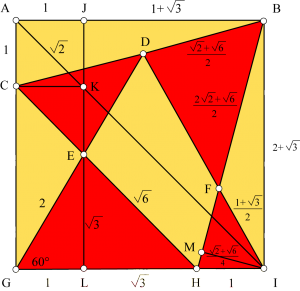
 Les deux triangles (rouge et vert) inscrits dans le carré jaune sont équilatéraux, quel est le rapport entre les rayons des cercles bleus ?
Les deux triangles (rouge et vert) inscrits dans le carré jaune sont équilatéraux, quel est le rapport entre les rayons des cercles bleus ?