La première référence à un carré magique est une légende chinoise associée à la rivière Luohe, un affluent du fleuve Jaune, qui eut son heure de gloire pendant le millénaire précédant notre ère, quand la ville de Luoyang, bâtie sur ses rives, était capitale de la Chine. Ses multiples versions parlent toutes d’une tortue portant d’étranges inscriptions sur son dos.
Une tortue légendaire
Pour calmer le dieu de la rivière, à chaque inondation, les habitants d’un village menacé d’être englouti lui offraient des sacrifices en vain. Cependant, ils remarquèrent qu’à chaque fois, une tortue venait sur les lieux du sacrifice et repartait. Le dieu du fleuve n’en tenait cure jusqu’à ce qu’un jour, un enfant remarqua des formes curieuses sur le dos de l’animal.
Dans chaque ligne, chaque colonne et chaque diagonale, le nombre était le même. Ainsi, les villageois comprirent que le dieu du fleuve demandait quinze sacrifices, et purent l’apaiser…
Les carrés magiques
Ce carré est depuis appelé « carré Luoshu » du nom de la rivière. Il a vite conquis le Moyen-Orient puis la Grèce où il était connu de Pythagore. Il est toujours utilisé comme amulette porte-bonheur et dans des exercices divinatoires. De nos jours, ces carrés où les sommes des nombres des lignes, colonnes et diagonales sont identiques sont appelés « carrés magiques », preuve de l’antique croyance. On peut de plus ajouter une contrainte, celle de n’utiliser que les premiers nombres donc ceux de 1 à 9, dans le cas d’un carré d’ordre trois, et ceux de 1 à 16 pour ceux d’ordre quatre. Avec cette dernière contrainte, il n’existe aucun carré d’ordre deux : vous pouvez disposer les nombres de 1 à 4 comme vous le voulez, le carré formé ne sera jamais magique. De ce fait, les pythagoriciens en faisaient un symbole du chaos. Aux symétries près, le carré d’ordre trois est unique, c’est le Luoshu (voir à la fin de cet article). De nos jours, les ésotériques préfèrent l’écrire de façon à faire apparaître le nombre 618 en première ligne car ce sont les premières décimales du nombre d’or. Pour eux, il devient ainsi doublement magique.
Le carré magique d’ordre 3
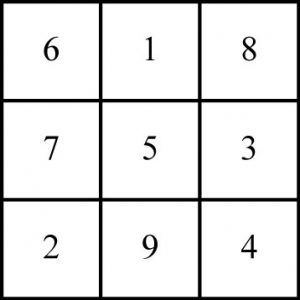
Schéma de preuve
Si les cases du carré contiennent tous les nombres de 1 à 9, la somme de toutes les cases est 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9, c’est-à-dire 45. Les sommes de toutes les rangées et des diagonales sont donc égales à 45 divisé par 3, soit 15. Selon leur place, les nombres participent à 4, 3 ou 2 sommes égales à 15. En partant d’un nombre initial, comme 1, nous examinons le nombre de décompositions donnant 15 en tout. Pour 1, il en existe deux : 9 + 5 et 8 + 6. En opérant ainsi, nous obtenons le tableau :
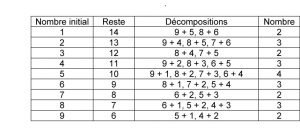
Ce tableau permet de remplir le carré.
