La voûte semble être née plate. Pour permettre une ouverture dans un mur, traditionnellement, on posait au-dessus une pierre assez longue en guise de linteau, comme dans le cas de cette porte dans les ruines de Délos en Grèce.

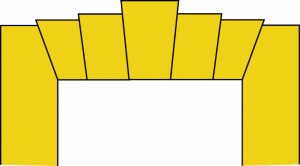
S’ils ne disposaient pas de pierres assez longues, dès l’Antiquité, les architectes ont trouvé un moyen d’y pallier en utilisant plusieurs pierres plus petites disposées de façon à ce que le poids de l’ensemble bloque le linteau. La pierre centrale, en coin dans le dispositif, est appelée la clef de voute. Il est probable que cette méthode ait été trouvée par essais et erreurs même si elle s’explique très bien par la pesanteur, en calculant le bilan des forces exercées, ce que les ingénieurs savaient faire à l’époque d’Archimède (IIIe siècle avant notre ère). Il est important que les appuis sur les côtés soient suffisamment lourds pour ne pas être déplacés par la poussée latérale exercée par le linteau.
Pour des ouvertures plus importantes, les architectes ajoutaient simplement des colonnes ou des caryatides, qui sont des colonnes sculptées en forme de femmes (la variante masculine se nommant Atlante), ce qui donne des édifices comme l’Érechthéion sur l’Acropole d’Athènes. Ces colonnes étaient alors surmontées de linteaux comme une porte.

La même idée fonctionne avec des voûtes en arc de cercle comme en construisaient les Romains, mais qu’on trouve déjà chez les Égyptiens et les Grecs, même si c’est dans des constructions utilitaires comme des entrepôts ou des canalisations. Ici encore, le poids de la voûte s’exerce sur les piliers latéraux dont la masse assure la stabilité de l’ensemble.

Ces voûtes peuvent être prolongées pour former le plafond d’une salle, elles servent aussi à construire des ponts comme les deux ponts d’Albi, le vieux datant de 1040 et le neuf de 1867.

Les dômes
Mis à part les toits plats ou en pentes et les voûtes, les Grecs eurent l’idée de toits hémisphériques, autrement dit de dômes. Le principe de la stabilité de ces structures repose sur des murs solides, calculés pour soutenir le dôme, comme pour les voûtes. Les dômes de l’Antiquité comme celui de Sainte Sophie à Constantinople (aujourd’hui Istanbul) ont des assises massives, qui permettent la stabilité du tout même si le dôme de Sainte Sophie s’écroula en 1346, suite à un séisme survenu deux ans plus tôt.

La cathédrale Santa Maria del Fiore de Florence posa un problème plus épineux. En 1418, la cathédrale était achevée mis à part un trou béant de 45 mètres de diamètre au-dessus d’un tambour octogonal de 53 mètres de haut. D’après les plans de l’architecte initial, décédé depuis longtemps, un dôme devait reposer sur ce tambour. L’ennui est que personne ne savait ni comment le faire tenir sur une structure aussi légère, ni comment le construire sans échafaudage en bois, comme on le faisait à l’époque mais impossible ici du fait de la trop grande portée. La question fut mise au concours et Filippo Brunelleschi (1377 – 1446) le remporta avec une double structure légère, une à l’extérieur, l’autre à l’intérieur. Finalement, le tout fut monté progressivement par anneaux horizontaux et sans échafaudage, un peu comme on le fait dans certains pays d’Afrique pour des cases en forme d’ogive. Ce type de construction semble venir de l’antique Nubie, car on en trouve en haute Égypte.