Jean-Henri Fabre est connu pour son observation des insectes. Excellent vulgarisateur, il est de ceux qui savent communiquer leurs passions. Les mathématiques en font partie.

Jean-Henri Fabre

Bien que titulaire d’une licence de mathématiques, d’un doctorat en sciences naturelles et de plusieurs autres diplômes, Jean-Henri Fabre est un autodidacte comme il le rappelle lui-même :

Apprendre sous la direction d’un maître m’a été refusé. J’aurais tort de m’en plaindre. L’étude solitaire a sa valeur ; elle ne vous coule pas dans un moule officiel, elle vous laisse votre pleine originalité. Le fruit sauvage, s’il arrive à maturité, a une autre saveur que le produit de serre chaude ; il laisse aux lèvres qui savent l’apprécier un mélange d’amertume et de douceur dont le mérite s’accroît par le contraste.

Son côté autodidacte le rend attachant pour certains et agaçant pour d’autres. Quelques modernes lui reprochent aussi de ne pas avoir épousé les thèses de Darwin qui, en revanche, reconnaissait en lui un observateur incomparable. Il s’explique lui-même dans une de ses lettres à Darwin :

Vous vous étonnez de mon peu de goût pour les théories, si séduisantes qu’elles soient. Ce travers d’esprit, si c’en est un, tient un peu à mes longues études mathématiques qui m’ont habitué à ne reconnaître la vérité qu’à la lueur d’un irrésistible faisceau de lumière. Ne jurant par aucun maître, libre d’idées préconçues, peu enclin aux séductions des théories, je cherche avec passion la vérité, près à l’admettre quelle qu’elle soit et de quelque fait qu’elle vienne. Et comme moyen de recherche, je ne connais qu’une chose : l’expérience.

Par ailleurs, Darwin l’avait chargé d’expériences sur les insectes retournant à leurs nids. Les résultats se trouvent dans l’œuvre de Fabre. De façon générale, on trouvera la plupart des écrits de Fabre sur internet.

Fabre créationniste ?

Parmi les critiques modernes faites à Jean-Henri Fabre, certains le stigmatisent comme créationniste car il ne croyait pas à la théorie de Darwin, qu’il comparait à celle de la génération spontanée. À la défense de Fabre, il faut noter que la théorie originelle de Darwin n’était pas celle qui porte son nom aujourd’hui. Il s’agissait plutôt d’une transposition de la sélection des espèces domestiques, pratiquée depuis longtemps par les éleveurs, en une sélection naturelle sous l’effet de modifications du milieu. Autrement dit, il lui manquait l’explication qui viendra avec la découverte des gênes, par Gregor Mendel au début du XX^e siècle. La théorie de l’évolution telle que nous la connaissons est postérieure de vingt ans à la mort de Fabre ! Comment peut-on lui reprocher de ne pas l’avoir reconnue ?

Mais l’essentiel n’est pas là, il est dans deux choses, sans parler de l’inélégance d’attaquer les morts, qui ne peuvent se défendre. Premièrement, il faut savoir ne pas se tromper d’adversaires. Les obscurantistes que sont les créationnistes ne sont pas les disciples de Jean-Henri Fabre. Ils sont dans des religions qui refusent la science, et malheureusement pas la violence. Deuxièmement, de Jean-Henri Fabre retenons plutôt l’exceptionnel talent de vulgarisateur. Pour finir sur une note poétique et liée à la question de l’évolution, voici l’un de ses commentaires sur la parade nuptiale des scorpions languedociens : La colombe a, dit-on, inventé le baiser. Je lui connais un précurseur : c’est le scorpion.

Jean-Henri Fabre a réussi à me faire regarder les scorpions autrement, c’est pourquoi je me souviens de cette remarque. Aujourd’hui, elle me fait m’interroger : selon la théorie créationniste, parler de précurseur d’une espèce a-t-il un sens ?

Descriptions et mathématiques chez Fabre

Dans ses souvenirs entomologiques, Jean-Henri Fabre dépeint les mœurs des insectes de manière vivante, en les ramenant souvent aux nôtres. Il décrit ainsi le carabe doré en nous emmenant d’abord visiter les abattoirs de Chicago pour comparer ensuite leur efficacité à celles des carabes dont on saisit mieux ainsi la férocité comme la voracité.

Il conclut alors sur nos origines et notre avenir, avec l’abolition de l’esclavage et l’instruction des femmes, les deux voies du progrès moral selon lui. Cette façon de généraliser sera parfois critiquée plus tard, comme peu scientifique. Il est vrai que, par moments, Fabre concluait un peu vite. Par exemple, voici comment il décrit la toile d’une araignée, l’épeire :

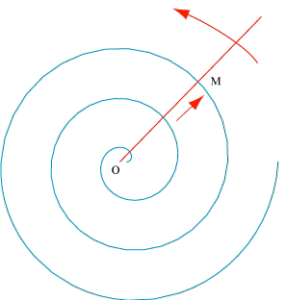
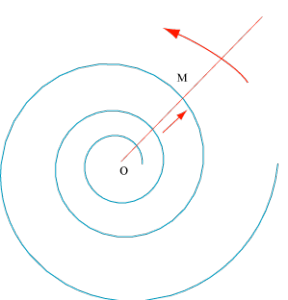
Nous reconnaîtrons d’abord que les rayons sont équidistants ; ils forment de l’un à l’autre des angles sensiblement égaux […] les divers tours de spire […] avec les deux rayons qui les limitent, forment d’un côté un angle obtus et de l’autre un angle aigu […] d’un secteur à l’autre, ces mêmes angles, l’obtus comme l’aigu, ne changent pas de valeur, autant que peuvent en juger les scrupules du regard seul.

Fabre reconnaît alors une propriété caractéristique de la spirale logarithmique et en conclut que la toile de l’épeire épouse cette forme, ce qui est rapide surtout quand la mesure a été faite à l’œil. Ceci dit, cela n’enlève rien à la qualité de son travail, et il n’en reste pas moins que, du fait de sa construction, la toile prend une forme de spirale.

De même, c’est de manière très mathématique qu’il explique la forme de poire que le scarabée sacré donne à la bouse dans laquelle il dépose son œuf : une sphère pour minimiser la surface externe afin de réduire la dessiccation, qui rendrait la bouse immangeable pour la larve, coiffée d’une sorte de cylindre contenant l’œuf, qui se trouve ainsi dans un endroit plus aéré.