Archives pour la catégorie Nature

Mathématiques, Nature, Philosophie, Regard sur le monde

Les mathématiciens sont-ils tous platoniciens ?

Laisser un commentaire

Comme Platon, les mathématiciens sont des créateurs de mondes, tels celui du mythe de la caverne. Doit-on pour autant considérer les mathématiciens comme platoniciens ?

Qu’elle fut ou non gravée à l’entrée de son académie, la phrase Que nul n’entre ici s’il n’est géomètre est conforme à la pensée de Platon : il est bon que le philosophe apprenne la géométrie. Au livre VII de La république, il mentionne d’ailleurs son étude comme un pré requis à celle de la philosophie, et une matière indispensable dans le cursus du futur citoyen. Les mathématiques forgent la pensée de Platon, comme on le voit dans Le Ménon. Inversement, tout mathématicien est-il platonicien ?

Un créateur de mythes

Avant d’essayer de répondre à cette question, examinons le mode de pensée de Platon. Sa méthode fondamentale est la création de mythes. Le procédé est classique dans l’Antiquité où l’usage de métaphores permettait d’introduire des concepts abstraits à travers des expériences quotidiennes. Le mythe le plus célèbre inventé par Platon est celui de la caverne, où il introduit le concept de « monde des idées ». En voici un résumé rapide. Des hommes, enfermés dans une caverne, ne voient l’extérieur qu’à travers des ombres. Ils n’ont pas accès à la réalité mais seulement à son image. Ce mythe est une métaphore où la caverne est notre monde, et l’extérieur, le monde des idées. Une transposition est nécessaire pour comprendre le message de Platon, même si celle-ci est claire.

Le monde des idées

Ce monde des idées, existe-t-il ? Platon l’a postulé, ce qui l’a mené à adopter la thèse de l’immortalité de l’âme. Elle lui permet d’affirmer qu’elle vient de ce monde et, pour cette raison, en garde une vague mémoire. La philosophie grecque a parfois ce côté jusqu’au boutiste, que l’on retrouve facilement chez les mathématiciens. Pas question pour eux que 2 + 2 fasse 3,99. C’est 4 sans discussion possible. Cette démarche, correcte quand elle reste dans son cadre, peut aboutir parfois à des extravagances inutiles, comme l’idée d’une âme immortelle, même dans le passé. Platon en avait besoin pour expliquer notre accès instinctif à son monde des idées. Pour lui, on n’apprend pas, on se souvient. Cette remarque explique la pédagogie de Socrate dans Le Ménon, quand il fait démontrer le théorème de Pythagore à un esclave. Celui-ci est censé retrouver des connaissances lointaines, du temps où son âme n’était pas prisonnière de son corps. Socrate aide son interlocuteur à « accoucher » de ce qui existe déjà en lui. Dans ce sens, l’invention est impossible, seul « trouver » l’est. Ce vocabulaire correspond à celui utilisé en général en mathématiques. L’expression « il invente des théorèmes » est souvent péjorative, car elle sous entend qu’ils sont faux.

Le monde des idées mathématiques

De même, les mathématiciens inventent des mondes, semblables au monde des idées de Platon. Aucun point du monde réel n’est jamais le point idéal que nous imaginons. Il a forcément une certaine épaisseur. Il en est de même de la droite et du cercle. Nous en avons des idées que nous visualisons et même matérialisons, mais c’est sur les idées que nous raisonnons. Pour rendre ses résultats plus solides, depuis l’Antiquité, le monde de la géométrie est régi par un certain nombre d’axiomes, c’est-à-dire de résultats considérés comme vrais sans démonstration. Cette méthode a été généralisée et approfondie par David Hilbert au début du XXe siècle. De nos jours, chaque théorie (arithmétique, géométrie, etc.) a ses axiomes, qui la structurent.

L’ombre des idées

Ces théories ont un rapport complexe avec la réalité. Officiellement, pour les mathématiciens, les axiomes résultent du libre arbitre des créateurs de ces théories. Est-il raisonnable de le prétendre, ou est-ce un moyen de se libérer de la réalité ? Restons dans le domaine de la géométrie pour donner un exemple. On y démontre une propriété de la parabole, liée à son foyer (appelée propriété focale pour cela), que nous résumons par un dessin.

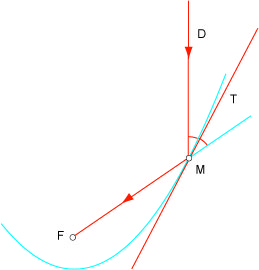
Propriété focale de la parabole : Si une droite D parallèle à l’axe d’une parabole coupe celle-ci en un point M, la droite symétrique de D par rapport à la tangente en M à la parabole passe par son foyer.

Cette propriété a des conséquences visibles dans notre univers quotidien : paraboles sur les toits des immeubles, fours solaires petits et grands, phares des voitures ou des bords de mer. La propriété des paraboles existant dans le monde de la géométrie s’applique dans notre monde.

Parabole en montagne. L’utilisation d’un miroir en forme de parabole permet de focaliser les rayons du soleil en un point et donc de faire bouillir de l’eau. © Hervé Lehning

Peu de mathématiciens doutent réellement de cette efficacité, même si certains scientifiques l’estiment « déraisonnable ».

Vérité des axiomes

La raison de cette « estimation » est l’opinion exprimée par les mathématiciens contemporains eux-mêmes. Si vous les questionnez sur ce que sont les axiomes, il est probable qu’ils répondront comme nous l’avons exposé plus haut. Ce sont des règles que l’on se donne de manière arbitraire, et sur lesquelles on développe une théorie cohérente, en suivant les règles de la logique. De ce point de vue, cette théorie n’est pas plus « réelle » ou « vraie » que les axiomes qui la fondent. Cependant, les résultats acquis sont extrêmement solides. Si on admet la « vérité » des axiomes, celle des théorèmes suit.

Les théories mathématiques : des modèles

Si cette vérité est conditionnelle, pourquoi les résultats des mathématiques sont-ils utiles dans le monde réel ? La réponse est simple. Les axiomes ne sont pas choisis arbitrairement ! Plutôt que de le prétendre, il serait préférable de dire que, s’ils l’étaient, on pourrait encore parler de mathématiques. Mais ils ne le sont pas ! Le fait est que l’on ne s’intéresse pas à ces mathématiques du bon plaisir. Ils sont choisis pour que les théories mathématiques qui en découlent soient de bons modèles de la réalité. Pour cela, ils s’en inspirent. Comme Platon, les mathématiciens inventent des mondes idéaux, dont la réalité est un reflet. En ce sens, ils sont platoniciens mais des platoniciens rarement dupes de leurs modèles. Ils ont conscience que leur monde des idées est une abstraction dont ils sont l’origine. Ce n’est pas un monde préexistant de toute éternité, comme le monde des idées de Platon.

Ecologie, Mathématiques, Nature, Photographies, Regard sur le monde, Voyages

Des plantes et des maths

Un commentaire

Les plantes ont un rapport étonnant avec les mathématiques, hasard ou nécessité ? Je vous laisse juger.

Suite de Fibonacci

Léonard de Pise, dit Fibonacci, a créé sa suite comme un simple exercice d’arithmétique :

Un homme met un couple de lapins dans un lieu isolé de tous les côtés par un mur. Combien de couples obtient-on en un an si chaque couple engendre tous les mois un nouveau couple à compter du troisième mois de son existence ? 

Le calcul est simple, la suite donne : 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, etc. Chaque nombre est la somme des deux qui le précèdent.Cette règle a fasciné au-delà de l’exercice. De plus, on la retrouve souvent dans la nature. En voici quelques exemples.

1, 2, 3, fleurs dans le désert du Namib (Namibie).                     © Hervé Lehning

Cette suite se retrouve plus souvent dans le décompte des pétales des fleurs. La seule façon de les compter est malheureusement de les effeuiller …

Saurez-vous trouver le nombre de Fibonacci derrière ces pétales de griffes de sorcière (littoral du sud de la France) ? © Hervé Lehning

La géométrie, des rosaces à la sphère

Après l’arithmétique, nous trouvons la géométrie avec des rotations surprenantes et des développements en sphère.

Rotation naturelle dans une plante succulente. La règle de formation des feuilles implique que celles-ci se déduisent l’une de l’autre par rotation. Littoral du sud de la France.     © Hervé Lehning
Cette plante sauvage des Alpes se développe naturellement en sphère. Parc des Écrins                © Hervé Lehning

Intersection d’un cercle et d’une droite dans la toundra

Cercle et droite sur une plante de la toundra. Groenland      © Hervé Lehning

Cette plante de la toundra groenlandaise présente deux formes géométriques simples : un cercle et une droite. Le cercle est naturel. Il correspond au développement de la plante dans toutes les directions à partir d’une graine, mais pourquoi a-t-elle dépéri d’un seul côté d’une droite ?

Ecologie, Mathématiques, Nature

Un lemming ne se suicide jamais !

Laisser un commentaire

Selon la légende, le lemming – un petit rongeur ressemblant à un hamster, vivant dans les régions nordiques comme la Suède, le Canada et le Groenland – est d’un altruisme tel qu’il se suicide en masse pour le bien de sa communauté quand celle-ci devient trop nombreuse. Même si l’idée de suicides d’animaux est étonnante, l’évolution de la population lemming suit effectivement une courbe étrange.

Évolution de la population de lemmings, on note un cycle de quatre ans. Le rapport entre les minima et maxima est de 1 à 1000, ce qui peut faire penser à une extinction des lemmings.

Un film “documentaire”

Cette courbe se recopie elle-même tous les quatre ans mais, quand la population lemming est à son minimum, on peut penser à une extinction car le rapport entre minimum et maximum est de 1 à 1000 environ. En fait, il n’en est rien et ils reviennent toujours avec une périodicité de quatre ans, et ceci dans toutes les contrées où ils vivent. En 1958, dans White Wilderness, les studios Walt Disney ont présenté des vagues de lemmings se précipitant dans la mer du haut d’une falaise. Bien entendu, il s’agissait d’un trucage cinématographique. Un examen attentif du film montre d’ailleurs que l’on ne voit jamais plus de 12 lemmings simultanément à l’écran. S’il n’en est pas à l’origine, ce film « documentaire » a sans doute conforté la fable selon laquelle le lemming se suicide en masse quand la population de sa communauté devient trop importante pour la région où il habite.

Un modèle mathématique

Un labbe en train de dévorer un bébé manchot. @ Hervé Lehning

En fait, ces fluctuations peuvent s’expliquer par la présence d’un prédateur exclusivement dévoué au lemming, l’hermine. Ce petit rongeur en a d’autres, comme les renards, les labbes et les harfangs, mais ceux-ci mangent ce qu’ils trouvent le plus facilement alors que l’hermine ne chasse que le lemming. Elle provoque ainsi sa quasi extinction … et donc la sienne en conséquence, ce qui laisse aux survivants la chance de reconstituer le peuple lemming et à l’histoire de recommencer éternellement. Cette façon, somme toute littéraire, de présenter le phénomène permet de comprendre son côté qualitatif. Un modèle mathématique précise son côté quantitatif. Nous en proposons une version très rudimentaire, car il ne tient pas compte des saisons, même s’il suffit cependant à vérifier le phénomène.

Une hermine.

Admettons qu’en l’absence de prédateurs, la population des lemmings croisse hebdomadairement avec un taux dépendant de la natalité et de la mortalité naturelles. La présence de l’hermine change la donne, et ce taux doit être minoré d’une valeur proportionnelle au nombre d’hermines. Autrement dit, un nouveau coefficient rentre en jeu, qui correspond à la prédation. Pour fixer les idées, si le taux de croissance naturelle des lemmings est égal à 1,05 et le taux de prédation égal à 0,0001, une population de 1000 hermines donne un taux de croissance de la population lemming égal à son taux naturel 1,05 moins la prédation, soit 0,0001 multiplié par 1000. Le taux total est donc égal à 1,04. Si la population lemming est de 40000 individus, elle est de 40000 multiplié par 1,04 la semaine suivante, soit 41600 individus.

Pendant ce temps, la population d’hermines évolue aussi du fait de son taux de croissance naturel qui doit être majoré d’une valeur proportionnelle au nombre de lemmings. Si le taux de croissance naturel est de 0,97 et le taux dû à l’alimentation (c’est-à-dire à la prédation) est de 0,000001, le taux de croissance des hermines est de 0,97 plus 40000 multiplié par 0,000001, soit 1,01. La population d’hermines la semaine suivante est donc égale à 1000 multiplié par 1,01 soit 1010.

Gestion des animaux dans les parcs naturels

Les mêmes calculs peuvent être repris la semaine suivante et les quatre paramètres ajustés pour correspondre à la réalité constatée sur le terrain, ce que nous avons fait d’ailleurs. Les valeurs ci-dessus donnent bien une périodicité de quatre années environ. Ces formules sont générales et valables pour d’autres couples proies / prédateurs. Elles servent pour la gestion des animaux dans les parcs naturels. Par exemple, si on constate un risque de fort accroissement du nombre de prédateurs, la direction du parc peut décider d’autoriser la chasse d’un certain nombre d’animaux pour éviter un cycle d’évolution des populations chaotique.

Ecologie, Mathématiques, Nature, Réflexions

L’effet papillon d’Edward Lorenz

Laisser un commentaire

L’effet papillon est un exemple très rare d’expression venant des mathématiques ayant eu un succès médiatique incontestable. Tout le monde connaît l’effet papillon : petites causes, grandes conséquences comme certains l’ont chanté.

L’origine de la métaphore

En 1972, à une conférence de météorologie, Edward Lorenz a présenté un exposé sous un titre qui a frappé les esprits :

Le battement d’ailes d’un papillon au Brésil peut-il provoquer une tornade au Texas ?

Cette métaphore n’est toutefois pas de Lorenz mais d’un organisateur de la conférence, Philip Merilees. Pour justifier sa question, Lorenz utilisait un modèle mathématique très simplifié de l’atmosphère terrestre où il n’avait conservé que trois inconnues pouvant donc être représentées par un point de l’espace. Il s’agit de ce qu’on appelle en mathématiques un système dynamique. On part d’une condition initiale, c’est-à-dire d’un point représentant l’état du système à l’instant initial et le modèle nous donne les états du système aux instants qui suivent, théoriquement indéfiniment.

L’attracteur de Lorenz

Dans le cas du modèle de Lorenz, chaque condition initiale donne une orbite ressemblant grossièrement aux deux ailes d’un papillon. De plus, toutes les orbites s’agglutinent sur un même objet également en forme de papillon, qu’on nomme l’attracteur de Lorenz.

L’attracteur de Lorenz a une forme de papillon. © Hervé Lehning

Cette forme explique peut-être le choix de cet insecte par Merilees. Peu importe, le papillon a séduit bien au-delà de la sphère mathématique sans que, pour autant, le message de Lorenz soit complètement compris. En effet s’il mettait l’accent sur la sensibilité aux conditions initiales, un faible changement pouvant avoir de grosses conséquences, il corrigeait immédiatement l’idée de la soumission au hasard d’un battement d’aile de papillon par :

J’avance l’idée qu’au fil des années de petites perturbations ne modifient pas la fréquence d’apparition d’événements comme les tornades : la seule chose qu’ils peuvent faire, c’est de modifier l’ordre dans lequel ces événements se produisent.

Nous sommes ainsi très loin de la notion couramment vulgarisée : petites causes, grandes conséquences. Dans la pensée de Lorenz, le chaos sert à la prévision, les orbites ne sont pas aléatoires, elles se situent sur l’une ou l’autre aile de l’attracteur, le passage de l’une à l’autre semblant aléatoire. Cette conception éclaire l’idée a priori paradoxale qu’on puisse étudier l’évolution du climat sans pour autant être capable de prévoir le temps du mois suivant.

Nature, Photographies

Rencontre en descendant du Pelvoux

Laisser un commentaire
Chamois surpris en descendant du Pelvoux © Hervé Lehning

 

Sur les sentiers de montagne, on rencontre souvent des promeneurs armés de jumelles essayant de distinguer quelques chamois au loin, sur les sommets. Nul ne semble espérer voir un chamois de très près.

L’art de surprendre un chamois

C’est cependant plutôt facile en tenant compte de plusieurs caractéristiques de cet animal. Premièrement, même si sa vue n’est pas si mauvaise quand il s’agit de repérer un animal en mouvement, il distincte mal un objet immobile. Par exemple, le jeune chamois sur la photo ci-dessus se doute visiblement de ma présence mais n’arrive pas à me distinguer car je me suis immobilisé, même si je me tiens debout à une dizaine de mètres de lui. J’ai pu m’approcher d’aussi près car je me suis déplacé contre le vent pour qu’il ne me sente pas, de plus le vacarme d’un torrent en contrebas ne lui a pas permis pas de m’entendre. Deux personnes bruyantes arrivant de l’autre côté l’ont fait s’enfuir quelques minutes plus tard. Elles ont été étonnées d’apprendre qu’un chamois broutait tranquillement quelques instants plus tôt au lieu même où elles se trouvaient.

Ecologie, Nature, Réflexions, Regard sur le monde

Réflexions sur les fins du monde

Laisser un commentaire

La Terre a déjà connu plusieurs fins du monde, plus précisément cinq extinctions de masse. Les géologues l’ont découvert au XVIIIe siècle en étudiant les couches de sédiments empilées sous nos pieds, cinq ne contiennent quasiment aucune trace de vie. La plus médiatique de toutes les extinctions de masse est la dernière en date, celle qui a vu disparaître les dinosaures voici 65 millions d’années.

Un dinosaure © The Field Museum

La fin catastrophique des dinosaures

Depuis les années 1970, cette fin du monde des dinosaures est souvent expliquée par une catastrophe. Par un malheureux hasard, la trajectoire de notre planète aurait rencontré celle d’un astéroïde de 10 kilomètres de diamètre. Événement peu probable mais qui s’est effectivement produit aux environs de cette époque, à Chicxulub au Mexique. Telle une bombe thermonucléaire, cet astéroïde a projeté un immense nuage de poussière dans l’atmosphère, voilant le soleil et créant une espèce d’hiver nucléaire. Les dinosaures seraient donc morts de ce que redoutaient les hommes au temps de la guerre froide. L’idée qu’ils auraient disparu à la suite de l’impact d’un astéroïde est d’ailleurs due à un physicien nucléaire américain, Luis Walter Alvarez (1911 – 1988), prix Nobel de physique en 1968, qui participa à la mise au point des détonateurs de la bombe atomique au plutonium et qui avait donc réfléchi aux conséquences que pouvaient avoir l’usage de cette arme. Plus profondément, il est intéressant de constater que l’imaginaire de chaque époque se projette sur ses explications, scientifiques ou autres.

Mis à part ce fait troublant, il est permis de se demander pourquoi les petites bêtes ont survécu. Pourquoi les extinctions sont-elles aussi sélectives ? C’est le point le plus gênant de cette théorie des catastrophes. De plus, l’explication, qui n’est pas valable pour les autres extinctions dont celle, plus importante, de la fin du Permien (voici 500 millions d’années), est-elle valable pour celle des dinosaures ? Il est permis d’en douter depuis que certaines études montrent que l’impact de l’astéroïde incriminé serait antérieur de 300 mille ans à leur disparition. Une bien longue survie pour une agonie !

La fin par le changement de milieu

À cette explication des extinctions par le hasard, d’autres paléontologues ont préféré avancer un modèle probabiliste tenant compte du métabolisme des animaux. Pour donner un exemple, quelle serait l’influence d’une baisse de la proportion de l’oxygène dans l’air ? Certains animaux s’adapteraient très bien, d’autres non. Sans doute pourrait-on établir une corrélation entre la concentration en oxygène et la probabilité de survie d’une espèce donnée. Cette corrélation serait fonction du métabolisme et expliquerait facilement aussi bien les disparitions que les survies. Rassurez-vous, l’homme est très compétitif dans ce domaine ! Nous nous adaptons très bien à la raréfaction de l’oxygène.

De façon moins évidente, il en est de même du calcium. Les animaux à squelette important en dépendent de manière cruciale. Les dinosaures en faisaient partie. On dénombre sept facteurs favorables à la bio-minéralisation du calcium : ions calcium Ca2+ sursaturés, température chaude et tropicale, bas niveau de dioxyde de carbone CO2, calme volcanique (et orogénique), pH neutre ou alcalin, niveau d’oxygène favorable, chaîne alimentaire intacte. Bien entendu, les facteurs opposés sont perturbateurs de la bio-minéralisation du calcium. Un compte des facteurs positifs et négatifs permet d’estimer la probabilité de bio-minéralisation du calcium. Si elle est faible, la survie de certaines espèces devient difficile. Certains paléontologues en ont déduit un modèle probabiliste : les facteurs perturbateurs de la bio-minéralisation du calcium seraient les causes des extinctions de masse. Pour simplifier, disons que plus on compte de facteurs perturbateurs, plus on risque une extinction massive et plus celle-ci est importante.

Voyons ce modèle à l’œuvre pour les dinosaures. Pour eux, on dénombre cinq facteurs perturbateurs : glaciations, niveau élevé de CO2, activité orogénique et volcanique intense, augmentation de l’acidité du pH, rupture des chaînes alimentaires (au niveau des planctons). On a donc ici un score de 5 sur 7 ! Pour l’extinction du Permien, c’est pire : 6 sur 7 ! Pour les autres extinctions de masse, les scores varient entre 2 et 3 sur 7. Chaque fois, le score est proportionnel à l’importance de l’extinction.

La sixième extinction

Pour certains chercheurs, la sixième extinction massive a commencé voici cent mille ans. Pourquoi ? Ils constatent d’abord qu’une espèce de mammifères et une espèce d’oiseaux disparaissent chaque année, ensuite que la durée moyenne de vie des espèces fossiles est de l’ordre du million d’années. Il existe actuellement 5000 espèces de mammifères et 10000 d’oiseaux. S’il n’y avait pas extinction, la moyenne annuelle de disparition devrait donc être mille fois plus faible que celle constatée ! Retrouve-t-on l’extinction actuelle dans le modèle probabiliste ? Bien entendu, oui, à cause de l’effet de serre qui est lié au CO2 !

À chaque époque sa fin du monde ?

Les extinctions de masse seraient donc dues, en particulier, à l’effet de serre. Le seul doute que nous puissions formuler contre ce modèle probabiliste est notre remarque précédente sur la disparition des dinosaures. Chaque époque retrouve ses problèmes dans le passé. Chacune a la fin du monde qu’elle redoute, bombe atomique ou effet de serre pour ne citer que les dernières. Le hasard, qui est le moteur de l’évolution, peut cependant nous réserver bien d’autres surprises. L’expérience montre que les fins du monde restent cependant des événements rares : cinq en plus d’un milliard d’années alors que la sixième fin du monde, celle qui pourrait nous concerner, a été annoncée plusieurs centaines de fois.