Par les idées qu’elle mobilise, la démonstration du théorème de la médiane est plus intéressante que le résultat lui-même. C’est cependant naturellement que nous commencerons par l’énoncer.
Enoncé
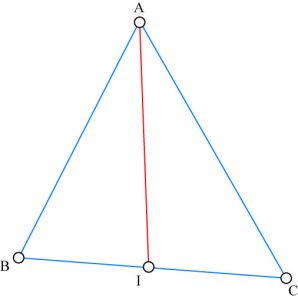
On considère un triangle ABC, I le milieu du côté BC. AI est donc une médiane du triangle. La formule suivante permet de calculer sa longueur :
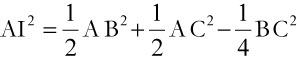
Démonstration
Une idée simple pour démontrer ce théorème est d’utiliser la notion de vecteur car :
![]()
En utilisant la notion de produit scalaire, on obtient :
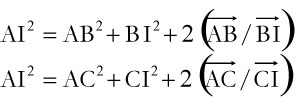
En faisant la somme et en utilisant la relation :
![]()
On obtient :
![]()
Comme :
![]()
On en déduit le résultat.

ce n’est pas (AB / BI) mais AB . Bi (produit scalaire…) idem pour AC / CI
Question de notation, f scalaire g se note (f / g) en général, f.g évoquant plutôt le produit usuel.
J ai toujours noté par . le produit scalaire
Notons que ce n est pas une multiplication de vecteurs ! mais une notation qui permet à un couple de vecteurs d associer un nb réel
C’est bien pour cela qu’on dit “produit SCALAIRE”. Si on associe un vecteur, on parle de “produit VECTORIEL”.
pythagore et son thé au harem, ;o) ne sont-ils pas plus simple ?
vu que l’on connait deux cotés du triangle.
AI = rac(AB²-1/2BC²)
mais sans doute que là n’est toutefois pas la question…