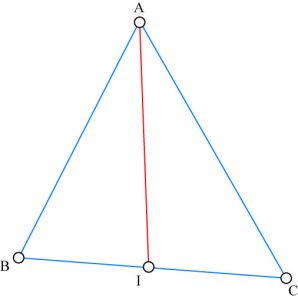
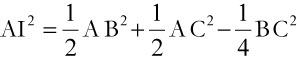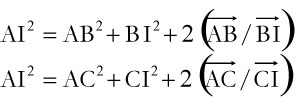Dans la vie courante, nous avons rarement besoin d’aller au-delà des mille milliards qui, forcément, font penser aux mille milliards de mille sabords du capitaine Haddock, le célèbre compagnon de Tintin.

Nicolas Chuquet (1445 – 1500) inventa pourtant un système pouvant aller bien au-delà. Dans son livre Triparty en la science des nombres, il forgea de nouveaux noms de nombres sur des préfixes correspondants à deux, trois,…, neuf : billion, trillion, quatrillion, quintillion, sextillion, septillion, octillion, nonillion. Le premier (un billion) est un million de millions, chacun est ensuite égal à un million de fois le précédent. Ce système est appliqué en Europe sauf dans les pays de langue anglaise car, malheureusement, les États-Unis ont adopté un système différent où chaque quantité est égale à mille fois la précédente. Ainsi, un billion américain vaut mille millions français donc à un milliard et ainsi de suite. D’autre part, on utilise aussi des préfixes comme déca, hecto, kilo, méga, etc. (voir le tableau système de noms des grands nombres). Ainsi, un kilogramme vaut 1000 grammes, etc. Les premiers ont un sens qui vient du grec où déka signifie dix, ékaton, d’où viennent les hécatombes, cent, kilo, mille, mégas, d’où vient mégalomane, grand, gigas, d’où vient gigantesque, géant, téras d’où vient la tératologie, monstre. Les autres donnent, toujours en grec, la puissance de 1000 utilisée. Ainsi péta vient de penté, qui signifie 5 et qui a donné pentagone, mais pas Pétaouchnock qui, bien qu’imaginaire est censée être une ville très éloignée, quelque part au fin fond de la Sibérie. Exa vient de hexa, qui signifie 6 et qui a donné hexagone. Les derniers sont là pour 7 (zetta) et 8 (yotta) mais sont artificiels.
| Nom français | Nom américain | Préfixe | Symbole | Valeur |
| dix | déca | da | 10 | |
| cent | hecto | h | 100 | |
| mille | kilo | k | 1000 | |
| million | méga | M | 1 000 000 | |
| milliard | billion | giga | G | 1 000 000 000 |
| billion | trillion | téra | T | 1 000 000 000 000 |
| billiard | quadrillon | péta | P | 1 000 000 000 000 000 |
| trillion | quintillion | exa | E | 1 000 000 000 000 000 000 |
| trilliard | sextillion | zetta | Z | 1 000 000 000 000 000 000 000 |
| quadrillon | septillion | yotta | Y | 1 000 000 000 000 000 000 000 000 |
Le système de noms des grands nombres va au-delà mais les nombres deviennent alors sans véritable utilisation concrète. On peut alors simplifier les mille milliards de mille sabords du capitaine Haddock en un seul péta sabord… mais ce serait moins musical et pourrait être mal interprété.
Les financiers utilisent parfois des expressions telles que kiloeuros (k€) ou millions d’euros (M€), qu’ils seraient plus logique de nommer mégaeuros vu le symbole M utilisé, mais cela n’apparaît pas normalement dans les comptes bancaires des particuliers. Sauf en période d’hyper inflation, comme en Allemagne en 1923 où on imprima des billets de 500 millions de marks, ou au Zimbabwe en 2009 où on alla jusqu’à 100 000 milliards, soit 100 trillions au sens anglo-saxon (voir la photographie un billet sans valeur), les particuliers n’ont pas besoin d’envisager des sommes supérieures au milliard français, donc au billion américain… et les États, guère plus.

En informatique, l’usage du système binaire fait que les préfixes ont un sens légèrement différent. Kilo signifie alors 1024 car ce nombre est égal à 2 à la puissance 10, méga vaut 1024 kilo, giga, 1024 méga, téra, 1024 giga et péta, 1024 téra, etc.
Les petits nombres
Pris à l’envers, ce système permet également de visiter l’infiniment petit (voir le tableau système de noms des petits nombres). Ici encore, les préfixes ont un sens. Les premiers viennent du grec où micro signifie petit et nano, nain. On passe ensuite à l’italien où piccolo, qui signifie petit, a donné pico. Les autres sont artificiels.
| Nom français | Nom américain | Préfixe | Symbole | Valeur |
| dixième | déci | d | 0,1 | |
| centième | centi | c | 0,01 | |
| millième | milli | m | 0,001 | |
| millionième | micro | m | 0,000 001 | |
| milliardième | billionième | nano | n | 0,000 000 001 |
| billionième | trillionième | pico | p | 0,000 000 000 001 |
| billiardième | quadrillonième | femto | f | 0,000 000 000 000 001 |
| trillionième | quintillionième | atto | a | 0,000 000 000 000 000 001 |
| trilliardième | sextillionième | zepto | z | 0,000 000 000 000 000 000 001 |
| quadrillonième | septillionième | yocto | y | 0,000 000 000 000 000 000 000 001 |
Système de noms des petits nombres. Le système va au-delà mais les nombres deviennent alors sans véritable utilisation concrète.