La notion d’enveloppe de droites recouvre deux notions en général équivalentes. D’un côté, il s’agit d’une courbe séparant deux domaines entre eux, de l’autre une courbe tangente à toutes les droites. La seconde se prête mieux au calcul.
Exemple d’une porte d’autobus
Prenons un exemple concret, celui d’une porte d’autobus coulissante à deux battants s’ouvrant selon le schéma :

La projection sur le sol de la porte de droite (sur la figure) est un segment qui définit une droite coupant deux droites perpendiculaires selon un segment AB de longueur constante (celle de la porte entière).

Apparition d’une enveloppe
Il est facile de tracer un grand nombre de segments AB en faisant varier l’angle t de 0 à 90° on voit alors apparaître une courbe en négatif : leur enveloppe.
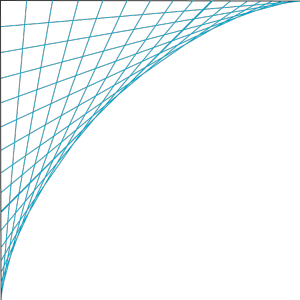
Si on fait varier l’angle t de 0 à 360°, on obtient une courbe en forme d’astre, appelée pour cela astroïde.
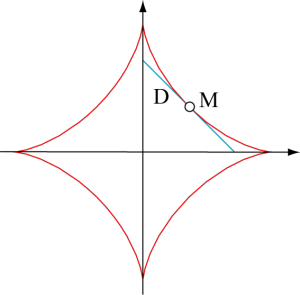
Point de Monge
Gaspard Monge (1746 – 1818), l’un des créateurs de l’école polytechnique et de l’école normale supérieure où il a ensuite enseigné a trouvé un moyen de décrire l’enveloppe d’une famille de droites dépendant d’un paramètre D (t) comme le lieu d’un point mobile, appelé depuis point de Monge en son hommage, ou simplement point caractéristique de D (t). Il se définit comme la limite du point d’intersection de D (t) et D (t + dt) quand dt tend vers zéro, ce qui permet son calcul à travers la notion de dérivée : le point de Monge est à l’intersection de D (t) et D’ (t) qui s’obtient en dérivant l’équation de D (t) par rapport à t.
Pour les férus de calculs, si a est le longueur de la porte, l’équation de D (t) est x sin t + y cos t = a cos t sin t donc les coordonnées du point de Monge est solution du système :
![]()
On en déduit ses coordonnées :
![]()
ce qui permet de tracer l’enveloppe de la famille de droites D.
