Suite du billet précédent L’univers holographique (1) : le paradoxe de l’information
Le paradoxe de l’information lié aux trous noirs reflète notre incapacité actuelle à élaborer une théorie cohérente de la gravité quantique. L’approximation semi-classique de Hawking cesse d’être valide quand le trou noir devient suffisamment petit pour que le rayon de courbure à l’horizon des événements atteigne la longueur de Planck, 10-33 cm, autrement dit lorsque non seulement la matière et l’énergie, mais aussi le champ gravitationnel doivent être quantifiés. La description finale de l’évaporation et la restitution partielle ou complète de l’information exigent donc un traitement complet en gravité quantique, branche fondamentale de la physique qui cherche à décrire la gravitation en utilisant les principes de la mécanique quantique.

L’application de la mécanique quantique aux objets physiques tels que le champ électromagnétique, qui s’étendent dans l’espace et le temps, a connu un succès éclatant avec la théorie quantique des champs[1]. Celle-ci forme la base de la compréhension du modèle standard de la physique des particules élémentaires, rendant compte des interactions électromagnétiques, nucléaire forte et nucléaire faible. Elle permet de calculer les probabilités d’événements en utilisant les techniques de la théorie des perturbations. Les diagrammes de Feynman décrivent les chemins de particules ponctuelles et leurs interactions. Chaque diagramme représente une contribution à un processus d’interaction. Pour leurs calculs, les physiciens additionnent en premier lieu les contributions les plus fortes, puis les plus petites, et ainsi de suite, jusqu’à atteindre la précision désirée.
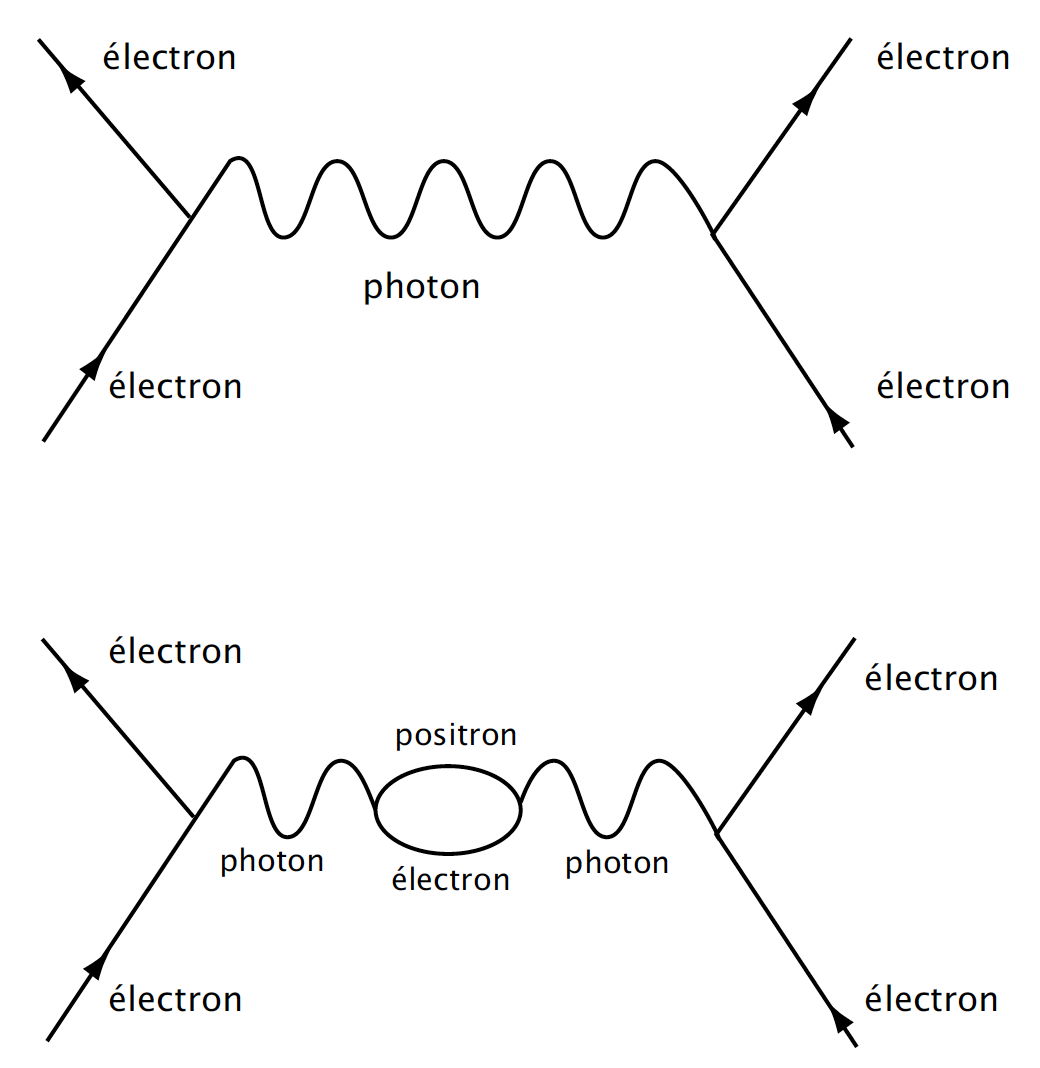
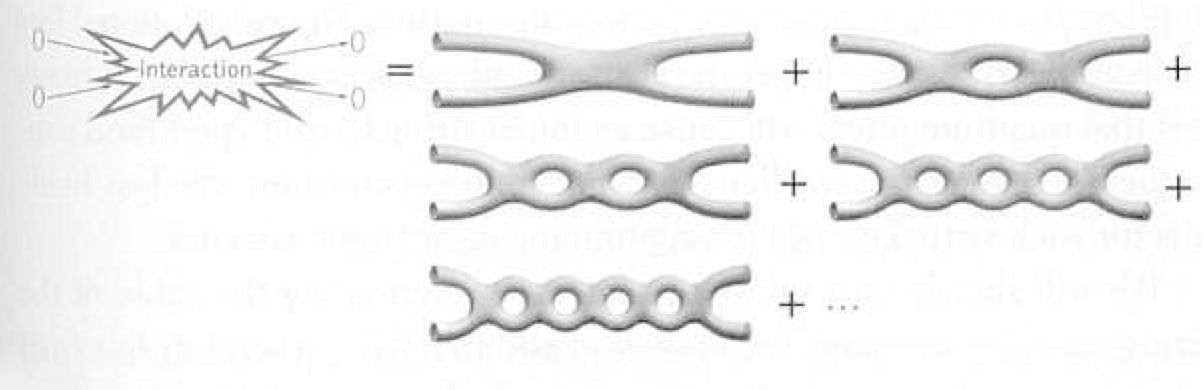
Mais ce procédé ne marche que si les contributions deviennent réellement négligeables à mesure qu’un plus grand nombre d’interactions est pris en compte. Lorsqu’il en va ainsi, la théorie est dite “faiblement couplée” et les calculs convergent vers des valeurs physiques finies. S’il en va différemment, la théorie est dite “fortement couplée” et les méthodes standard de la physique des particules échouent. C’est notamment ce qui arrive avec le graviton, supposé être la particule médiatrice du champ gravitationnel. Le graviton, créant de la masse-énergie, interagit avec lui-même, ce qui crée de nouveaux gravitons, qui à leur tour interagissent, et ainsi de suite, jusqu’à la divergence. L’échec de la technique des perturbations pour quantifier la gravité a donc conduit les physiciens à explorer d’autres voies.
Jusqu’à présent, la théorie de gravité quantique la plus étudiée est la théorie des cordes[2], même si d’autres approches comme la Loop Quantum Gravity[3] ou la géométrie non-commutative[4] offrent de prometteuses alternatives. L’idée de départ de la théorie des cordes est que les constituants fondamentaux de la matière (les quarks, les leptons et les bosons) ne sont pas des particules ponctuelles sans dimension, mais des objets longilignes et vibrants de dimension 1. Ces « cordes », de taille extrêmement petite, peuvent avoir deux formes : ouvertes aux extrémités libres, ou fermées en anneau. Leurs modes de vibration et d’enroulement sont quantifiés, et peuvent être associés à des particules de masse et de spin donnés.
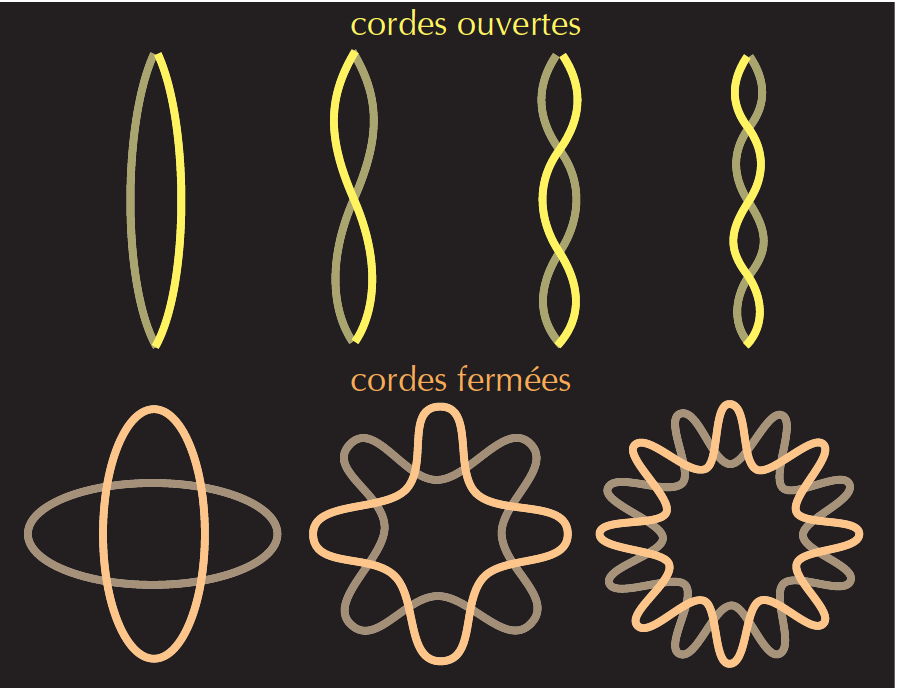
Une corde correspond ainsi à une variété infinie de particules. Les interactions entre particules sont décrites en termes de jonction et de scission de cordes. Les avantages de cette formulation sont évidents. D’une part, c’est la fin du « zoo des particules », puisque toutes les particules élémentaires se réduisent à deux familles, les cordes fermées et les cordes ouvertes ; d’autre part, les cordes admettent une échelle spatiale minimale et permettent d’éviter l’apparition de singularités, qui sont inévitables dans les théories quantiques des champs fortement couplées.
Mais il y a un prix à payer pour assurer la cohérence mathématique de la description : il faut supposer que l’espace-temps, décrit d’ordinaire à l’aide de quatre dimensions (trois d’espace, une de temps), acquiert six dimensions spatiales supplémentaires. Dans les années 1920, Theodor Kaluza et Oscar Klein avaient déjà tenté d’unifier l’électromagnétisme de Maxwell avec la gravitation d’Einstein en introduisant une cinquième dimension spatiale, enroulée sur elle-même. La tentative avait échoué, mais l’idée a été reprise et généralisée dans les années 1980 pour les besoins de la théorie des cordes [5]. En outre, l’intégration de la supersymétrie[6] dans la théorie des cordes peut se faire de cinq manières différentes. Dans certaines, toutes les cordes sont obligatoirement fermées sur elles-mêmes, formant des boucles ; dans une autre, les cordes sont ouvertes et leurs extrémités sont libres. La théorie des cordes supersymétriques s’est donc scindée en cinq théories dites des supercordes, aucune ne décrivant totalement la réalité.
Enfin, au début des années 1990, les théoriciens notèrent certaines relations entre les cinq théories de supercordes, appelées dualités. Au sens le plus général du terme, une dualité est une relation qui identifie deux théories. On peut imaginer une dualité comme un type particulier d’unification: dans une unification normale, on fusionne deux théories en une théorie plus large qui contient les deux précédentes à une certaine limite. Si on relie deux théories par une dualité, on démontre que les théories sont les mêmes ; elles n’apparaissent distinctes qu’en fonction du regard que l’on porte sur elles. Moyennant quoi les physiciens des cordes firent l’hypothèse que chacune des 5 théories était un cas particulier d’une méta-théorie, baptisée « théorie M » et fonctionnant cette fois dans un espace-temps à onze dimensions[7].

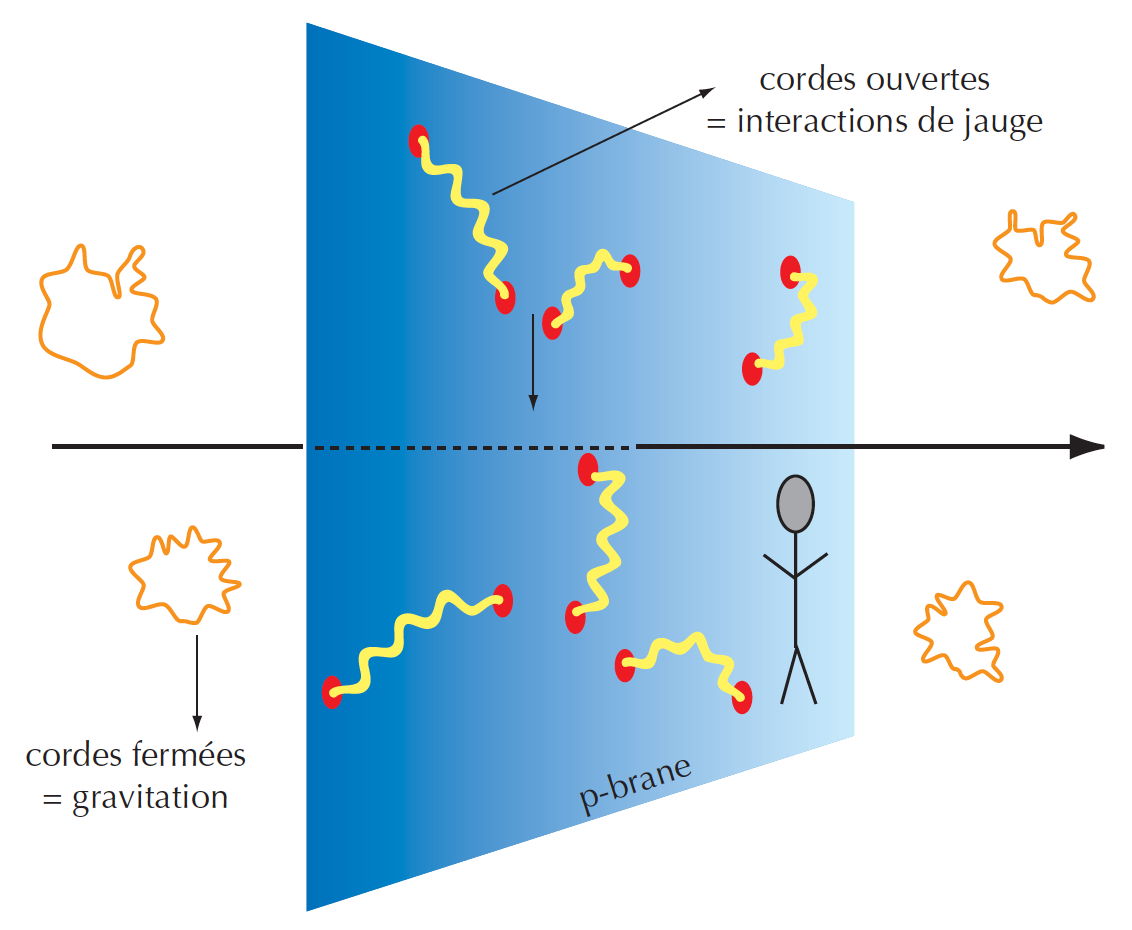
Les dimensions spatiales supplémentaires de la théorie M engendrent de nouveaux objets fondamentaux qui, par analogie avec les membranes qui enveloppent le tissu de l’espace-temps, sont appelés « p-branes », p étant un entier indiquant le nombre de dimensions spatiales de l’objet en question. Les cordes peuvent être vues comme des 1-branes, et notre espace tridimensionnel habituel comme une 3-brane – raison pour laquelle la théorie des cordes est parfois appelée « théorie des branes »[8]. Le système de branes forme donc un espace-temps multidimensionnel, la « matrice » (bulk), les cordes ouvertes ont leurs extrémités s’appuyant sur des 3-branes, tandis que les cordes fermées (représentant les gravitons) vivent dans les autres dimensions.
Notons que ces concepts très techniques et abstraits évoquent des images de réalité virtuelle et l’idée que nous vivrions dans une Matrice, ce qui, en dehors de Hollywood, ne saurait être plus éloigné de la réalité… [9].
Pour clore ce bref rappel historique, précisons que la théorie des cordes et la théorie M sont toujours en chantier. Nous disposons d’équations approximatives pour les cordes et les branes, mais nous en ignorons les équations exactes. Nous ignorons aussi comment calculer à partir des équations des cordes d’innombrables quantités physiques. Mais nous savons qu’en régime de couplage fort, les branes courbent suffisamment l’espace-temps pour engendrer des « branes noires », généralisation des trous noirs de la relativité générale classique. Raison pour laquelle dans les années 1990, on a pu réaborder la question du paradoxe de l’information dans le cadre de la gravité quantique des cordes.
En complément, voici une brève vidéo où je résume très succinctement le statut de la théorie des cordes :
La suite est ici : De l’entropie à l’hypothèse holographique
Références
[1] Michael Peskin and Daniel Schroeder, An Introduction to Quantum Field Theory (Westview Press,1995).
[2] Michael Green, John Schwarz, and Edward Witten, Superstring Theory I (Cambridge: Cambridge University Press, 1987). For a pedestrian approach : Brian Greene, The Elegant Universe : Superstrings, Hidden Dimensions and the Quest for the Ultimate Theory (Random House, (2000).
[3] Carlo Rovelli, “Loop Quantum Gravity : the first twenty five years,” Classical and Quantum Gravity, 28 (2011) :153002.
[4] Alain Connes, Noncommutative Geometry (Boston: Academic Press, 1994).
[5] Edward Witten, “Search for a realistic Kaluza-Klein theory”, Nucl. Phys. B186 (1981) : 412.
[6] Stephen P. Martin, “A Supersymmetry Primer”, arXiv :hep-ph/9709356 (1997).
[7] Barton Zwiebach, A First Course in String Theory (Cambridge University Press, 2009)
[8] Voir par exemple Philippe Brax and Carsten van de Bruck, “Cosmology and Brane Worlds: A Review,” Classical and Quantum Gravity 20, no. 9 (2003).
[9] Voir par exemple Jean-Pierre Luminet, “Interstellar Science”, Inference vol.1 Issue 2 (2014).

Toujours aussi passionnant…
Merci Jean-Pierre !
Toujours aussi passionnant…
Merci Professeur Luminet.
Bonjour, j’ai beaucoup apprécié votre article sur la théorie des cordes.
C’est effectivement une théorie tres spéculative et bien que j’y crois, je pense que la gravitation quantique a boucles, pourrait aussi etre juste.
Toutes ces théories de gravité quantique produisent des multivers hypothétiques mais j’aurais une question sur un type de multivers.
Que pensez vous du multivers d’everett, est t’il possible?
Je viens de terminer un gros article sur les différents types de multivers, y compris celui d’Everett, qui paraîtra en revue en septembre. J’en mettrai ensuite une version illustrée sur mon blog, mais pas avant cet automne. Patience donc… (et merci de me lire)
Patience dans l’azur …
Bonjour Luminet,
Franchement, je crois que l’univers préfère les équations simples. Ne trouvez-vous pas que cela est d’une complexité farfelue? Nous attendons avec impatience plutôt les vôtres!
Jamais je n’aurais pensé que les mathématiques puissent être si passionnantes/Merveilleuse idée, celle d’avoir écrit à Nina!
Bravo pour ces tours d’horizon…
Moi-même peut qualifié dans cet univers-là. J’ai entendu et vu à quoi servait l’holographie en matière d’essais non destructifs. J’ai été ravi de voir ça et les personnes qui présentaient ça avaient l’air de nous présenter comme une technique d’avenir. J’ai un neveu qui est chercheur et enseignant au CNRS en matière des Mathématiques. Il a écrit un livre sur les Mathématiques. Il s’appelle: Christophe GIRAUD.
Quelle est le nom de la revue ou sera publié votre article sur les multivers? merci
Bonjour,
Passionné depuis ma tendre enfance (j’ai 57 ans ) par le monde qui nous entoure et au fil du temps par notre univers , j’ai toujours suivi avec beaucoup d’intérêt les évolutions de la science et surtout de l’astrophysique depuis que mon papa m’a « expliqué « ce qu’était la lune quand j’avais 6 ans.
J’aurais voulu en faire mon métier , mais mes piètres notes en mathématiques m’ont contraints à d’autres activités. Pour autant, j’ai lu qq ouvrages de vulgarisation pour essayer de « comprendre » .Je me souviens notamment de celui de Hawkins « une brève histoire du temps » qu’il m’a fallu lire 3 fois pour appréhender son propos. Bref, ceci m’amène à l’une de vos brillantes conférences au collège de France sur la physique des trous noirs , et sur une de vos interview sur l’expansion de l’univers . Permettez-moi de vous poser deux questions . Je vous remercie par avance, si vous me faisiez l’honneur et le bonheur de répondre :
-Le trou noir né lors d’un effondrement gravitationnel de la matière qui se trouve donc « compacté » à l’extrême de sorte que même la lumière ne peut s’en échapper, or vous dites que certain trous noirs super massif ne sont pas forcément dense … comment cela est-ce possible , alors même que la définition du trou noir passe par la densité extrême de la matière ?
La théorie confirme une accélération de l’expansion de l’univers, or comment peut-on comprendre que l’univers soit fini et que son expansion s’accélère dans « rien » . pour que le mouvement soit possible il faut bien un espace qui permette le mouvement ? la seule façon pour moi de conceptualiser un tel phénomène, est de visualiser l’univers comme vous le décrivez ( très jolie figure géométrique )et que les objets se déplacent sur les « bords » de cette figure . imaginons que Je sois capable de lancer très fort une balle de tennis dans l’espace, elle reviendrait donc dans ma raquette avec plus de rapidité que lors de son depart ?
Humblement, et intuitivement, je penche pour la théorie selon laquelle l’univers est né de « l’explosion d’un trou noir « (notion que vous évoquez concernant la répulsivité de la matière à partir d’un certain degré de « compactage » . J’espère vivre assez longtemps pour que vous et vos confrères ayez prouvé l’existence des multiunivers, et que vous aurez enfin unifié les 2 Physiques.
Bien cordialement et avec toute mon admiration.
Patrice
Excusez la réponse tardive. La définition d’un trou noir ne passe PAS par une densité extrême, mais par la formation d’un horizon des événements (frontière du trou noir) dès qu’une certaine masse M est confinée à l’intérieur d’un certain volume critique. La formule est très simple et permet de calculer une “densité”, non pas de la matière à l’intérieur (dont on ignore le sort ultime), mais du trou noir global mesuré de l’extérieur. Et vous voyez tout de suite que les trous noirs stellaires sont en effet extrêmement denses (1 milliard de tonnes/cm3), alors que les trous noirs supermassifs ne le sont pas (0,001 g/cm3).
Par ailleurs, quand on parle d’univers fini en cosmologie, il s’agit évidemment de modèles d’espaces sans bord (comme l’hypersphère, ou bien des espaces à topologie multiconnexe). Et dans ce cas la notion d’espace extérieur dans lequel l’espace se dilaterait n’a aucun sens. l’espace, qu’il soit fini (sans bord) ou infini, se dilate en lui-même, c’est-à-dire que ses points s’écartent les uns des autres au cours du temps, c’est tout !