Archives pour l'étiquette Holographie

Astronomie, Essai, Mes publications, Sciences

L’univers holographique (5) : La quête des dualités

4 commentaires

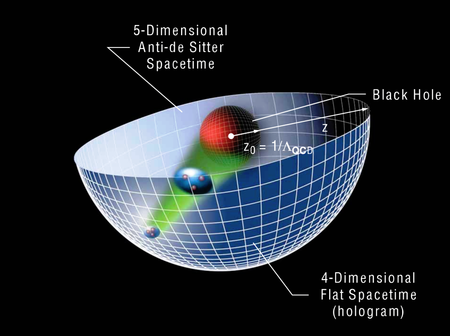
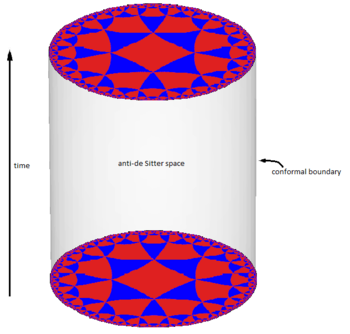
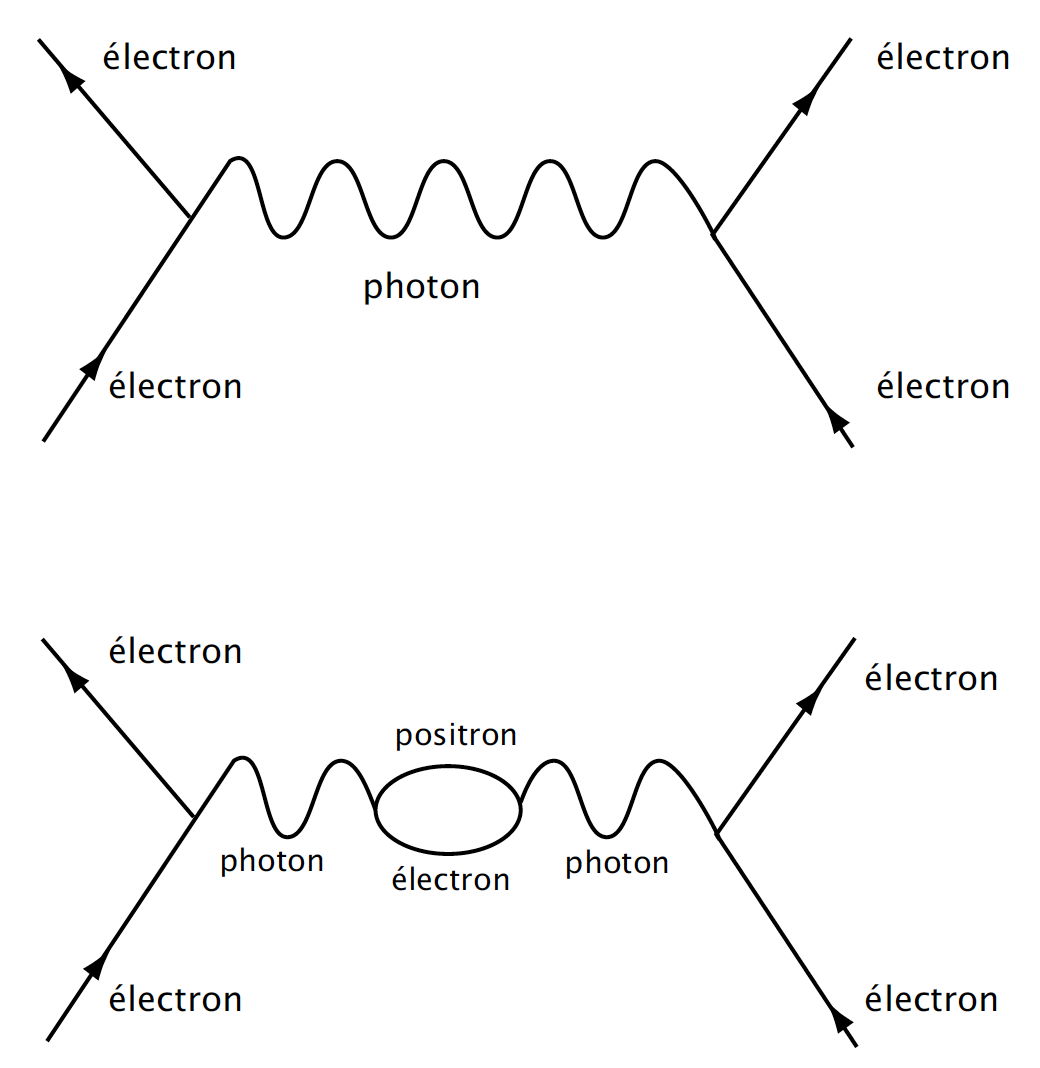
Suite du billet précédent : L’univers holographique (4) : la conjecture de Maldacena

Des centaines de chercheurs ont exploré les conséquences de la conjecture de Maldacena, avec l’espoir que la dualité jauge/gravité, sous sa forme la plus générale, puisse établir une sorte de dictionnaire pratique entre les propriétés d’un système physique en gravitation quantique, décrit par la théorie des cordes dans un espace courbe de dimensionnalité élevée (la Matrice), et un autre système physique, plus simple celui-là, décrit quantiquement par une théorie de jauge sur l’enveloppe de la Matrice – espace plat de dimensionnalité moindre. Il existe notamment une approche en théorie M,  développée en 1997 et baptisée BFSS[1], destinée à fournir une formulation numériquement calculable, qui a en outre le mérite d’établir un lien avec l’approche a priori différente de la géométrie non-commutative d’Alain Connes – pour plus de détails voir l’excellent billet de L. Sacco sur Futura Sciences.

L’avantage serait évident : certains calculs très complexes – voire impossibles – en gravité quantique pourraient être menés de façon plus simple dans le cadre de la théorie de jauge, comme on l’a vu dans le billet précédent  pour l’évaporation quantique d’un trou noir dans AdS5. Inversement, quand les champs de la théorie quantique sont fortement couplés (comme dans le plasma quark-gluon, voir ci-dessous), ceux de la théorie gravitationnelle interagissent faiblement et pourraient être plus facilement appréhendés mathématiquement. Cette dualité forte/faible permet ainsi d’explorer des aspects complexes de la physique nucléaire et de la physique de la matière condensée, en les traduisant en termes de théorie des cordes à haut degré de symétrie, plus aisément traitable.

Les possibles réalisations de la dualité jauge-gravité font aujourd’hui l’objet d’ambitieux programmes théoriques, rattachés à trois vastes domaines de la physique :

  • physique nucléaire, avec notamment l’étude du plasma quark-gluon (programme AdS/QCD)
  • physique de la matière condensée, avec l’étude des états exotiques de la matière (programme AdS/CMT)
  • relativité générale et cosmologie, avec les programmes Kerr/CFT et dS/CFT.

Développons brièvement chacun de ces programmes, en mentionnant leurs succès et leurs échecs. Continuer la lecture →

Astronomie, Mes publications, Sciences

L’univers holographique (4) : La conjecture de Maldacena

3 commentaires

Suite du billet précédent : L’univers holographique (3) : De l’entropie à l’hypothèse holographique

Juan Maldacena en 2013
Juan Maldacena en 2013

Confrontés à la difficulté d’appliquer le principe holographique à un modèle d’univers réaliste, les physiciens se sont tournés vers des modèles d’univers simplifiés, dans lesquels le principe pourrait s’appliquer. La première réalisation concrète a été l’œuvre du jeune chercheur argentin Juan Maldacena qui, en novembre 1997, publia un résultat étonnant, assorti d’une audacieuse conjecture mathématique[1].

Considérant un trou noir dans un modèle d’espace-temps à cinq dimensions macroscopiques caractérisé par une géométrie dite anti-de Sitter, il montra que les détails des phénomènes se déroulant dans cet univers, décrits par la théorie des cordes et incluant donc la gravitation, étaient entièrement codés dans le comportement de certains champs quantiques (non gravitationnels) se déroulant sur la frontière quadridimensionnelle de cet univers.

Vue d'artiste de l'équivalence
Vue d’artiste de l’hypothèse de Maldacena

L’espace-temps de de Sitter est une solution exacte des équations de la relativité générale ordinaire découverte dès 1917, vide de matière mais qui comprend une force répulsive appelée constante cosmologique, de valeur positive ; si maintenant on change le signe de la constante cosmologique, la force de répulsion devient attractive et le modèle se transforme en un espace-temps anti-de Sitter[2] . Ce dernier acquiert une géométrie spatiale hyperbolique (c’est-à-dire de courbure négative) et, bien qu’il soit infini, possède un « bord » bien défini. Pour représenter ce bord, on utilise la représentation de Poincaré du disque hyperbolique qui, à l’aide d’une transformation conforme conservant les angles mais pas les distances, ramène l’infini à distance finie. L’artiste néerlandais Mauritz Cornelius Escher a créé une célèbre série d’estampes intitulées Circle Limits dans lesquelles il utilise la représentation de Poincaré, voir par exemple [3].

Poincaré representation of the hyperbolic disc.
Représentation de Poincaré du disque  hyperbolique.

Circular Limit III, zn engraving by M.C.E. Escher, using the Poincaré representation of hyperbolic space.
Circle Limit III, une gravure de M.C.E. Escher utilisant la représentation de Poincaré de l’espace hyperbolique.
L'esapce anti-de Sitter en dimension 3 se présente comme un empilement de disques hyperboliques, chacun représentant l'état d'un univers 2D à un instant donné. L'espace-temps 3D qui en résulte resemble à un cylindre solide.
L’esapce anti-de Sitter en dimension 3 se présente comme un empilement de disques hyperboliques, chacun représentant l’état d’un univers 2D à un instant donné. L’espace-temps 3D qui en résulte resemble à un cylindre solide.

Pour l’espace-temps anti-de Sitter en dimension 5, noté AdS5, le bord est de dimension 4 et, localement autour de chaque point, ressemble à l’espace de Poincaré-Minkowski, qui est précisément le modèle d’espace-temps plat utilisé en physique non-gravitationnelle. Cela signifie qu’un trou noir dans l’espace-temps anti-de Sitter 5D est strictement équivalent à un champ de particules et de rayonnement existant dans l’espace-temps plat 4D de la frontière. Or, cette dernière description fait appel à des théories de champs quantiques bien connues et maîtrisées, analogues aux champs de Yang-Mills utilisés par exemple en chromodynamique quantique (qui est la théorie de l’interaction forte). Notons cependant qu’aux cinq dimensions spatiales de l’espace-temps anti-de Sitter il faut rajouter cinq dimensions spatiales compactifiées en forme de sphère S5, afin de traiter le problème dans le cadre de la théorie des cordes standard à dix dimensions.

Continuer la lecture →

Actualités, Mes publications, Sciences

L’univers holographique (2) : La gravité quantique façon théorie des cordes

10 commentaires

Suite du billet précédent L’univers holographique (1) : le paradoxe de l’information

Le paradoxe de l’information lié aux trous noirs reflète notre incapacité actuelle à élaborer une théorie cohérente de la gravité quantique. L’approximation semi-classique de Hawking cesse d’être valide quand le trou noir devient suffisamment petit pour que le rayon de courbure à l’horizon des événements atteigne la longueur de Planck, 10-33 cm, autrement dit lorsque non seulement la matière et l’énergie, mais aussi le champ gravitationnel doivent être quantifiés. La description finale de l’évaporation et la restitution partielle ou complète de l’information exigent donc un traitement complet en gravité quantique, branche fondamentale de la physique qui cherche à décrire la gravitation en utilisant les principes de la mécanique quantique.

Richard Feynman (1918-1988), prix Nobel de physique 1965, auteur des diagrammes du même nom.
Richard Feynman (1918-1988), prix Nobel de physique 1965, auteur des diagrammes du même nom.

L’application de la mécanique quantique aux objets physiques tels que le champ électromagnétique, qui s’étendent dans l’espace et le temps, a connu un succès éclatant avec la théorie quantique des champs[1]. Celle-ci forme la base de la compréhension du modèle standard de la physique des particules élémentaires, rendant compte des interactions électromagnétiques, nucléaire forte et nucléaire faible. Elle permet de calculer les probabilités d’événements en utilisant les techniques de la théorie des perturbations. Les diagrammes de Feynman décrivent les chemins de particules ponctuelles et leurs interactions. Chaque diagramme représente une contribution à un processus d’interaction. Pour leurs calculs, les physiciens additionnent en premier lieu les contributions les plus fortes, puis les plus petites, et ainsi de suite, jusqu’à atteindre la précision désirée.

Diagramme de Feynman. Lorsque deux particules (ici deux électrons venant du bas) interagissent, elles peuvent le faire « simplement », en échangeant un seul photon (schéma du haut). Mais ce photon peut lui-même se matérialiser puis de dématérialiser en chemin. Sur le schéma du bas, par exemple, il crée une paire électron-positron qui recrée ensuite le photon. Si l’on tient compte de cette aventure, la description de l’interaction des deux électrons de départ n’est plus la même. Cela n’est en fait que la « première correction ». En effet, il peut arriver au photon des histoires beaucoup plus compliquées qui représentent des corrections d’ordre 2,3,4… La physique quantique exige de tenir compte de l’infinité de ces corrections pour le moindre calcul. Cette difficulté considérable a conduit à incorporer à la physique quantique l’idée de renormalisation.
Diagramme de Feynman. Lorsque deux particules (ici deux électrons venant du bas) interagissent, elles peuvent le faire « simplement », en échangeant un seul photon (schéma du haut). Mais ce photon peut lui-même se matérialiser puis de dématérialiser en chemin. Sur le schéma du bas, par exemple, il crée une paire électron-positron qui recrée ensuite le photon. Si l’on tient compte de cette aventure, la description de l’interaction des deux électrons de départ n’est plus la même. Cela n’est en fait que la « première correction ». En effet, il peut arriver au photon des histoires beaucoup plus compliquées qui représentent des corrections d’ordre 2,3,4… La physique quantique exige de tenir compte de l’infinité de ces corrections pour le moindre calcul. Cette difficulté considérable a conduit à incorporer à la physique quantique l’idée de renormalisation.

 

Mais ce procédé ne marche que si les contributions deviennent réellement négligeables à mesure qu’un plus grand nombre d’interactions est pris en compte. Lorsqu’il en va ainsi, la théorie est dite “faiblement couplée” et les calculs convergent vers des valeurs physiques finies. S’il en va différemment, la théorie est dite “fortement couplée” et les méthodes standard de la physique des particules échouent. C’est notamment ce qui arrive avec le graviton, supposé être la particule médiatrice du champ gravitationnel. Le graviton, créant de la masse-énergie, interagit avec lui-même, ce qui crée de nouveaux gravitons, qui à leur tour interagissent, et ainsi de suite, jusqu’à la divergence. L’échec de la technique des perturbations pour quantifier la gravité a donc conduit les physiciens à explorer d’autres voies. Continuer la lecture →

Actualités, Mes publications, Sciences

L’univers holographique (1) : le paradoxe de l’information

19 commentaires

Ce billet est le premier d’une série de 6 reprenant un article initialement publié en anglais dans la revue Inference : The International Review of Science, auquel j’ai rajouté des illustrations à caractère pédagogique.

Introduction

Lors d’un exposé donné le 25 août 2015 au KTH Royal Institute of Technology à Stockholm qui a fait l’objet d’un grand tapage médiatique, Stephen Hawking a annoncé avoir résolu un problème de la physique appelé paradoxe de l’information [1]. Ce dernier illustre un conflit potentiel entre la mécanique quantique et les modèles de trou noir décrits par la relativité générale ; à ce titre, il joue un rôle central en physique fondamentale et divise la communauté des théoriciens depuis quatre décennies. Selon Hawking, toute l’information sur la matière et l’énergie contenue dans le volume 3D du trou noir résiderait en réalité sur sa surface 2D, l’horizon des événements, codée sous forme d’hologramme.

hologram1
Un hologramme est une photographie d’un type particulier qui engendre une image tridimensionnelle quand on l’éclaire de façon appropriée ; toute l’information décrivant une scène en trois dimensions est encodée dans le motif de zones claires et sombres inscrit sur un film à deux dimensions.

Cette information pourrait ensuite être entièrement récupérée (bien que sous forme chaotique) grâce au rayonnement libéré lors de son évaporation quantique – un processus initialement prédit par le même Hawking quarante ans auparavant.

L’idée n’est pas nouvelle : elle fait appel à un modèle d’univers holographique précédemment étudié par des centaines de physiciens, et objet d’un tel engouement qu’il a conduit certains d’entre eux à imaginer des scénarios parfaitement surréalistes. Par exemple, S. Mathur a proposé qu’au lieu d’être détruit par des forces de marée gravitationnelles ou par un pare-feu quantique, un astronaute tombant dans un trou noir serait simplement converti en hologramme, sans se rendre compte de rien [2].

A l’annonce de Hawking la communauté scientifique a donc dans son ensemble réagi avec beaucoup de prudence et de scepticisme, pour ne pas dire d’embarras devant l’annonce prématurée d’une idée non élaborée sur le plan technique : comment l’information s’inscrit-elle dans l’horizon des événements, comment est-elle restituée au monde extérieur, aucun détail n’a encore été donné.[3]

Pour y voir plus clair, un retour en arrière sur la thermodynamique des trous noirs s’impose.

Thermodynamique des trous noirs et paradoxe de l’information

Au cours des années 1970 – âge d’or de la théorie des trous noirs en relativité générale classique -, il a été démontré d’une part que l’état final d’un trou noir à l’équilibre ne dépendait que de trois paramètres : sa masse M, son moment angulaire J et sa charge électrique Q, ce qui paradoxalement faisait de lui l’objet le plus simple de toute la physique ; d’autre part, que la dynamique des trous noirs en interaction se résumait en quatre lois présentant une analogie extrêmement frappante avec celles de la thermodynamique usuelle[4]. En particulier, la seconde loi stipule que l’aire d’un trou noir ne peut jamais décroître au cours du temps. Ce résultat fondamental suggère une connexion étroite entre l’aire d’un trou noir et l’entropie d’un système thermodynamique. Continuer la lecture →