Pour monter sur un sommet à 3712 mètres d’altitude, comme la Grande Ruine dans le massif de Ecrins (image mise en avant @Hervé Lehning), en partant d’un refuge situé à 3169 mètres d’altitude (le refuge Adèle Planchard), il est nécessaire de passer par toutes les altitudes intermédiaires.

Le Théorème des Valeurs Intermédiaires (ou TVI)
Ce résultat de bon sens correspond à un théorème de mathématiques concernant les fonctions continues sur un intervalle réel à valeurs réelles. La plupart des fonctions qu’on rencontre en mathématiques sont continues sauf, éventuellement, en quelques points exceptionnels, appelés pour cela points de discontinuité. Physiquement, dans la pratique, ces points correspondent souvent à des sauts.
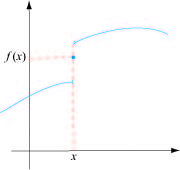
Le théorème des valeurs intermédiaires peut s’illustrer ainsi :
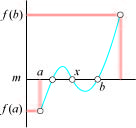
Utilité
L’utilité pratique essentielle de ce théorème est de montrer l’existence de racines d’équations : si une fonction continue change de signe entre deux points a et b, elle s’annule entre ces deux points.
On en déduit, par exemple, qu’une fonction continue sur un segment [a, b] à valeurs dans lui-même admet au moins un point fixe, c’est-à-dire un point x tel que f (x) = x. Pour le démontrer, il suffit de remarquer que la fonction g définie par g (x) = f (x) – x change de signe entre a et b.
