Penchons-nous sur la forme des tipis des indiens d’Amérique. Il s’agit d’un cône dont la hauteur vaut environ 75 % du diamètre de la base. Des calculs montrent que cette forme minimise la toile à utiliser pour un volume donné, comme les abeilles économisent la cire pour créer leurs alvéoles. Est-ce un hasard ? Difficile de répondre à la question car d’autres paramètres comme la solidité de l’ensemble entrent en jeu. Peu importe, ces problèmes d’optimisation se retrouvent souvent dans la nature comme dans la vie pratique.
Analyse mathématique
Analysons celui-ci mathématiquement. Un tipi est une tente conique caractérisée par le rayon de sa base, R, et par sa hauteur, que nous notons proportionnellement à R, k R, car le problème tient essentiellement à ce rapport k. La capacité du tipi est égale à son volume et la surface de toile, à son aire latérale.
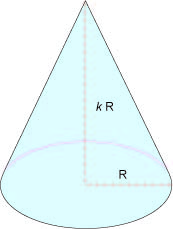
Le volume est égal à Pi / 3 multiplié par le carré du rayon R et par la hauteur k R. Imposer un volume de 10 mètres cube (par exemple) lie le rapport k au rayon R. L’aire latérale dépend alors uniquement de ce rapport. Cette dépendance se traduit par une courbe en forme de J à l’envers. Nous y constatons un minimum de l’aire pour une valeur de k de l’ordre de 1,4, autrement dit pour une hauteur 40 % supérieure au rayon de la base. De façon plus précise, le calcul différentiel montre que ce minimum est atteint pour k égal à la racine carrée de 2, ce qui fait 1,414 à 0,001 près.
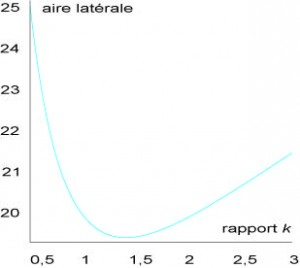
À volume égal, l’aire latérale du tipi est donc minimale pour un rapport proche de 1,4. La courbe montre de plus que la variation de l’aire latérale est faible autour de ce rapport, ce qui explique que, dans la pratique, il oscille autour de 1,4.
