Dans Les Eléments, Euclide pose plusieurs axiomes et définitions de la géométrie plane puis démontre un certain nombre de théorèmes. Entre les deux, il postule que, par un point donné, il passe une et une seule parallèle à une droite donnée. En apparence, il s’agit d’un théorème sans preuve. Des générations de mathématiciens ont essayé de le démontrer sans jamais y arriver. Avant d’analyser la question, il est nécessaire de revenir sur les axiomes d’Euclide.

Les axiomes d’Euclide

Il serait fastidieux de passer en revue les axiomes et les définitions de la géométrie plane d’Euclide. Pour en comprendre l’origine, il suffit de revenir au mythe de la caverne, une allégorie où Platon estime que le monde réel est rempli d’objets dont les modèles sont ailleurs, dans le monde des idées. De la même façon, les points, droites et angles d’Euclide sont les idées des points, droites et angles réels tels qu’un maçon les utilise. Qu’est-ce qu’une droite ? Pour le comprendre, faites comme le maçon. Prenez une corde et deux piquets. Plantez les deux piquets et tendez la corde. Vous réalisez ainsi le plus court chemin entre eux.

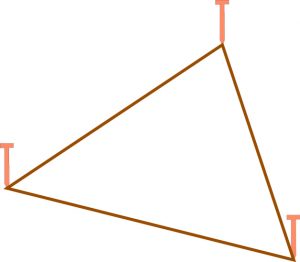
Avec la même méthode et trois piquets, vous fabriquez un triangle donc trois angles.

Une preuve sous condition

Une petite figure suffit pour démontrer ce résultat. Pour la tracer, en plus de notre corde et de nos piquets, munissons-nous d’un rapporteur capable de reporter un angle donné le long d’une droite, en un point.

Considérez un triangle ABC, prolongez le côté AB en BE et du point B, en utilisant le rapporteur, portez la droite BD de sorte que l’angle CBD soit égal à l’angle ACB (en rouge tous les deux). De même, portez la droite BD’ de façon que l’angle EBD’ soit égal à l’angle BAC (en bleu).

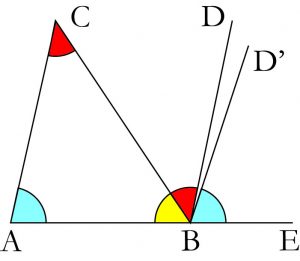
Les droites BD et BD’ sont parallèles à la droite AC (les angles rouges et jaunes sont alternes internes). Elles sont donc identiques puisque, d’un point, on ne peut tracer qu’une parallèle à une droite donnée. Les trois angles du triangle ABC se reportent ainsi en B pour former un angle plat, c’est-à-dire 180°. Nous avons ainsi démontré que la somme des angles d’un triangle est égale à 180° … si le postulat d’Euclide est vrai.

L’idée qui dépostule

Quand on dessine la figure précédente sur une feuille de papier, les droites BD et BD’ sont confondues. Coupons le papier le long de la demi-droite BD et déplaçons BD’ sur BD, la feuille se courbe. Elle devient comme un sommet de montagne et la somme des angles du triangle, supérieure à 180°. Au contraire, en écartant BD’ de BD, la feuille se courbe dans l’autre sens. Elle devient comme un col de montagne et la somme des angles du triangle, inférieure à 180°.

Triangle sur la sphère

Pour développer cette idée, reprenons les axiomes d’Euclide sans le postulat en nous plaçant avec nos piquets, notre corde, notre rapporteur et nos définitions sur une sphère. Le plus court chemin entre deux points est obtenu en suivant l’arc de grand cercle entre eux.

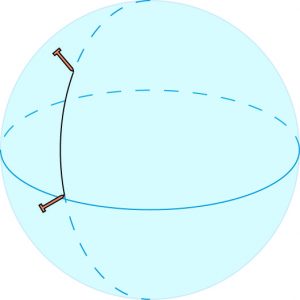
Sur une sphère, deux grands cercles se coupent toujours. Autrement dit, deux droites ne sont jamais parallèles ! Le postulat d’Euclide y est faux et notre démonstration lumineuse aussi. Dans ce cas, les deux droites BD et BD’ ne se recoupent pas, l’angle DBD’ n’est pas nul. La somme des angles du triangle est donc supérieure à 180°. Pour vous en convaincre davantage, prenez un globe terrestre miniature, deux points sur l’équateur et dessinez le triangle formé avec l’un des pôles. La somme de ses angles est égale à 180° plus l’angle au pôle, elle est donc strictement supérieure à 180°.

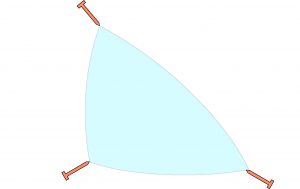
Triangle sur une selle de cheval

Si nous nous plaçons sur une surface différente comme un col de montagne ou une selle de cheval, la somme des angles d’un triangle devient inférieure à 180°. Sur la figure de notre démonstration, les droites BD et BD’ se couvrent.

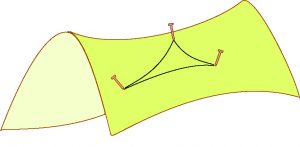
Les surfaces comme les plans, les cylindres ou les cônes où la somme des angles d’un triangle est égale à 180° sont dites de courbure nulle, celles comme la sphère ou les ellipsoïdes où la somme des angles est supérieure à 180°, de courbure positive et celles comme la selle de cheval où la somme des angles est inférieure à 180°, de courbure négative. Ces surfaces ne sont pas des plans euclidiens.

Aire d’un cercle

De même, grâce à un piquet et une corde, sur toute surface, nous pouvons tracer un cercle de rayon R. Si la courbure de la surface est nulle, son aire est égale à p R². Si elle positive, elle est inférieure, sinon elle est supérieure.

Courbure d’un espace

Notre vision en trois dimensions nous permet d’admettre facilement ces résultats. Imaginons des êtres plats « collés » sur une surface de dimension deux pour lesquels, elle serait l’univers entier. Incapable d’en sortir, il ne verrait pas sa courbure. Il pourrait cependant tracer un triangle, mesurer ses angles et déterminer ainsi si son univers a une courbure positive, négative ou nulle.

De même, un extraterrestre vivant et voyant dans un monde en dimension quatre pourrait « voir » la courbure de notre univers. Nous y sommes trop englués pour cela. Le même phénomène existe pourtant et nous pouvons le tester : il suffit de mesurer le volume d’une sphère ou la somme des angles d’un triangle. Jusqu’à présent, les mesures effectuées font penser que notre univers est de courbure quasiment nulle.