En 1973, Berkeley, l’université américaine, fut poursuivie pour discrimination envers les filles. L’affaire semblait claire. Parmi les candidates, seule 35 % étaient retenues alors que 44 % des candidatures masculines l’étaient. L’étude a été précisée sur les six départements les plus importants, que nous notons ici de A à F.
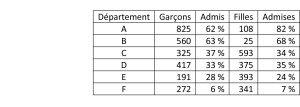
Ce tableau ne montre aucune discrimination envers les femmes. Au contraire, le taux d’admission des filles dans le principal département (A) est nettement supérieur à celui des garçons. L’explication vient quand on regarde le nombre de candidatures dans ces départements. Les femmes semblent avoir tendance à postuler en masse à des départements très sélectifs. Dans ceux-ci, leur taux d’admission est à peine plus faible que celui des hommes. Dans les autres, elles sont plus largement sélectionnées que les hommes. Quand on fait la moyenne globale, ce sont les départements sélectifs qui ont plus de poids, puisqu’elles y postulent en masse. Ce paradoxe a été étudié par Edward Simpson (né en 1922). On le retrouve dans de nombreux cas.


