Vous lisez dans la presse que la Française moyenne mesure 1 mètre 63. Si vous rencontrez une Française, quelle est la probabilité qu’elle ait cette taille ?
Moyenne et répartition
En l’absence d’informations supplémentaires, impossible de répondre à cette question. Pour cela, il faut connaître la répartition de la taille des Françaises. De plus, la question est mal formulée : la Française moyenne est un mythe … il est préférable de parler de la taille moyenne des Françaises. En fait, elles se répartissent en 25 % de petites (1 mètre 54 en moyenne), 50 % de moyennes (1 mètre 63 en moyenne) et 25 % de grandes (1 mètre 72 en moyenne). La répartition exacte suit une courbe en forme de cloche comme c’est le cas généralement quand on étudie une population homogène sous un certain critère.
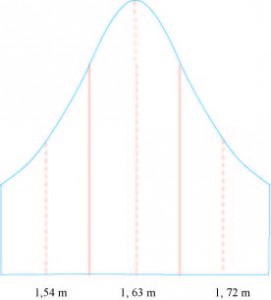
Cette courbe ne suffit pas non plus pour répondre à la question, même si elle donne l’idée que la probabilité qu’une femme donnée mesure 1 mètre 63 se situe entre 10 et 20 %. Les données statistiques sont donc à analyser avec prudence.


