Sans doute pour éviter les nombres négatifs, Daniel Gabriel Fahrenheit (1686 – 1736) fixa l’origine des températures (0° Fahrenheit) à la plus basse qu’il ait observée. C’était durant l’hiver 1709 dans la ville de Dantzig, où il habitait. Pour 100° Fahrenheit, il choisit la température corporelle d’un cheval sain ! Dans son système, l’eau gèle à 32° et elle bout à 212° environ.

L’absolu du zéro
Ces choix étranges de Fahrenheit s’expliquent par la réticence de l’époque devant les nombres négatifs. On préférait d’ailleurs parler de quantités plutôt que de nombres. Il s’agissait d’artifices de calcul pour résoudre des équations, dont on écartait ensuite les solutions négatives. Tout en étant une origine, zéro véhicule une idée d’absolu, en dessous duquel on ne peut aller, comme on le voit chez Blaise Pascal (1623 – 1662) qui, dans ses Pensées, écrit cette phrase surprenante :
Trop de vérité nous étonne ; j’en sais qui ne peuvent comprendre que, qui de zéro ôte 4, reste zéro.
Cette idée a perduré jusqu’au XIXe siècle, Lazare Carnot (1753 – 1823) écrivait encore :
Pour obtenir réellement une quantité négative isolée, il faudrait retrancher une quantité effective de zéro, ôter quelque chose de rien : opération impossible. Comment donc concevoir une quantité négative isolée ?
La solution de Cauchy
La question semble cependant résolue avec Augustin Louis Cauchy (1789 – 1857) qui, dans son Cours d’analyse de l’Ecole royale polytechnique définit les nombres relatifs comme une partie numérique précédée d’un signe + ou – :
Le signe + ou – placé devant un nombre en modifiera la signification, à-peu-près comme un adjectif modifie celle du substantif.
Conversion entre degrés Celsius et degrés Fahrenheit
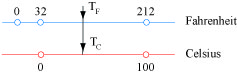
Les variations étant linéaires dans les deux cas, la relation est affine, c’est-à-dire de la forme : TF = a TC + b. Les deux coïncidences donnent les relations : b = 32 et 100 a + b = 212 d’où : a = 1,8 et b = 32. Nous en déduisons la formule : TF = 1,8 TC + 32. Ainsi la température de 37° Celsius donne : 1,8 x 37 + 32 = 98,6° Fahrenheit.
