Le jeu de la vie, inventé en 1970 par John Conway, n’est pas vraiment un jeu. Ce terme est cependant moins rébarbatif que celui d’automate cellulaire, qui est pourtant plus exact. Il trouve ses origines dans des travaux conduits par John von Neumann dans les années 1940. Nous garderons la métaphore du jeu pour en parler, même si certains trouveront le terme mal adapté quand il s’agit de maladies potentiellement mortelles. L’essentiel est d’aider la compréhension. Voyons quelles en sont les règles.

Les règles du jeu de la vie

Pour jouer, prenez un damier et des pions. Les cases sont considérées comme des cellules ; elles peuvent être mortes ou vivantes. On utilise les pions pour matérialiser les cellules vivantes. Au début du jeu, on place des pions sur n’importe quelle case. On joue ensuite par étapes selon les règles suivantes :

— une cellule morte entourée de trois cellules vivantes ressuscite, sinon elle reste morte ;

— une cellule vivante reste en vie si elle a deux ou trois voisines vivantes, sinon elle meurt.

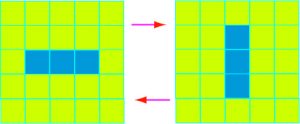
Bien que l’évolution du jeu soit complètement déterminée par la disposition initiale des cellules, on n’en assiste pas moins à quelques situations qui peuvent paraître surprenantes. Ainsi, en alignant tout simplement trois cellules vivantes les unes à côté des autres, on obtient une situation où les trois cellules se reproduisent, alignées horizontalement puis verticalement et ainsi de suite.

Le jeu des épidémies

 

Ce jeu est loin d’être un simple amusement : il s’agit d’un exemple de ce que l’on nomme « automate cellulaire », particulièrement utile pour modéliser les processus d’expansion des épidémies comme des épizooties. En préalable à ce type d’application, il est nécessaire d’étendre le damier à l’infini. Au départ, toutes les cellules sont saines. On place une cellule infectée puis on « joue » avec la règle probabiliste suivante :

— les cellules voisines de la cellule infectée sont infectées au coup suivant avec la probabilité p ;

— la cellule meurt ou est immunisée le coup suivant.

La question qui intéresse autant les épidémiologistes que le grand public est donc : « Pour quelles valeurs de p, la maladie se propage-t-elle au monde entier ? »

Un modèle probabiliste

Le modèle est ici « probabiliste », et donc on ne peut prédire à l’avance ce qui va se produire dans un cas particulier. Pour avoir une idée rapide de l’évolution moyenne du système, le mieux est de procéder à une simulation. Pour cela, on « joue » selon les règles énoncées ci-dessus en utilisant un générateur de nombres pseudo-aléatoires et on comptabilise le nombre de cellules infectées. En jouant cent fois de suite et en faisant la moyenne des résultats, on obtient une mesure de l’expansion moyenne de l’épidémie.

Taux critique

En dessous d’un certain taux de contamination p, l’épidémie ne s’étend pas. En revanche, au dessus de ce taux, elle envahit le monde entier. Dans le cadre de notre modèle simplifié, le taux critique se situe entre 30 % et 40 %. Une maladie ne devient épidémique que si ce taux est dépassé. Comment ce modèle peut-il être adapté pour bien modéliser différents types d’épidémies ou d’épizooties ? Tout d’abord, on peut modifier le voisinage de chaque cellule, composé ici de huit cellules — les spécialistes parlent de voisinage de Moore, du nom d’Edward Moore, l’un des fondateurs de la théorie des automates. On utilise souvent un voisinage plus simple, dit de von Neumann, constitué des quatre cellules partageant un côté avec la cellule considérée. Avec ce nouveau modèle, le taux critique pour lequel une maladie devient épidémique se situe aux alentours de 60 %. On peut également améliorer le modèle en tenant compte du temps pendant lequel une cellule infectée est contagieuse puis du taux de mortalité et d’immunité ainsi que du temps d’immunité. On arrive ainsi à retrouver la façon dont se sont propagées des épidémies comme la peste dans l’Europe médiévale. Une première vague a tué le tiers de la population en se propageant à partir d’un épicentre situé dans un port, suivie de plusieurs répliques plus faibles, toutes partant du même point. Ces répliques correspondent à la fin de certaines immunités.

La confrontation avec les données épidémiologiques a permis de montrer que ce type de modèles a une certaine pertinence pour toutes les maladies qui se propagent par contact direct : grippe, tuberculose, coronavirus ou même sida. En revanche, il ne fonctionne plus lorsque la maladie se propage via un agent infectieux, comme dans le cas du paludisme ou du chikungunya.

Géométrie des contagions

Comment considérer maintenant la notion de « cellule voisine » dès que l’on évoque les réseaux de transports aériens, maritimes ou terrestres ? Dans le cas d’une épidémie de grippe humaine, l’aéroport de Paris est voisin de celui de Hong-Kong. Dans le cas d’une épizootie de grippe aviaire, deux élevages fréquentant le même marché aux bestiaux sont voisins. On doit de plus tenir compte des migrations naturelles des oiseaux sauvages. Dans tous ces cas, on retrouve la notion de réseaux.

En modifiant le modèle du jeu, on peut passer du cas où chaque cellule représente un individu à celui où elle représente un domaine où les individus sont en relation constante : un élevage de volaille dans le cas de la grippe aviaire, une ville dans le cas de la tuberculose, du sida ou de la grippe humaine. Ces domaines sont reliés entre eux pour former un réseau. Dans chaque cellule, la modélisation suit une autre logique, celle du modèle « SIR » dû à William Kermack et Anderson Mac Kendrick en 1927 (voir l’article correspondant sur ce blog). Ce modèle compartimente la population en trois classes : S, la classe des individus susceptibles d’attraper la maladie, I, celle de ceux qui en sont infectés (et contagieuses) et R, ceux qui en sont guéris (et immunisés) ou décédés.

Seuil de propagation

On considère l’évolution de ces trois classes dans le temps en fonction de deux taux mesurables expérimentalement. Le premier (a) est le taux de contagion de la maladie pour un infecté, c’est-à-dire la probabilité pour qu’un individu susceptible attrape la maladie après contact avec un individu infecté. Le second taux (b) mesure le passage de l’état I à l’état R.

Après un laps de temps t, on compte a I S t infectés supplémentaires et R augmente de b I t. La variation du nombre d’infectés est donc égale à a S – b multiplié par I t. La condition pour que la maladie se propage (et donc donne lieu à une épidémie) est que le nombre de malades infectés augmente, c’est-à-dire que : a S – b > 0. Le quotient b / a a donc valeur de seuil. Si le nombre de sujets susceptibles est strictement inférieur à ce seuil, la maladie ne s’étend pas. Sinon, elle donne lieu à une épidémie (ou à une épizootie).

D’une façon qui peut paraître paradoxale, l’apparition d’une épidémie ne dépend donc pas du nombre de personnes infectées mais du nombre de personnes susceptibles d’attraper la maladie ! Cette remarque justifie à elle seule les politiques de vaccination, même avec un vaccin peu efficace.