L’Antiquité grecque s’est passionnée du problème d’Apollonius (trois siècles avant notre ère) sans doute sans y voir la moindre application. Songez ! Étant donné trois cercles du plan, il s’agit de trouver les cercles qui leur sont tangents. Il fallut attendre François Viète (1540 – 1603) pour qu’il trouve une solution complète. Au maximum, huit cercles sont solutions.
Repérage acoustique de l’artillerie
Une idée pour repérer les pièces d’artillerie est d’utiliser le son produit lors de la mise à feu. Les instruments essentiels pour ces repérages sont des microphones, dispositifs inventés à la fin du XIXe siècle. S’ils sont adaptés aux basses fréquences et ignorent les autres, les sons de l’artillerie lourde sont distingués des autres bruits du champ de bataille. Il faut en utiliser au moins trois, reliés à un appareil d’enregistrement effectuant un tracé sur un même rouleau enregistreur afin de comparer les instants de réception du son.
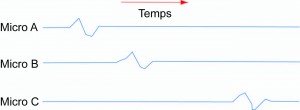
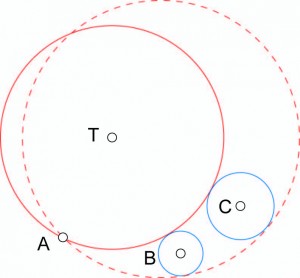
Dans le cas de l’enregistrement ci-dessus, l’onde sonore venant du canon ennemi (en T) se déplace selon un cercle de centre T. Elle atteint d’abord le point A où est placé le premier microphone puis le point B où est placé le second après un temps t mesurable sur l’enregistrement et enfin le point C après un temps t’ (toujours après le point A). En tenant compte de la vitesse du son, la distance de T à A est égale à un nombre R, qu’il s’agit de déterminer, celle de T à B à R + r où r correspond à la distance parcourue par le son pendant le temps t et enfin la distance de T à C égale à R + r’ où r’ correspond à la distance parcourue par le son pendant le temps t’.
Si T est connu, le cercle de centre T et de rayon R passe par A et est tangent au cercle de centre B et de rayon r ainsi qu’au cercle de centre de centre C et de rayon r’, ce qui se résume en une figure bien connue des mathématiciens de l’époque, au problème d’Apollonius, l’un des cercles étant de rayon nul :
Résolution du problème
De nos jours, ce problème est résolu par la géométrie analytique et un logiciel détermine directement les coordonnées de la position de la batterie ennemie (système de localisation de l’artillerie par acoustique, SL2A). Ce système peut être couplé de nos jour avec un radar de contrebatterie (RCB), qui a cependant le défaut d’être lui-même repérable puisqu’un radar émet des ondes, contrairement au système acoustique.

On peut également réduire ce problème à une question d’intersection de deux hyperboles mais, au temps de la Grande Guerre, le calcul se faisait graphiquement sur une carte avec un jeu de disques de divers rayons par tâtonnement sachant que la portée maximale des canons était connue.
La méthode a amélioré le repérage des batteries ennemies mais elle n’est pas toujours précise car la vitesse du son dépend de facteurs météorologiques comme la température et la vitesse du vent. De plus, l’artillerie était souvent utilisée en grand nombre simultanément ce qui rendait délicat le repérage individuel de chaque batterie.
Laissons la conclusion sur l’importance de ces recherches à Paul Painlevé, mathématicien et ministre de la guerre en 1917, dans une allocution après la victoire : les mathématiques les plus abstraites ou les plus subtiles ont participé à la solution des problèmes de repérage et au calcul des tables de tir toutes nouvelles qui ont accru de 25 pour 100 l’efficacité de l’artillerie.
