Le problème de Napoléon que nous voulons évoquer ici n’est pas d’ordre militaire ou climatique, comme celui qui lui fit oublier qu’il pouvait faire froid en Russie en hiver. Non, il est d’ordre mathématique, de géométrie très classique.
L’énoncé du problème
Le voici : un cercle étant donné (sans son centre), il s’agit de le trouver en utilisant seulement un compas (donc sans la fameuse règle des constructions usuelles). Pour ceux qui s’intéressent à cette question d’un autre temps, le petit dessin qui suit montre comment s’y prendre.
Ce dessin résume la construction du centre du cercle : on choisit A sur le cercle puis on construit les points B, C, … jusqu’à G qui est le centre cherché.
Un intérêt marqué pour les sciences
L’intérêt que portait Bonaparte aux sciences ne se limitait pas à ce problème dont on ne sait si la solution ci-dessus est de lui ou non. Sous son règne, les sciences étaient à l’honneur et les scientifiques aussi. Ainsi, le grand mathématicien Joseph Fourier fut aussi préfet de l’Isère. A ce titre, on lui doit la route de Grenoble à Briançon passant pas le col du Lautaret. L’appétit de Napoléon pour les sciences ne prit pas fin avec son règne puisqu’il emporta une vraie bibliothèque scientifique dans l’île de Sainte Hélène, dont le cours de mathématiques de Sylvestre-François Lacroix, qu’il annota de sa main.
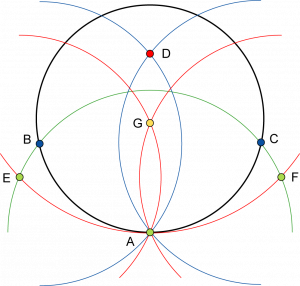
La voûte semble être née plate. Pour permettre une ouverture dans un mur, traditionnellement, on posait au-dessus une pierre assez longue en guise de linteau, comme dans le cas de cette porte dans les ruines de Délos en Grèce.
Une porte à Délos.
S’ils ne disposaient pas de pierres assez longues, dès l’Antiquité, les architectes ont trouvé un moyen d’y pallier en utilisant plusieurs pierres plus petites disposées de façon à ce que le poids de l’ensemble bloque le linteau. La pierre centrale, en coin dans le dispositif, est appelée la clef de voute. Il est probable que cette méthode ait été trouvée par essais et erreurs même si elle s’explique très bien par la pesanteur, en calculant le bilan des forces exercées, ce que les ingénieurs savaient faire à l’époque d’Archimède (IIIe siècle avant notre ère). Il est important que les appuis sur les côtés soient suffisamment lourds pour ne pas être déplacés par la poussée latérale exercée par le linteau.
Linteau de porte avec clef de voûte (au centre).
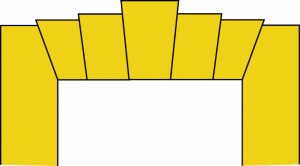
Pour des ouvertures plus importantes, les architectes ajoutaient simplement des colonnes ou des caryatides, qui sont des colonnes sculptées en forme de femmes (la variante masculine se nommant Atlante), ce qui donne des édifices comme l’Érechthéion sur l’Acropole d’Athènes. Ces colonnes étaient alors surmontées de linteaux comme une porte.
Colonnes et caryatides de l’Érechthéion sur l’Acropole d’Athènes.
La même idée fonctionne avec des voûtes en arc de cercle comme en construisaient les Romains, mais qu’on trouve déjà chez les Égyptiens et les Grecs, même si c’est dans des constructions utilitaires comme des entrepôts ou des canalisations. Ici encore, le poids de la voûte s’exerce sur les piliers latéraux dont la masse assure la stabilité de l’ensemble.
Voûte avec clef maintenant l’ensemble.
Ces voûtes peuvent être prolongées pour former le plafond d’une salle, elles servent aussi à construire des ponts comme les deux ponts d’Albi, le vieux datant de 1040 et le neuf de 1867.
Le pont vieux d’Albi (en premier plan) a des arches ogivales, le pont neuf (en second plan) a des arches en plein cintre.
Les dômes
Mis à part les toits plats ou en pentes et les voûtes, les Grecs eurent l’idée de toits hémisphériques, autrement dit de dômes. Le principe de la stabilité de ces structures repose sur des murs solides, calculés pour soutenir le dôme, comme pour les voûtes. Les dômes de l’Antiquité comme celui de Sainte Sophie à Constantinople (aujourd’hui Istanbul) ont des assises massives, qui permettent la stabilité du tout même si le dôme de Sainte Sophie s’écroula en 1346, suite à un séisme survenu deux ans plus tôt.
Dôme posé sur un tambour octogonal, de la cathédrale Santa Maria del Fiore à Florence, vu de son campanile.
La cathédrale Santa Maria del Fiore de Florence posa un problème plus épineux. En 1418, la cathédrale était achevée mis à part un trou béant de 45 mètres de diamètre au-dessus d’un tambour octogonal de 53 mètres de haut. D’après les plans de l’architecte initial, décédé depuis longtemps, un dôme devait reposer sur ce tambour. L’ennui est que personne ne savait ni comment le faire tenir sur une structure aussi légère, ni comment le construire sans échafaudage en bois, comme on le faisait à l’époque mais impossible ici du fait de la trop grande portée. La question fut mise au concours et Filippo Brunelleschi (1377 – 1446) le remporta avec une double structure légère, une à l’extérieur, l’autre à l’intérieur. Finalement, le tout fut monté progressivement par anneaux horizontaux et sans échafaudage, un peu comme on le fait dans certains pays d’Afrique pour des cases en forme d’ogive. Ce type de construction semble venir de l’antique Nubie, car on en trouve en haute Égypte.
Construction d’une case obus sans échafaudage (architecture Mousgoum).
John Horton Conway, né le 26 décembre 1937 et mort lors de la pandémie de Coronavirus le 11 avril 2020, est l’un des mathématiciens les plus originaux du XX° siècle. Il est particulièrement connu pour sa création du jeu de la vie, qui est déjà l’objet d’un article de ce blog.
Un cercle dans un triangle
En pleine époque des maths modernes, le malicieux Conway a découvert une propriété du triangle qui aurait pu l’être par Euclide, trois siècles avant notre ère.
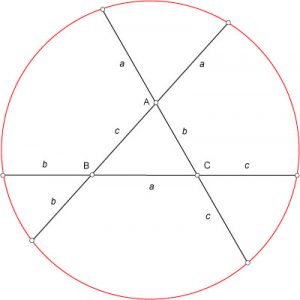
Soit ABC un triangle, a, b et c les longueurs des côtés BC, CA et AB. On prolonge les côtés comme indiqué sur la figure, on obtient ainsi six points notés de petits ronds sur la figure. Conway a découvert que ces six points appartenaient à un même cercle, appelé depuis cercle de Conway du triangle ABC en son honneur.
Analyse : centre du cercle de Conway
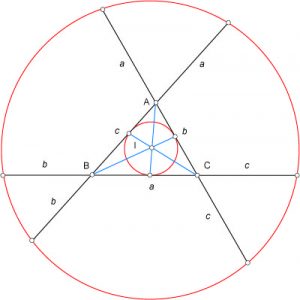
En supposant que ce cercle existe, on démontre en considérant les couples de points venant du même sommet que son centre appartient à chacune des bissectrices du triangle ABC. Il s’agit donc du centre du cercle inscrit I.
Synthèse : cercle de Conway
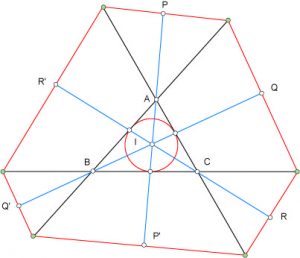
On considère les bissectrices PP’, QQ’ et RR’ du triangle ABC et le cercle de centre I passant par l’un des points verts. On démontre de proche en proche qu’il passe par tous les points verts puisque les droites PP’, QQ’ et RR’ sont les médiatrices des couples de points verts contigus.
Les coquilles des escargots sont des spirales qui peuvent croître de manière dextre ou senestre. En fait, ils sont presque tous dextres. Seuls un sur dix mille est senestre dans l’espèce des petits gris mais il existe des espèces où c’est le contraire.
Un petit gris. Si on place sa tête à gauche, sa coquille s’enroule dans le sens trigonométrique.
Les tire-bouchons usuels, c’est-à-dire pour droitiers, sont dextres, les tire-bouchons pour gauchers sont senestres.
Un tire-bouchon dextre.
Les queues de cochons
De même la queue en tire-bouchon des cochons peut être dextre ou senestre. Dans ce cas, il se trouve qu’il y a autant de cochons dextres que de cochons senestres. Le sexe des cochons mâles a la même propriété. Ces différences entre dextre et senestre se retrouvent au niveau des molécules, ce qui a parfois des conséquences sur leurs propriétés.
Le pangolin en boule
Pour échapper à ses prédateurs, le pangolin (oui, le mammifère impliqué dans l’origine du Covid-19) se roule en boule, ce qui le rend vulnérable aux braconniers.
Pangolin en boule
D’où la question : existe-t-il deux sortes de pangolins selon l’orientation de la boule ?
Hector Pétard, gendre du divin Bourbaki, mathématicien de génie, sut appliquer les transformations géométriques les plus abstraites à des domaines aussi concrets que la cynégétique.
La chasse au lion
Le lion est un animal constamment sur ses gardes. Comment l’attraper vivant sans éveiller ses soupçons ? Hector Pétard, illustre mathématicien du XXe siècle, apporta des réponses magistrales à ce problème. La principale concerne la géométrie.
L’idée géniale d’Hector Pétard pour chasser le lion sans danger est de disposer d’une cage dans laquelle il s’enferme seul. A l’instant initial, le lion est donc à l’extérieur. Il opère alors une transformation échangeant intérieur et extérieur de la cage. De ce fait, le lion se trouve dans la cage et lui à l’extérieur. L’idée générale étant trouvée, quelle cage et quelle transformation utiliser ?
L’étude des transformations géométriques donne la solution : la cage doit être sphérique et la transformation, une inversion, dont on comprend à ce propos le nom. Il s’agit d’inverser cage et monde extérieur !
La transformation qui à M associe M’ vérifiant : OM.OM’=R² échange extérieur (en vert) et intérieur (en orange) de la sphère de centre O et de rayon R.
Capture du lion
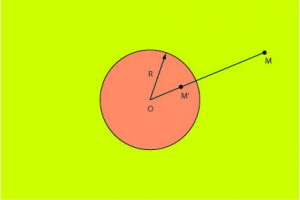
Prenez une inversion à effet limité afin d’éviter la surpopulation dans votre cage. Placez-la à proximité du lion, avec vous à l’intérieur. Opérez l’inversion. Vous vous trouvez à l’extérieur, et le lion à l’intérieur. Malgré la simplicité de la méthode, nous vous conseillons toutefois de l’essayer d’abord sur un chat domestique avant de vous lancer dans la chasse au lion. Je décline toute responsabilité en cas d’accident de chasse.
Cette méthode fait honneur à l’esprit mathématique le plus abstrait. Mais le génie d’Hector Pétard ne s’arrêtait pas là. Il sut imaginer des méthodes purement physiques, par exemple celle-ci que nous vous conseillons : un lion est de masse non nulle si bien qu’il a des moments d’inertie. Attendez l’un d’eux. Quand il se produira, vous n’aurez aucun mal à l’attraper !
L’humour mathématique
Ralph P. Boas (1912-1992), chasseur de lions
Cet article sur la chasse au lion est un exemple caractéristique d’humour mathématique. Celui-ci frise souvent l’absurde. Hector Pétard est le pseudonyme de Ralph P. Boas. Ses articles les plus cocasses ont été rassemblés par la Mathematical Association of America dans Lion hunting & other mathematical pursuits. Contemporain de la grande époque Bourbachique (1930-1960), il s’est imaginé converger en justes noces avec la fille du maître polycéphale. Son faire-part de mariage évoque ce temps béni des structures abstraites. Ma vocation de vulgarisateur des mathématiques est née de leurs dégâts collatéraux, quand leurs prosélytes ont créé un enseignement « moderne » des mathématiques, oubliant leurs applications. Nous dédions cette sonnerie aux morts à notre magistral chasseur de lions.
Faire-part de mariage de Betti Bourbaki
Monsieur NICOLAS BOURBAKI, Membre Canonique de l’Académie Royale de Poldévie, Grand Maître de l’Ordre des Compacts, Conservateur des Uniformes, Lord Protecteur des Filtres, et Madame, née BIUNIVOQUE, ont l’honneur de vous faire part du mariage de leur fille BETTI avec Monsieur HECTOR PETARD, Administrateur Délégué de la Société des Structures Induites, Membre Diplômé de l’Institute of Class Field Archeologist, secrétaire de l’Œuvre du Sou du Lion.
Monsieur ERSATZ STANISLAS PONDICZERY, Complexe de Recouvrement de Première Classe en retraite, Président du Home de Rééducation des Faiblement Convergents, Chevalier des Quatre U, Grand Opérateur du Groupe Hyperbolique, Knight of the Total Order of the Golden Mean, L.U.B., C.C., H.L.C., et Madame, née COMPACTENSOI, ont l’honneur de vous faire part du mariage de leur pupille HECTOR PETARD avec Mademoiselle BETTI BOURBAKI, ancienne élève des Bien Ordonnées de Besse.
L’isomorphisme trivial leur sera donné par le P. Adique, de l’Ordre des Diophantiens, en la Cohomologie principale de la variété universelle le 3 Cartembre, an VI, à l’heure habituelle.
L’orgue sera tenu par Monsieur Modulo, Assistant Simplexe de la Grassmannienne (lemme chanté par la Schola Cartanorum). Le produit de la quête sera versé intégralement à la maison de retraite des Pauvres Abstraits. La convergence sera assurée. Après la congruence, Monsieur et Madame BOURBAKI recevront dans leurs domaines fondamentaux. Sauterie avec le concours de la fanfare du 7e Corps Quotient. Tenue canonique (idéaux à gauche à la boutonnière)
Dans leurs calculs, les statisticiens utilisent la loi des grands nombres. La française des jeux n’opère pas autrement pour gagner de l’argent ! Le hasard n’intervient que pour les joueurs, pas pour elle ! Les compagnies d’assurance agissent de même. Si elles assurent cent mille voitures, elles savent d’avance combien auront d’accidents et quel en sera le coût. La prime d’assurance est calculée en fonction de ce risque qui n’en est plus un dès que l’on applique la loi des grands nombres ! Si 5% des automobilistes ont un accident chaque année, vous ne pouvez prévoir si vous en aurez un. En revanche, votre compagnie d’assurance sait que, sur ses cent mille assurés, cinq mille auront un accident.
La loi des petits nombres
Les particuliers ne raisonnent pas ainsi. Si un événement malheureux mais peu probable se produit deux fois de suite à une année d’intervalle, ils se diront que jamais deux sans trois et prévoiront un troisième pour l’année suivante. A l’inverse, plusieurs années sans accident leur feront croire que plus rien ne peut leur arriver. Autrement dit, ils utilisent une loi des petits nombres et non la loi des grands nombres. Bien entendu, il ne s’agit pas de mathématique mais de psychologie !
Une question de psychologie
Pour un mathématicien, cette loi des petits nombres peut passer pour un canular. C’est pourtant de manière tout à fait scientifique et en utilisant correctement la loi des grands nombres que Daniel Kahneman l’a mise en évidence. Plus précisément, il a étudié expérimentalement le comportement moyen des américains devant l’assurance ! Il apparaît que plusieurs années sans accident pousse la moyenne des américains à résilier ses contrats d’assurance ! Pour cette étude, ce professeur de psychologie à Princeton a obtenu le Prix Nobel d’économie en 2002.
Il semblerait que certains états appliquent cette loi des petits nombres et suppriment des équipements de précaution, comme des masques de protection, quand ils se sont révélés inutiles plusieurs années de suite. D’autres, dans l’affolement, feront des tests de médicaments sur des petits nombres pour en déduire avoir trouvé le traitement miracle.
Prenez un mot de neuf lettres, comme « minutieux », brouillez-les, vous obtenez par exemple XNIIMTUEU. Écrivez-le dans ce nouvel ordre dans un carré 3 par 3 :
Une grille de quatre sur neuf.
Nous avons ainsi formé une grille de notre jeu quatre sur neuf. Le but est maintenant de trouver un maximum de mots français de quatre lettres contenant la lettre centrale (en bleu, ici M) en un minimum de temps. Les accents ne comptent pas, ainsi mute et muté sont considérés comme le même mot.
Si on commence par les mots dont la première lettre est M, nous trouvons rapidement : mite, mine, mixe, mute, muni, muet, meut, etc. Nous pouvons continuer en essayant de placer M dans une autre position : émut, etc.
Quelle est la meilleure stratégie possible ? Chacun la sienne sans doute mais le jeu demande manifestement des qualités de lecture d’un pavé de trois lettres sur trois. Comment voir les chemins intéressants ? Il demande aussi de considérer les digrammes selon leurs fréquences. Par exemple, ici, « en » et « un » sont fréquents donc à considérer pour gagner du temps.
Combien existe-t-il de solutions pour cette grille ? La question est ouverte et la réponse dépend du dictionnaire utilisé. Peut-on trouver une grille sans solution ? Avec une seule ? Deux, etc. ? Toutes ces questions sont ouvertes cher lecteur… et attendent vos réponses. On comprendra, par exemple, que de partir d’un mot de neuf lettres assure la présence de lettres, digrammes et trigrammes relativement fréquents… et donc augmente le nombre de solutions.
Pour vous exercer
Il est facile de créer d’autres grilles, et de même de créer un logiciel pour jouer à ce jeu en français.
On part d’une liste de mots de neuf lettres (il en existe plus de 50 000), d’un générateur de permutations aléatoires d’un ensemble à neuf éléments puis d’un dictionnaire pour vérifier les solutions trouvées. Il reste à ajouter une horloge pour augmenter le stress du joueur. Attention avant de créer ce jeu : il est hautement addictif et son abus peut provoquer de graves ennuis de santé !
Le jeu de la vie, inventé en 1970 par John Conway, n’est pas vraiment un jeu. Ce terme est cependant moins rébarbatif que celui d’automate cellulaire, qui est pourtant plus exact. Il trouve ses origines dans des travaux conduits par John von Neumann dans les années 1940. Nous garderons la métaphore du jeu pour en parler, même si certains trouveront le terme mal adapté quand il s’agit de maladies potentiellement mortelles. L’essentiel est d’aider la compréhension. Voyons quelles en sont les règles.
Les règles du jeu de la vie
Pour jouer, prenez un damier et des pions. Les cases sont considérées comme des cellules ; elles peuvent être mortes ou vivantes. On utilise les pions pour matérialiser les cellules vivantes. Au début du jeu, on place des pions sur n’importe quelle case. On joue ensuite par étapes selon les règles suivantes :
— une cellule morte entourée de trois cellules vivantes ressuscite, sinon elle reste morte ;
— une cellule vivante reste en vie si elle a deux ou trois voisines vivantes, sinon elle meurt.
Bien que l’évolution du jeu soit complètement déterminée par la disposition initiale des cellules, on n’en assiste pas moins à quelques situations qui peuvent paraître surprenantes. Ainsi, en alignant tout simplement trois cellules vivantes les unes à côté des autres, on obtient une situation où les trois cellules se reproduisent, alignées horizontalement puis verticalement et ainsi de suite.
Lorsque trois cellules vivantes sont contiguës, on assiste à une oscillation entre trois cellules en ligne et trois en colonne.
Le jeu des épidémies
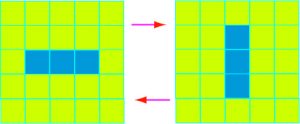
Ce jeu est loin d’être un simple amusement : il s’agit d’un exemple de ce que l’on nomme « automate cellulaire », particulièrement utile pour modéliser les processus d’expansion des épidémies comme des épizooties. En préalable à ce type d’application, il est nécessaire d’étendre le damier à l’infini. Au départ, toutes les cellules sont saines. On place une cellule infectée puis on « joue » avec la règle probabiliste suivante :
— les cellules voisines de la cellule infectée sont infectées au coup suivant avec la probabilité p ;
— la cellule meurt ou est immunisée le coup suivant.
Comment les cellules infectées (en rouge) se multiplient-elles au détriment des cellules saines (en vert) ? Dans cet exemple, la probabilité qu’une cellule voisine d’une cellule infectée soit infectée à son tour est de 25 %. Les cellules mortes ou immunisées sont représentées en bleu.
La question qui intéresse autant les épidémiologistes que le grand public est donc : « Pour quelles valeurs de p, la maladie se propage-t-elle au monde entier ? »
Un modèle probabiliste
Le modèle est ici « probabiliste », et donc on ne peut prédire à l’avance ce qui va se produire dans un cas particulier. Pour avoir une idée rapide de l’évolution moyenne du système, le mieux est de procéder à une simulation. Pour cela, on « joue » selon les règles énoncées ci-dessus en utilisant un générateur de nombres pseudo-aléatoires et on comptabilise le nombre de cellules infectées. En jouant cent fois de suite et en faisant la moyenne des résultats, on obtient une mesure de l’expansion moyenne de l’épidémie.
Taux critique
En dessous d’un certain taux de contamination p, l’épidémie ne s’étend pas. En revanche, au dessus de ce taux, elle envahit le monde entier. Dans le cadre de notre modèle simplifié, le taux critique se situe entre 30 % et 40 %. Une maladie ne devient épidémique que si ce taux est dépassé. Comment ce modèle peut-il être adapté pour bien modéliser différents types d’épidémies ou d’épizooties ? Tout d’abord, on peut modifier le voisinage de chaque cellule, composé ici de huit cellules — les spécialistes parlent de voisinage de Moore, du nom d’Edward Moore, l’un des fondateurs de la théorie des automates. On utilise souvent un voisinage plus simple, dit de von Neumann, constitué des quatre cellules partageant un côté avec la cellule considérée. Avec ce nouveau modèle, le taux critique pour lequel une maladie devient épidémique se situe aux alentours de 60 %. On peut également améliorer le modèle en tenant compte du temps pendant lequel une cellule infectée est contagieuse puis du taux de mortalité et d’immunité ainsi que du temps d’immunité. On arrive ainsi à retrouver la façon dont se sont propagées des épidémies comme la peste dans l’Europe médiévale. Une première vague a tué le tiers de la population en se propageant à partir d’un épicentre situé dans un port, suivie de plusieurs répliques plus faibles, toutes partant du même point. Ces répliques correspondent à la fin de certaines immunités.
La confrontation avec les données épidémiologiques a permis de montrer que ce type de modèles a une certaine pertinence pour toutes les maladies qui se propagent par contact direct : grippe, tuberculose, coronavirus ou même sida. En revanche, il ne fonctionne plus lorsque la maladie se propage via un agent infectieux, comme dans le cas du paludisme ou du chikungunya.
Géométrie des contagions
Comment considérer maintenant la notion de « cellule voisine » dès que l’on évoque les réseaux de transports aériens, maritimes ou terrestres ? Dans le cas d’une épidémie de grippe humaine, l’aéroport de Paris est voisin de celui de Hong-Kong. Dans le cas d’une épizootie de grippe aviaire, deux élevages fréquentant le même marché aux bestiaux sont voisins. On doit de plus tenir compte des migrations naturelles des oiseaux sauvages. Dans tous ces cas, on retrouve la notion de réseaux.
En modifiant le modèle du jeu, on peut passer du cas où chaque cellule représente un individu à celui où elle représente un domaine où les individus sont en relation constante : un élevage de volaille dans le cas de la grippe aviaire, une ville dans le cas de la tuberculose, du sida ou de la grippe humaine. Ces domaines sont reliés entre eux pour former un réseau. Dans chaque cellule, la modélisation suit une autre logique, celle du modèle « SIR » dû à William Kermack et Anderson Mac Kendrick en 1927 (voir l’article correspondant sur ce blog). Ce modèle compartimente la population en trois classes : S, la classe des individus susceptibles d’attraper la maladie, I, celle de ceux qui en sont infectés (et contagieuses) et R, ceux qui en sont guéris (et immunisés) ou décédés.
Seuil de propagation
On considère l’évolution de ces trois classes dans le temps en fonction de deux taux mesurables expérimentalement. Le premier (a) est le taux de contagion de la maladie pour un infecté, c’est-à-dire la probabilité pour qu’un individu susceptible attrape la maladie après contact avec un individu infecté. Le second taux (b) mesure le passage de l’état I à l’état R.
Après un laps de temps t, on compte aI S t infectés supplémentaires et R augmente de bI t. La variation du nombre d’infectés est donc égale à aS – b multiplié par I t. La condition pour que la maladie se propage (et donc donne lieu à une épidémie) est que le nombre de malades infectés augmente, c’est-à-dire que : aS – b > 0. Le quotient b / a a donc valeur de seuil. Si le nombre de sujets susceptibles est strictement inférieur à ce seuil, la maladie ne s’étend pas. Sinon, elle donne lieu à une épidémie (ou à une épizootie).
D’une façon qui peut paraître paradoxale, l’apparition d’une épidémie ne dépend donc pas du nombre de personnes infectées mais du nombre de personnes susceptibles d’attraper la maladie ! Cette remarque justifie à elle seule les politiques de vaccination, même avec un vaccin peu efficace.
Dans Les Eléments, Euclide pose plusieurs axiomes et définitions de la géométrie plane puis démontre un certain nombre de théorèmes. Entre les deux, il postule que, par un point donné, il passe une et une seule parallèle à une droite donnée. En apparence, il s’agit d’un théorème sans preuve. Des générations de mathématiciens ont essayé de le démontrer sans jamais y arriver. Avant d’analyser la question, il est nécessaire de revenir sur les axiomes d’Euclide.
Les axiomes d’Euclide
Il serait fastidieux de passer en revue les axiomes et les définitions de la géométrie plane d’Euclide. Pour en comprendre l’origine, il suffit de revenir au mythe de la caverne, une allégorie où Platon estime que le monde réel est rempli d’objets dont les modèles sont ailleurs, dans le monde des idées. De la même façon, les points, droites et angles d’Euclide sont les idées des points, droites et angles réels tels qu’un maçon les utilise. Qu’est-ce qu’une droite ? Pour le comprendre, faites comme le maçon. Prenez une corde et deux piquets. Plantez les deux piquets et tendez la corde. Vous réalisez ainsi le plus court chemin entre eux.
En tendant une corde entre deux piquets, on obtient une droite.
Avec la même méthode et trois piquets, vous fabriquez un triangle donc trois angles.
En tendant une corde entre trois piquets, on obtient un triangle Mesurez les angles et faites-en la somme. Comme vous connaissez déjà le résultat, vous trouverez 180°.
Une preuve sous condition
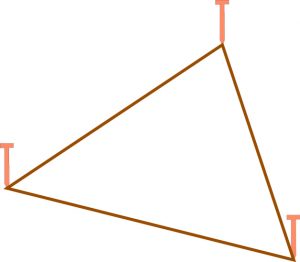
Une petite figure suffit pour démontrer ce résultat. Pour la tracer, en plus de notre corde et de nos piquets, munissons-nous d’un rapporteur capable de reporter un angle donné le long d’une droite, en un point.
Considérez un triangle ABC, prolongez le côté AB en BE et du point B, en utilisant le rapporteur, portez la droite BD de sorte que l’angle CBD soit égal à l’angle ACB (en rouge tous les deux). De même, portez la droite BD’ de façon que l’angle EBD’ soit égal à l’angle BAC (en bleu).
En B, on reporte les angles en rouge et en bleu, on obtient deux droites BD et BD’. D’après le postulat d’Euclide, ces droites sont confondues. Les angles du triangle ABC se retrouvent donc en B et forment un angle plat c’est-à-dire 180°.
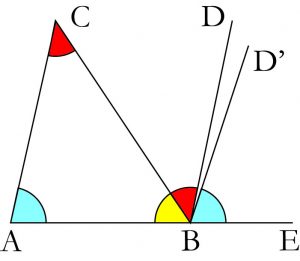
Les droites BD et BD’ sont parallèles à la droite AC (les angles rouges et jaunes sont alternes internes). Elles sont donc identiques puisque, d’un point, on ne peut tracer qu’une parallèle à une droite donnée. Les trois angles du triangle ABC se reportent ainsi en B pour former un angle plat, c’est-à-dire 180°. Nous avons ainsi démontré que la somme des angles d’un triangle est égale à 180° … si le postulat d’Euclide est vrai.
L’idée qui dépostule
Quand on dessine la figure précédente sur une feuille de papier, les droites BD et BD’ sont confondues. Coupons le papier le long de la demi-droite BD et déplaçons BD’ sur BD, la feuille se courbe. Elle devient comme un sommet de montagne et la somme des angles du triangle, supérieure à 180°. Au contraire, en écartant BD’ de BD, la feuille se courbe dans l’autre sens. Elle devient comme un col de montagne et la somme des angles du triangle, inférieure à 180°.
Triangle sur la sphère
Pour développer cette idée, reprenons les axiomes d’Euclide sans le postulat en nous plaçant avec nos piquets, notre corde, notre rapporteur et nos définitions sur une sphère. Le plus court chemin entre deux points est obtenu en suivant l’arc de grand cercle entre eux.
Ligne droite sur une sphère.
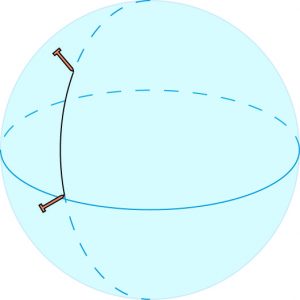
Sur une sphère, deux grands cercles se coupent toujours. Autrement dit, deux droites ne sont jamais parallèles ! Le postulat d’Euclide y est faux et notre démonstration lumineuse aussi. Dans ce cas, les deux droites BD et BD’ ne se recoupent pas, l’angle DBD’ n’est pas nul. La somme des angles du triangle est donc supérieure à 180°. Pour vous en convaincre davantage, prenez un globe terrestre miniature, deux points sur l’équateur et dessinez le triangle formé avec l’un des pôles. La somme de ses angles est égale à 180° plus l’angle au pôle, elle est donc strictement supérieure à 180°.
Triangle sur une sphère. En mesurant ses angles, on montre que leur somme est supérieure à 180°.
Triangle sur une selle de cheval
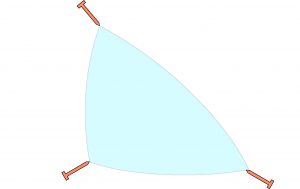
Si nous nous plaçons sur une surface différente comme un col de montagne ou une selle de cheval, la somme des angles d’un triangle devient inférieure à 180°. Sur la figure de notre démonstration, les droites BD et BD’ se couvrent.
Un triangle sur une selle de cheval.
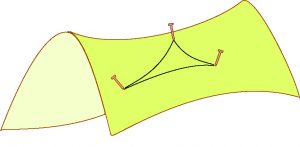
Les surfaces comme les plans, les cylindres ou les cônes où la somme des angles d’un triangle est égale à 180° sont dites de courbure nulle, celles comme la sphère ou les ellipsoïdes où la somme des angles est supérieure à 180°, de courbure positive et celles comme la selle de cheval où la somme des angles est inférieure à 180°, de courbure négative. Ces surfaces ne sont pas des plans euclidiens.
Aire d’un cercle
De même, grâce à un piquet et une corde, sur toute surface, nous pouvons tracer un cercle de rayon R. Si la courbure de la surface est nulle, son aire est égale à p R2. Si elle positive, elle est inférieure, sinon elle est supérieure.
Courbure d’un espace
Notre vision en trois dimensions nous permet d’admettre facilement ces résultats. Imaginons des êtres plats « collés » sur une surface de dimension deux pour lesquels, elle serait l’univers entier. Incapable d’en sortir, il ne verrait pas sa courbure. Il pourrait cependant tracer un triangle, mesurer ses angles et déterminer ainsi si son univers a une courbure positive, négative ou nulle.
De même, un extraterrestre vivant et voyant dans un monde en dimension quatre pourrait « voir » la courbure de notre univers. Nous y sommes trop englués pour cela. Le même phénomène existe pourtant et nous pouvons le tester : il suffit de mesurer le volume d’une sphère ou la somme des angles d’un triangle. Jusqu’à présent, les mesures effectuées font penser que notre univers est de courbure quasiment nulle.
Certaines croyances magiques restent attachées aux mathématiques. L’exemple le plus simple est celui du nombre treize qui porte chance … ou malchance selon les personnes. On évite ainsi, même chez certains mathématiciens, d’être treize à table. Cette croyance est extra-mathématique. Elle vient du dernier repas du Christ avec ses apôtres et non pas d’une propriété mathématique du nombre treize. Il en est de même de la plupart des nombres considérés comme magiques ou sacrés, comme sept par exemple. Nous n’insisterons pas sur cette question, et pas davantage sur la numérologie ou sur l’arithmancie qui prétendent prévoir l’avenir au travers de quelques additions. Leurs relations aux mathématiques sont les mêmes que celle de l’astrologie à l’astronomie. Même si certains mathématiciens furent numérologues comme certains astronomes furent astrologues jusqu’à l’époque de Kepler (XVIIe siècle), aujourd’hui, il est difficilement imaginable qu’un mathématicien ou un astronome pratique ce type de pseudosciences.
Les nombres parfaits
Plus étonnants que ces nombres auxquels on attribue un pouvoir surnaturel, d’autres sont considérés comme magiques pour des raisons internes aux mathématiques. Parmi les plus étudiés sont les nombres parfaits dont parle déjà Euclide au IIIe siècle avant notre ère dans ses Éléments. Par définition, les nombres parfaits sont les nombres égaux à la somme de leurs diviseurs autres qu’eux-mêmes. Par exemple, 6 est parfait puisque ses diviseurs stricts sont 1, 2 et 3 dont la somme est égale à 6. La traduction littérale du terme grec utilisé par Euclide pour désigner les nombres parfaits est nombre à qui il ne manque rien ce qui permet de mieux comprendre les définitions de nombre abondant et de nombre déficient : nombre dont la somme des diviseurs est supérieure (respectivement inférieure) au nombre donné. Ainsi 12 est abondant, 3, 4 et 5 sont déficients.
Quand Dieu est contraint à la perfection …
Saint Augustin (354 – 430) d’après un tableau de la Renaissance
Cela pourrait être une simple curiosité et peu importe le nom utilisé mais, dans l’Antiquité, la perfection de ces nombres était bien vue comme telle. Ainsi, dans La cité de Dieu, on peut lire sous la plume d’Augustin d’Hippone (354 – 430) une vision mystique de cette perfection : Ainsi, nous ne devons pas dire que le nombre six est parfait, parce que Dieu a achevé tous ses ouvrages en six jours : loin de là, Dieu a achevé tous ses ouvrages en six jours parce que le nombre six est parfait ; supprimez le monde, ce nombre resterait également parfait ; mais s’il n’était pas parfait, le monde, qui reproduit les mêmes rapports, n’aurait plus la même perfection.
On trouve des idées voisines dans Arithmetica d’un philosophe néo-pythagoricien comme Nicomaque de Gérase (Ier siècle de notre ère), pourtant véritable mathématicien puisqu’il découvrit le quatrième nombre parfait : Il arrive que, de même que le beau et le parfait sont rares et se comptent aisément, tandis que le laid et le mauvais sont prolifiques, les nombres excédents et déficients sont en très grand nombre et en grand désordre ; leur découverte manque de toute logique. Au contraire, les nombres parfaits se comptent facilement et se succèdent dans un ordre convenable ; on n’en trouve qu’un seul parmi les unités, 6, un seul dans les dizaines, 28, un troisième assez loin dans les centaines, 496 ; quant au quatrième, dans le domaine des mille, il est voisin de dix mille, c’est 8128. Ils ont un caractère commun, c’est de se terminer par un 6 ou par un 8, et ils sont tous invariablement pairs.
Des conjectures à la pelle
À l’heure actuelle, le dernier point évoqué par Nicomaque de Gérase reste une conjecture. Personne n’a encore réussi à prouver qu’il n’existait pas de nombres parfaits impairs, même si le fait que personne n’en ait jamais trouvé un seul milite dans ce sens. De même, l’existence d’une infinité de nombres parfaits pairs est une conjecture. Les quatre premiers sont connus depuis l’Antiquité : 6, 28, 496 et 8128 et, à l’heure actuelle, nous n’en connaissons que 49 ! Les plus grands n’ont été découverts que récemment et ont plusieurs dizaines de millions de chiffres. Ils sont tous d’une forme liée à la notion de nombre premier, ce que nous verrons plus loin.
Les temps ont changé et plus personne ne comprend l’expression « nombre parfait » dans le sens d’une perfection externe aux mathématiques.
Comment comprendre le monde moderne sans culture mathématique ? Accéder à celle-ci n’exige cependant pas d’apprendre à résoudre la moindre équation.
