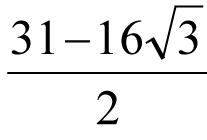Traditionnellement, chaque groupe, professionnel ou autre, a son saint patron. Ce saint a en général un lien avec le groupe en question.
Gabriel, saint patron des transmetteurs

Par exemple, le saint patron des transmetteurs de l’armée est très logiquement l’archange Gabriel, celui qui annonce les bonnes nouvelles comme celle faite à Marie dans les Évangiles. La fête des transmetteurs est donc le 29 septembre, le jour de la saint Gabriel. Le saint patron du renseignement militaire est un autre archange, Raphaël, fêté le même jour comme tous les archanges. La relation de ce saint avec le renseignement est mystérieuse. Saint Simon nous aurait semblé plus approprié, lui qui fut qualifié d’espion sagace et fantasque de Versailles et des coulisses du pouvoir au temps de Louis XIV par l’académicien Yves Coirault (1919 – 2001). Même si nous penchons nettement en faveur du choix de saint Simon, comme saint patron des espions, nous respectons la tradition qui lui préfère Raphaël.
L’évidence de Saint Urlo
En ce qui concerne les cryptologues, d’après leur proximité avec les transmissions et le renseignement, ils peuvent se réclamer de Gabriel, de Raphaël et de saint Simon, mais ils préfèrent souvent reconnaître le patronage de saint Urlo. Pourquoi ? Toux ceux qui se sont déjà attaqués au décryptement de vieux grimoires écrits avec des alphabets chiffrés le savent. La lettre la plus fréquente en français est la lettre e, ensuite viennent dans un ordre approximatif s, a, i, n, t, u, r, l, o. Affirmer qu’Urlo est le saint patron des cryptologues est une bonne façon de se souvenir des lettres les plus fréquentes en français, pour appliquer l’analyse fréquentielle.
Un saint breton qui a sa chapelle

Notre présentation d’Urlo peut faire penser qu’il s’agit d’un saint imaginaire. Pourtant un voyage dans le Morbihan, à Lanvévégen plus précisément, vous le fera découvrir. En effet, il s’agit d’un saint breton. L’orthographe de son nom varie de Gurloës à Ourlou en passant par Urlo. Au XIe siècle, Urlo fut le premier abbé de l’abbaye Sainte-Croix de Quimperlé. Il ne fut canonisé que difficilement car personne n’avait été témoin d’un seul miracle qu’il aurait réalisé. Pour nous, cela n’est qu’une preuve supplémentaire de son lien avec la cryptologie car les exploits des décrypteurs sont effectivement tenus secrets longtemps. La fête de saint Urlo est le 25 mars.











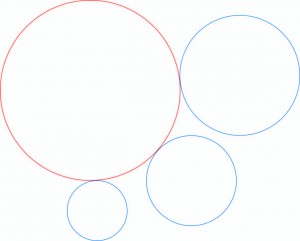


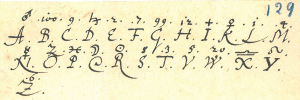


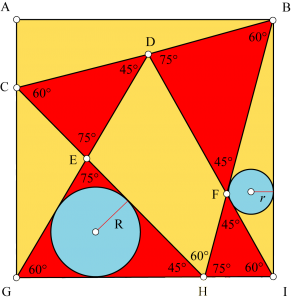
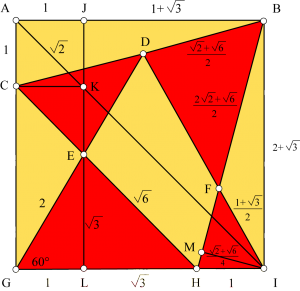
 Les deux triangles (rouge et vert) inscrits dans le carré jaune sont équilatéraux, quel est le rapport entre les rayons des cercles bleus ?
Les deux triangles (rouge et vert) inscrits dans le carré jaune sont équilatéraux, quel est le rapport entre les rayons des cercles bleus ?