Pythagore pensait que tout était nombre, nombre entier plus précisément ou rapport de nombres entiers. De nos jours, on dit nombres rationnels, du latin ratio qui, dans ce contexte signifie rapport.
La duplication du carré
Dans le Ménon de Platon, le problème de Socrate est celui de la duplication du carré, c’est-à-dire de trouver un carré d’aire double d’un carré donné.
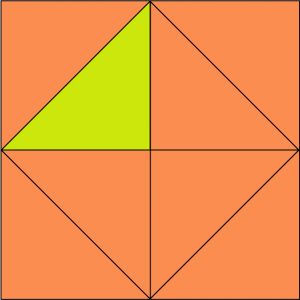
La solution pour dupliquer un carré est d’en construire un dont le côté est la diagonale du premier. Selon le théorème de Pythagore, d 2 = 2 a 2 où a est le côté du carré et d sa diagonale. Si tout est nombre, a et d sont deux nombres entiers naturels (en choisissant bien l’unité).
Un raisonnement par l’absurde
Ici commence un raisonnement mathématique subtil, l’un des plus anciens de ce type. Bien que nous ne connaissions aucun de ces deux nombres, nous imaginons la factorisation de d 2 = 2 a 2 et y comptons les occurrences du facteur 2 en utilisant chacune des formes à droite et à gauche du signe égal. Ce nombre est pair dans d 2 puisque chaque apparition dans d est doublée par l’effet de la multiplication par lui-même. Le même phénomène se produit dans a 2. En multipliant cette quantité par 2, on en ajoute un. Le nombre de 2 dans 2 a 2 est donc impair. L’égalité d 2 = 2 a 2 conduit à une absurdité : le nombre de 2 est à la fois pair (dans d 2) et impair (dans 2 a 2). L’hypothèse de l’existence d’une commune mesure entre les côtés des deux carrés aboutit à une absurdité, elle est donc fausse.
L’écroulement du dogme de Pythagore
L’idée de Pythagore s’écroule, il existe des longueurs incommensurables. Son dogme « tout est nombre » ne retrouvera vie que dans les temps modernes, quand d’autres « objets » seront admis dans le champ des nombres, en particulier, le rapport de la diagonale au côté du carré, racine de 2 que nous disons irrationnel, non pas parce que ce nombre ne serait pas raisonnable mais parce qu’il ne s’agit pas d’un rapport d’entiers.
