La quadrature du cercle consiste à construire un carré de même aire qu’un cercle donné. Si le cercle a pour rayon R, il s’agit donc de construire un carré de côté R multiplié par la racine carrée du nombre Pi. On peut donc réaliser la quadrature du cercle avec une règle graduée à la précision que l’on veut.
Des règles qui changent tout
Quand le problème est apparu dans l’Antiquité, il n’était pas question d’approximations, la règle était que la construction devait être exacte. Il en existe plusieurs. L’une d’entre elle demande de faire rouler un cercle sur une droite. La voici sous forme de tableau :
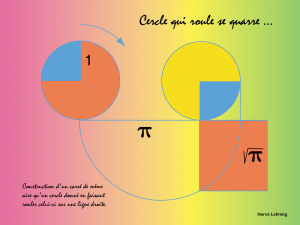
En utilisant uniquement le théorème de Pythagore, on démontre que le carré est de côté racine de Pi, ce qui prouve que le carré et le cercle ont même aire (voir à la fin pour une démonstration).
Cette utilisation d’un procédé mécanique (faire rouler le cercle) ne convenait pas aux anciens, il fallait construire le carré à la règle (non graduée) et au compas. Dans ces conditions, le problème devient impossible, ce qui n’a été prouvé qu’au XIX-ième siècle en démontrant que le nombre Pi est transcendant c’est-à-dire qu’il n’est pas solution d’une équation algébrique à coefficients entiers.
De façon étonnante, un problème purement géométrique et très conditionné par des visions antiques a eu des conséquences importantes en algèbre et en analyse.
Un peu de géométrie
La figure essentielle est la suivante :
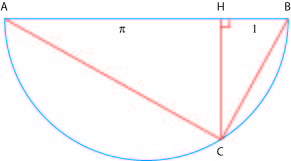
En appliquant le théorème de Pythagore dans les trois triangles rectangles HBC, HC et ABC, on obtient :
HC² + 1 = BC², HC²+ Pi² = AC² et BC² + AC² = (Pi + 1)²
En faisant la somme des deux premières expressions puis un peu d’algèbre, il vient que HC² est égal à Pi ce qu’il fallait démontrer.
Une lampe pour une idée lumineuse
Cette quadrature du cercle, dont l’auteur initial nous est inconnu, m’a inspiré la lampe suivant :

