Selon les écrits de Gustave Eiffel, la forme de sa tour ne doit rien au hasard, même si le résultat pourrait plaider pour un simple souci d’esthétique. Selon lui, tout a été étudié mathématiquement pour résister au vent. Plus précisément, il affirme que le moment des forces appliquées par le vent en chaque point est égal et opposé au moment du poids de la structure en ce point. Les calculs mathématiques d’Eiffel n’ayant pas été publiés, on a longtemps soupçonné les ingénieurs d’Eiffel d’avoir opéré empiriquement pour obtenir la forme de type exponentiel qu’on connaît.

Reconstitution des calculs

Les calculs ont été repris en 2005 par deux mathématiciens américains, Patrick Weidman et Iosif Pinelis. En suivant les indications d’Eiffel, ils ont débouché sur une équation intégro-différentielle relativement simple … pour les spécialistes … dont la solution est bien une exponentielle.

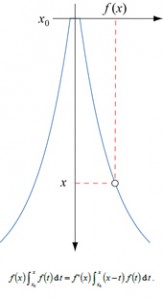
Mais, en réalité, la tour Eiffel est composée de deux exponentielles pour tenir compte de la différence de forces du vent à la base et au sommet.