Les Cosmosaïques sont une série de collages que j’ai réalisés à partir de 2005, suite à une longue réflexion sur la notion de symétrie et de brisure de symétrie ainsi que de mes travaux sur la topologie cosmique et les pavages d’espace. L’idée fondatrice est qu’en physique tout comme dans les arts, la symétrie parfaite est statique, tandis que les brisures de symétrie engendrent la dynamique.

Tout au long de l’histoire, de nombreux penseurs ont été si imprégnés d’un certain sentiment de la symétrie qu’ils n’ont pu s’empêcher de croire qu’elle tient une place importante dans l’explication du monde. Dans son texte Eurêka (1848), Edgar Poe écrivait  : “Le sentiment de la symétrie est un instinct qui repose sur une confiance presque aveugle. C’est l’essence poétique de l’univers, de cet Univers qui, dans la perfection de sa symétrie, est simplement le plus sublime des poèmes. Or, symétrie et cohérence sont des termes réciproquement convertibles ; ainsi la Poésie et la Vérité ne font qu’un…”

De fait, la notion de symétrie fascine scientifiques et artistes depuis l’Antiquité, et d’innombrables œuvres et ouvrages lui sont consacrés. Aujourd’hui encore, la symétrie traverse la totalité du champ de la physique, au point d’en devenir le pilier fondateur.

Par exemple, depuis trente ans, les chercheurs tentent d’unifier les forces et les particules qui constituent notre univers matériel, c’est-à-dire leur trouver une description mathématique commune. Une telle « superthéorie » rendrait compte non seulement de toutes les formes connues et inconnues de la matière, mais aussi des quatre interactions fondamentales que sont la gravitation, l’électromagnétisme, les interactions nucléaires forte et faible. Ces théories d’unification sont encore variées : Grande Unification, supersymétrie, supercordes, etc., mais leur hypothèse de base commune est que la nature opère selon un ensemble de règles mathématiques se ramenant à des symétries. Bien que les symétries de la nature soient aujourd’hui cachées dans notre Univers à basse énergie, elles se révèleraient à très haute température et peuvent être étudiées dans les accélérateurs de particules.

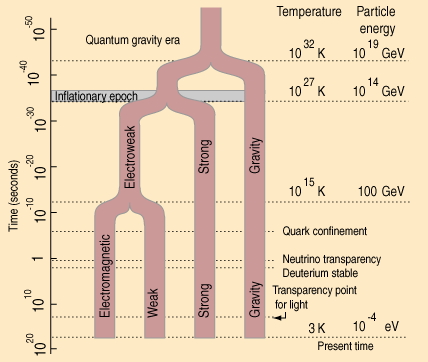
Cependant, plus fascinante encore est la notion de « brisure de symétrie ». En effet, le but réel des théories d’unification est double : il s’agit non seulement de découvrir les symétries sous-jacentes de l’Univers primitif (à très haute température), mais aussi de trouver des mécanismes physiques capables de « briser » ces symétries lorsque, au cours de son expansion, l’Univers est descendu à basse énergie. Après tout, nous vivons dans un Univers devenu complexe, empli de particules et d’interactions si diverses qu’elles se prêtent mal à une description trop symétrique. La complexité du monde peut donc se traduire par des écarts à la symétrie parfaite. La physique étudie précisément les brisures de symétrie et montre que celles-ci jouent un rôle au moins aussi fondamental dans la nature que les symétries en elles-mêmes. Un autre exemple frappant illustrant la richesse du concept se trouve en théorie des cordes, où les brisures de symétrie du vide quantique engendrent une multiplicité d’univers aux caractéristiques généralement différentes du nôtre, lequel ne serait donc qu’une réalisation hautement improbable au sein d’un « multivers ».

Il est remarquable que cette démarche se retrouve dans l’art et l’esthétique. La symétrie y est omniprésente, mais la notion (subjective) de « beauté » est davantage liée à un léger écart à la symétrie plutôt qu’à la symétrie parfaite. Les plus beaux visages ne sont pas exactement symétriques, les architectures les plus réussies mêlent symétrie et surprise… Continuer la lecture →