Je voudrais poser une question à monsieur Einstein, à savoir, à quelle vitesse l’action de la gravitation se propage-t-elle dans votre théorie ?
Max Born, 1913
Dans la théorie de Newton, la gravitation est une force agissant instantanément entre les corps massifs. Cette idée était inadmissible aux yeux de nombreux physiciens, Newton compris, et un siècle plus tard Laplace proposait une modification de la théorie dans laquelle l’interaction gravitationnelle se propageait à vitesse finie. L’idée fut vite abandonnée, car elle soulevait immédiatement une question à laquelle personne ne savait répondre : lorsqu’un corps massif est violemment perturbé, le champ gravitationnel qu’il engendre doit s’ajuster de proche en proche à la nouvelle configuration du corps ; sous quelle forme se propage le réajustement ?
La théorie de la relativité générale d’Einstein permet d’organiser en un schéma cohérent les intuitions sur la propagation de la gravitation. Einstein s’était demandé si une masse en mouvement accéléré pouvait rayonner des ondes de gravité, de la même façon qu’une charge électrique en mouvement accéléré rayonne des ondes électromagnétiques. Dès 1916, il découvrit effectivement des solutions de ses équations du champ gravitationnel représentant des ondulations de la courbure de l’espace-temps se propageant à la vitesse de la lumière. Il venait d’inventer la “lumière gravitationnelle”.
Good Vibrations
Et quel vent d’outre-monde emporte au gré des ondes
la promesse de toutes les germinations?
Charles Dobzynski
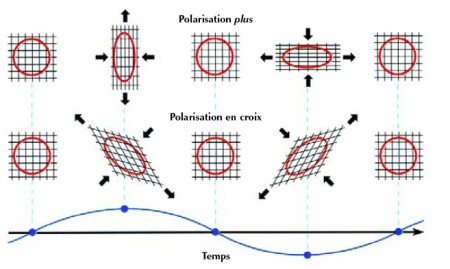
L’analogie entre ondes gravitationnelles et ondes électromagnétiques est utile pour la conception du phénomène, mais elle ne conduit guère plus loin. La structure d’une onde gravitationnelle et ses effets sur la matière sont bien plus complexes que ceux de l’onde électromagnétique. Une première différence notable vient du fait que la gravitation est purement attractive ; la masse, c’est-à-dire la « charge gravitationnelle », a toujours le même signe. Il en résulte qu’un oscillateur gravitationnel élémentaire, constitué de deux masses vibrant aux extrémités d’un ressort, ne rayonne pas le même type d’ondes que deux charges électriques de signe opposé. Dans le cas électromagnétique, le rayonnement est du type dipolaire, dans le cas gravitationnel il est du type quadripolaire.
Une autre complication vient de ce que le graviton, l’hypothétique particule médiatrice de l’onde gravitationnelle, transporte une charge gravitationnelle associée à son énergie, tandis que le photon, particule médiatrice de l’interaction électromagnétique, ne transporte pas de charge électrique. Par conséquent, l’onde de gravitation produite par une masse accélérée est elle-même source de gravitation : la gravitation gravite. En termes techniques, on dit qu’elle est non linéaire. Cette non-linéarité introduit des difficultés considérables dans la résolution des problèmes apparemment les plus simples, comme le calcul du champ gravitationnel engendré par deux corps en mouvement. Contrairement au champ électromagnétique, ou à la force de gravitation newtonienne, si deux masses produisent individuellement deux champs, leur action combinée produit un champ qui n’est pas la somme des deux champs ; il faut en plus tenir compte de la gravitation d’interaction entre les deux masses, qui varie constamment au cours du mouvement. C’est la raison pour laquelle le « problème à deux corps », décrivant par exemple le champ gravitationnel d’une étoile double et qui, dans la théorie de Newton, a une solution facile à calculer – en l’occurrence, les lois de Kepler – n’est pas résolu rigoureusement en relativité générale.
Toutefois, dans les champs gravitationnels suffisamment faibles, la non-linéarité peut être négligée et nombre de complications disparaissent. C’est justement le cas lorsqu’on s’intéresse à la détection du rayonnement gravitationnel en provenance de sources lointaines. Mais une telle simplification donnerait des résultats complètement erronés à proximité d’une supernova ou de deux trous noirs en collision…
La troisième différence fondamentale avec l’électromagnétisme réside dans leurs intensités relatives. Si l’on place à 1 centimètre l’un de l’autre deux protons – qui, ayant une masse et une charge électrique, sont à la fois soumis à une interaction gravitationnelle et à une interaction électromagnétique –, la force gravitationnelle qui les attire est 1037 fois plus faible que la force électrostatique qui les fait se repousser. De là vient l’obstacle majeur à la détection des ondes gravitationnelles ; alors qu’il a suffi d’une décennie après la prédiction de Maxwell pour que Hertz parvienne à produire et à capter en laboratoire des ondes électromagnétiques, un siècle sans résultat s’est écoulé après la prédiction d’Einstein.
Quelques exemples illustreront mieux l’extraordinaire faiblesse des ondes gravitationnelles dans les conditions usuelles. Revenons à notre oscillateur gravitationnel élémentaire, constitué de deux masses de 1 kilogramme oscillant de 1 centimètre 100 fois par seconde aux extrémités d’un ressort long de 10 centimètres. En admettant que l’on puisse recueillir toute la puissance gravitationnelle libérée par ce système et la convertir en puissance électrique, on peut calculer que, pour alimenter une seule ampoule de 50 watts, il faudrait autant d’oscillateurs que le nombre de particules contenu dans la planète !
Une façon équivalente de construire un oscillateur gravitationnel est de faire tourner une barre horizontale autour d’un axe vertical passant par son milieu. Lorsqu’on regarde la barre dans son plan de rotation, elle semble se contracter quand elle présente l’une de ses extrémités et se dilater lorsqu’elle se présente dans toute sa longueur. Elle engendre donc des ondes gravitationnelles. Prenons une barre d’acier de 20 mètres de long, pesant 500 tonnes, et faisons-la tourner à la limite de rupture, soit 5 tours par seconde. La puissance gravitationnelle libérée est encore ridicule : 10–29 watt.
Mieux vaut quitter le laboratoire et chercher des sources naturelles d’ondes gravitationnelles parmi les corps du système solaire. La situation n’est guère plus encourageante : il faudrait cinquante milliards de météores de 1 km de diamètre percutant la Terre à 10 km/s pour allumer la modeste ampoule électrique… et il n’y aurait plus personne pour la voir briller !
Il est vain de chercher les sources dans des corps astronomiques ordinaires. Pour engendrer des ondes gravitationnelles qui ne soient pas totalement insignifiantes, l’astre générateur doit se déplacer à une vitesse proche de celle de la lumière et être compact, c’est-à-dire proche de son rayon de Schwarzschild. La Terre, qui tourne autour du Soleil à la vitesse de 30 km/s et dont le rayon est un milliard de fois plus grand que son rayon de Schwarzschild, n’engendre qu’une puissance gravitationnelle d’un dix millième de watt.
Or, on connaît des astres “relativistes”, pouvant réunir au moins temporairement les conditions favorables à l’émission de lumière gravitationnelle. Seuls les sites astronomiques les plus violents sont de bons générateurs d’ondes gravitationnelles. Comme les astres violents sont très lointains (heureusement pour nous, car si un cataclysme astronomique se produisait à proximité de la Terre, il n’y aurait tout simplement plus de vie), ils ne déposent sur notre planète qu’une minuscule fraction de leur énergie gravitationnelle.
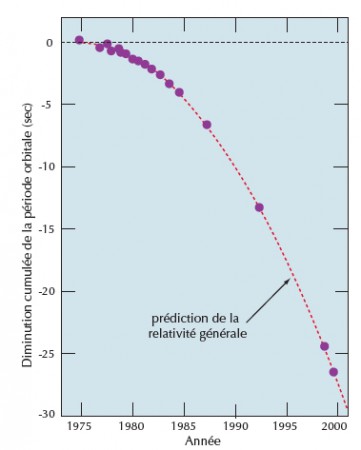
Les systèmes d’étoiles compactes sont de bons générateurs d’ondes gravitationnelles. Un couple serré d’étoiles à neutrons rayonne suffisamment d’énergie gravitationnelle pour que les effets soient détectables, bien que sous une forme indirecte : la perte d’énergie orbitale se traduit par une diminution de la période de révolution. Le pulsar binaire PSR 1913+16 est une parfaite illustration du phénomène ; lui et ses homologues ont offert la première démonstration expérimentale de l’existence des ondes gravitationnelles – ce qui valut le Prix Nobel de Physique 1993 à Russel Hulse et Joseph Taylor.
En ce qui concerne les étoiles individuelles, les étoiles à neutrons en rotation rapide peuvent être déformées par des champs magnétiques, posséder une écorce boursouflée de montagnettes, subir diverses instabilités telles qu’oscillations, tremblements, glitches, etc., qui toutes engendrent des ondes gravitationnelles de très faible puissance. En contrepartie, il y en a au moins 100 000 dans notre seule galaxie.
De fait, la puissance d’une onde gravitationnelle reçue se mesure par son amplitude, c’est-à-dire par la variation relative de l’espace au passage de l’onde. Par exemple, si deux points de l’espace séparés de 1 kilomètre bougeaient de 1 millimètre au passage d’une onde gravitationnelle, l’amplitude de l’onde serait de 1 millimètre/1 kilomètre, soit 10-6. Or, les sources astrophysiques d’ondes gravitationnelles n’offrent que des amplitudes extraordinairement plus faibles ; celle engendrée par une étoile en rotation rapide est inférieure à 10–24 !
Les événements catastrophiques survenant à la fin de la vie thermonucléaire des étoiles massives peuvent produire des ondes de plus copieuse amplitude. Une explosion de supernova ou d’hypernova conduisant à la formation d’une étoile à neutrons ou d’un trou noir est a priori efficace ; astres relativistes par excellence, les trous noirs sont les sources potentiellement les plus prolifiques de rayonnement gravitationnel. Lorsqu’une étoile massive s’effondre pour former un trou noir, ses irrégularités (écart à la symétrie sphérique, champ magnétique, etc.) engendrent des “aspérités” dans l’horizon des événements ; le jeune horizon vibre alors de manière à évacuer ces aspérités sous forme d’ondes gravitationnelles : le trou noir perd ainsi ses « poils » pour tendre vers l’état d’équilibre de Schwarzschild (s’il ne tourne pas) ou de Kerr (dans le cas général).
La formation d’un trou noir à l’équilibre se fait ainsi en deux phases, chacune génératrice d’ondes gravitationnelles particulières ; il y a d’abord la phase d’effondrement proprement dit, conduisant à la formation de l’horizon des événements, aussi distordu soit-il. Ensuite, lorsque le jeune trou noir perd ses poils, il émet d’autres ondes gravitationnelles caractéristiques, aux fréquences particulières et dont l’amplitude diminue rapidement au cours du temps. Ces modes de vibration ont été baptisés « modes quasi normaux ». Si le trou noir tourne lentement, la fréquence du mode quasi normal varie comme l’inverse de la masse, et le temps d’amortissement est proportionnel à la masse. Ainsi, un trou noir de 10 MS émet un mode dominant à la fréquence de 1,21 kilohertz avec un temps d’amortissement de 0,55 milliseconde. En revanche, un trou noir de 1 million de masses solaires au cœur d’une galaxie émet ce même mode à la fréquence de 12,1 millihertz et un temps d’amortissement de 55 secondes. L’amplitude des modes quasi normaux dépend de la quantité de poils que le trou noir a à perdre ; elle est donc comparable à l’amplitude des ondes gravitationnelles émises dans la phase d’effondrement proprement dite.
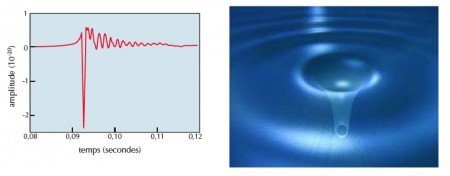
Hélas, contrairement à ce que l’on croyait il y a une vingtaine d’années, l’amplitude de l’onde gravitationnelle résultant d’un effondrement en trou noir est faible : au mieux 10–22 pour un événement survenant à 60 millions d’années-lumière, c’est-à-dire dans l’une des nombreuses galaxies de l’amas de la Vierge. Cette amplitude maximale, obtenue pour une rotation très rapide, représente à peine quelques millièmes de l’énergie totale libérée par l’effondrement (émise essentiellement sous forme de neutrinos).
Contrairement aux étoiles binaires, qui émettent des ondes gravitationnelles périodiques et que l’on pourrait assimiler à des « pulsars gravitationnels », les supernovae sont des sources impulsionnelles, produisant une brève et unique bouffée de rayonnement gravitationnel. Une autre source impulsionnelle est la coalescence d’étoiles binaires compactes, impliquant des étoiles à neutrons, mais aussi et surtout des trous noirs. La luminosité gravitationnelle de deux trous noirs de 10 masses solaires entrant en collision est 100 millions de fois plus grande que la luminosité électromagnétique du plus puissant quasar !

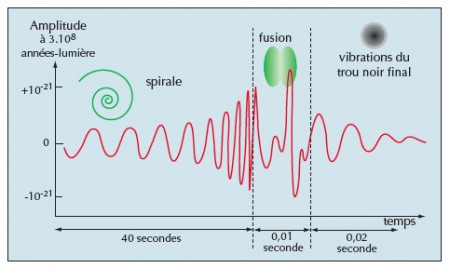
Les systèmes binaires de trous noirs résultent soit de l’évolution d’un couple d’étoiles massives, soit de la fusion de deux galaxies possédant chacune en leur centre un trou noir supermassif. Deux corps en orbite autour de leur centre de masse sont stables en mécanique newtonienne, mais pas en relativité générale : la courbure qu’ils engendrent se déplace avec eux sous forme d’ondes gravitationnelles ; en quittant le système, ces ondes emportent de l’énergie et les orbites des trous noirs se resserrent. À mesure qu’ils se rapprochent, la vitesse orbitale des trous noirs augmente, le taux d’émission gravitationnelle croît, et le processus s’emballe jusqu’à la fusion des deux trous noirs en un trou noir plus gros.
Lorsque les ondes émises par un système de deux trous noirs de 10 masses solaires chacun pénètrent dans la bande passante d’un détecteur, la distance qui sépare les trous noirs vaut 1 400 km. Environ 40 secondes (soit 600 orbites) plus tard, la fréquence atteint 200 hertz, la séparation n’est plus que de 180 km, les effets relativistes sont tels que le mouvement orbital en spirale devient instable ; les deux trous noirs plongent l’un vers l’autre en quelques millisecondes pour la fusion finale. Le signal gravitationnel perd sa régularité et sa forme n’est pas encore correctement calculée par la théorie. En revanche, dans la dernière phase de coalescence, le trou noir final perd ses poils par les modes quasi normaux, dont l’amplitude et la fréquence ont pu être calculées numériquement.
L’amplitude des ondes gravitationnelles émises par la coalescence de deux trous noirs est d’environ 10–21 à une distance de 300 millions d’années-lumière. Les modèles d’évolution stellaire prédisent l’occurrence d’une coalescence de trous noirs tous les 100 000 à 500 000 ans dans une galaxie donnée. Compte tenu du million de galaxies situées à moins de 300 millions d’années-lumière, on s’attend à détecter quelques événements chaque année…
On voit donc émerger une nouvelle astronomie aux exigences extrêmes, celle de la lumière gravitationnelle. Ce sera une astronomie d’une transparence incomparable, car, au contraire de la lumière électromagnétique, la lumière gravitationnelle n’est pas absorbée par la matière ; issue de sources lointaines, elle peut parvenir à la Terre en conservant toute l’information sur la configuration des sources qui l’ont engendrée. De plus, les sources les plus prolifiques sont justement celles sur lesquelles l’observation électromagnétique n’apporte qu’une information sommaire et indirecte : couples d’étoiles à neutrons, cœur de supernovae, trous noirs. Voilà pourquoi l’astronomie gravitationnelle ouvrira une fenêtre sur l’Univers le plus mystérieux, permettant non seulement d’accéder aux propriétés inconnues des astres compacts et de la matière ultra-dense, mais aussi d’assister enfin aux débuts de l’Univers, il y a 14 milliards d’années. Car l’Univers primordial, continuellement agité de fluctuations de densité, et le big bang lui-même ont été de puissantes sources de rayonnement gravitationnel ; et si les premières ondes électromagnétiques n’ont pu émerger que 400 000 ans après le big bang, le rayonnement gravitationnel, lui, a été engendré 10–22 seconde après le big bang, il a traversé sans encombre les états les plus denses de l’Univers primordial et il nous parvient aujourd’hui sous forme d’un rayonnement gravitationnel de fond, analogue au rayonnement électromagnétique fossile qui nous a déjà appris tant de choses sur la nature de notre Univers (voir chapitre suivant).
Ainsi, la lumière gravitationnelle fournira peut-être la seule preuve définitive de l’existence des trous noirs, ainsi qu’une connaissance détaillée des conditions extrêmes ayant régné lors du big bang.
Suite : De la barre à l’interféromètre

La cause de la gravitation universelle peut elle avoir une autre origine que celle de la matière possédant une masse ? En vertu de l’équivalence masse-énergie on pourrait soutenir que l’énergie de rayonnement est équivalente à une masse/c²……et engendre de la gravitation . Si ce n’est pas le cas comment interpréter le fait que les champs scalaires de Higgs avant la brisure de symétrie du modèle BEH auraient pu exister dans un univers de particules sans masse, cela signifierait qu’avant les 380 000 années post B.B. l’univers n’était pas soumis à la gravitation. A contrario ,si c’était le cas il faut concevoir une univers opaque de rayonnement gravitationnel, or que je sache le photon n’est pas censé pouvoir génerer un micro champ gravitationnel, et ce d’autant plus qu’il se déplace à la vitesse du graviton .
C’est bel et bien l’énergie sous toutes ses formes qui engendre la gravitation (je mets à part l’énergie sombre, qui engendre de l’anti-gravitation), et pas seulement l’énergie “condensée” en masse. L’univers primordial éait donc tout autant soumis à la gravitation, même avant la brisure de symétrie BEH conférant une masse aux particules. Merci de me lire.
Bonjour, c’est bien dommage que l’on ne puisse pas imprimer en Pdf…
erreur de ma part, je n’avais pas vu la petite croix orange…
Bonjour,
Très belle explication et accessible, j’en conseille vivement la lecture à tous. Je souhaitais juste faire une remarque sur la comparaison avec l’électromagnétisme. Vous montrez très clairement les différences entre ces deux modélisations qui sont d’ailleurs une des difficultés pour les unifier.
Mais il n’est pas totalement inintéressant malgré tout de regarder aussi les similitudes/proximités (je rebondis sur votre phrase “mais elle ne conduit guère plus loin”).
Par exemple, on ne peut encore exclure l’existence de la masse pesante négative. Des expériences (comme celle d’AEgIS au CERN pour ne citer qu’elle) pourraient très bien démentir cet “a priori”. Les similitudes avec l’électromagnétisme pourraient aussi aider à interpréter certain mystère comme la matière noire ou l’énergie noire. Je vous propose en guise de réflexion la lecture des 2 articles suivants: ARXIV:1503.07440 [http://arxiv.org/abs/1503.07440] et [https://hal-ens-lyon.archives-ouvertes.fr/ensl-01122689]
Bien cordialement
Bonjour et merci de me lire. Vous m’aviez déjà signalé il y a quelques mois vos deux articles très originaux, je m’excuse de ne pas y avoir répondu ni même les avoir lus, faute tout simplement de temps. Avez-vous pu les publier en revue, avec des avis de referee ? Cordialement et bonne continuation.
Bonjour,
je n’ai jamais appris autant de choses qu’en lisant “le destin de l’univers” et je vous en remercie.
Sachant que nos premiers pas dans le monde des ondes gravitationnelles a été franchi tout récemment, j’attends avec impatience vos commentaires sur la forme du signal détecté en rapport avec ce que prédisait la théorie, et sur la compréhension du phénomène qui l’a généré…
Bonjour
peut-on telecharger tout le dossier? en PDF?
Merci, c’est formidable comme blog
T.
En bas de chaque article il y a de petites icones, la première symbolise une imprimante, la seconde le partage sur facebook, la troisième le mail, etc. Pour l’article en pdf il faut cliquer sur l’icône imprimante, puis régler votre boîte de dialogue impression afin d’enregistrer un pdf plutôt quede faire une impression.
Bonjour,
A la lecture de la courbe de décroissance de la période du pulsar binaire, je comprends que la période a diminué d’environ 25 secondes en 25 ans. La période étant de 7,75 heures, 25 ans représentent environ 28.000 périodes. La décroissance serait de moins de 1ms par période. Par contre, le commentaire de ce graphe indique une diminution de 3 minutes par orbite. D’où vient cette différence ?
Merci pour vos articles.
Merci pour votre perspicacité, j’ai corrigé la légende où il y avait une confusion : la période diminue de 76,5 microseconde par an, c’est le grand-axe de l’orbite qui diminue de 3 mètres par orbite.
Je vous remercie pour votre réponse. Je retrouve votre site à la faveur des dernières détections.
Toujours au sujet de la courbe de décroissance de la période du pulsar binaire PSR 1913+16 , comment faire le lien entre la légende «… voit sa période orbitale diminuer de 76,5 microseconde par an » et la pente de cette courbe où l’on voit une décroissance de l’ordre de 2 secondes par an ? (Si je fais un calcul de cumul des décroissances par orbite, il y en a 1130 par an, je trouve un cumul de 4 centièmes de seconde par an, et non 2 secondes)
Il est vrai que la figure reproduite d’après l’article original de Taylor et Weisberg et sa légende prêtent à confusion, avec le terme “cumulative shift period”, et vous n’êtes pas le seul à vous être étonnés des valeurs numériques. Mais la figure et la légende sont justes! La réponse détaillée se trouve sur https://astronomy.stackexchange.com/questions/7974/hulse-taylor-binary-pulsar-how-is-cumulative-periastron-time-shift-calculate
les bras m en tombent !
Bravo pour vos travaux. Ce sont des recherches très difficiles. Je suis impatient de savoir ce que sont vraiment (pas en théorie) trous noirs et énergie sombre: “Ainsi, la lumière gravitationnelle fournira peut-être la seule preuve définitive de l’existence des trous noirs” tous le monde semble croire aux trous noirs alors que ce n’est pas prouvé !
Donc si je comprends bien, non seulement l’interaction gravitationnelle se propage à une vitesse finie (= notre bon vieux C), mais en plus le graviton est lui-même source de gravitation et de ce fait il doit être lui-même sensible à la gravitation (en tous cas le photon l’est, et je ne vois aucune raison pour que le graviton ne le soit pas).
Ok, parfait, bravo, mais qu’arrive-t-il aux gravitons aux abords d’un trou noir, voire lorsqu’ils sont émis par la singularité centrale ? Puisque franchir l’horizon des événements demande une vitesse supérieure à celle de la lumière, les gravitons devraient, eux aussi, ne pas pouvoir s’en sortir, et donc, les trous noirs ne devraient exercer absolument aucune influence gravitationnelle sur leur environnement. Pourtant, ils en exercent une, et pas une petite.
Quelqu’un aurait-il l’amabilité de m’expliquer ?
En attendant une réponse de JP LUMINET …
– L’existence du graviton n’est pas acquis. Pour l’instant rien ne prouve qu’il existe.
– Un trou noir exerce une influence gravitationnelle dû à sa masse, mais seul, il n’émet pas d’onde gravitationnelle.
– Il est possible que les ondes gravitationnelles soient, elles aussi, influencées par les masses comme le sont les ondes électromagnétiques, sujettes aux «lentilles gravitationnelles» par exemple. Mais, de même que la multitude des masses qui nous environnent ne nous empêche pas de voir les étoiles lointaines, on mesure des ondes gravitationnelles non perturbées.
Bonjour,
Merci pour la qualité de vos ouvrages de vulgarisation, que je connais depuis la lecture de “Les trous noirs” (éd. 1992), un livre qui présente la physique de ces objets de manière très claire pour un profane tout en restant rigoureux et complet sans tomber dans une simplification réductrice.
Aujourd’hui je me pose tout de même une question : comment peut-on être sûr d’avoir vraiment détecté des ondes gravitationnelles ?
Je comprends le principe de fonctionnement d’un interféromètre et je pense avoir une idée de ce qu’est une onde gravitationnelle (en ce qui me concerne je connais les équations de Maxwell et pour me faire une représentation d’une onde gravitationnelle résultant des équations de la relativité générale, je fais un parallèle avec les ondes électromagnétiques résultant des équations de Maxwell, tout en étant conscient des limites d’une telle analogie ; mes connaissances limitées en mathématiques font que je ne maîtrise absolument pas le calcul tensoriel).
Mais quand je lis que l’amplitude des déplacements détectés par l’interféromètre est excessivement faible (inférieure au diamètre d’un proton) je ne comprends pas comment on peut être sûr que ces déplacements sont bien dus à des ondes gravitationnelles et non à d’autres causes, comme p.ex. des mouvements géologiques, ou du bruit dans les appareils.
Auriez-vous l’amabilité de m’éclairer ? Merci.
Merci pour votre appréciation. En ce qui concerne la détection des OG, il va de soi que toutes les autres causes susceptibles de donner un signal autre que gravitationnel sont prises en compte, y compris un micro-séisme à l’autre bout de la planète. C’est ce qui rend la performance technologique particulièrement impressionnante. Par ailleurs le signal reçu est parfaitement conforme à ce que prédisaient les modèles théoriques de la fusion de trous noirs, ce qui ne serait pas du tout le cas s’il y avait du bruit parasite. On peut donc vraiment avoir confiance en l’interprétation des observations des interféromètres LIGO/VIRGO, d’autant que depuis le billet que vous avez commenté il y a eu plusieurs autres détections d’événements analogues.
Bonjour Monsieur LUMINET
Le détecteur d’ondes gravitationnelles c’est passionnant mais la comparaison de prix que vous faites avec un avion ou un lancement de satellite me parait inexacte , on nous cache souvent les coûts de “ces jouets” pour scientifiques.
En raisonnant de façon bassement matérielle, ne serait il pas grand temps de définir les priorités dans la recherche, ce domaine tout comme la détection du boson de HIGGS ou des neutrinos ,pour ne citer que quelques gouffres financiers, dont les français n’en voient pas toujours l’utilité , ne pourraient-ils pas être mis en sommeil au profit de la recherche médicale qui pleure souvent par manque de crédits pour ses équipements etc etc…
Salutations distinguées.
J. CHANTRENNE
C’est en effet très bassement matériel, ainsi que le veut le monde d’aujourd’hui, et il est bien dommage que vous tombiez dans ce type de raisonnement simpliste, qui n’est pas neuf. Savez-vous que l’imagerie médicale (entre mille autres applications) s’est développée à l’occasion du programme Apoollo il y a 50 ans, déjà fortement décrié pour son coût ? Mais qu’importe les retombées technologiques ! Pour moi : « Quel est le but qui vaudrait que l’on choisît de naître plutôt que de ne pas exister ? Spéculer sur le ciel et sur l’ordre du cosmos entier »
Anaxagore, Ve siècle av. J.-C.
Merci de me lire quand même.
Bonjour M.Luminet, et bravo pour votre blog, quel boulot!
Je suis content de l’avoir trouvé (via futura) pour vous soumettre un truc qui me taraude sur les ondes gravaitationnelles : nous savons depuis Einstein et Eddintgon que la lumière est sensible aux distorsion d’espace temps, comment donc la lumiere peut elle “reperer” les variations de longueur des bras d’un LIRGO puisque la “règle” qui les mesure se déforme aussi lors du passage des OG (pour mesurer un écart de longueur la regle ne doit pas se deformer avec l’objet qu’elle mesure sinon la longueur sera constante), or la lumière y est sensible (aux deformations d’espace) . Mais si j’admets que la lumière n’y est pas sensible, puisqu’elle permet de mesurer les variation de longueur des objets qui y sont “fixés” , c’est que la lumière n’est pas “fixée” à l’espace temps, dans ce cas dans quoi se déplace t elle puisque ce n’est plus l’espace temps qui la “supporte”?
Bonjour Monsieur Luminet,
Comme tant dit, un article exceptionnellement bien formulé et à la portée de tout curieux.
Encore merci de participer à la recherche et la diffusion de la connaissance. D’autant que celle-ci est palpitante : l’Univers.
Avec hâte, je m’en vais lire vos autres articles.
Merci.
Liva
Bonjour,
D’abord merci à vous pour vos apports d’informations claires, dans le cadre de la physique (relativiste et quantique). J’ai abordé ce sujet, et proposé un nouveau paradigme que j’ai voulu être compréhensible par tout un chacun (le paradigme du Nautile)*. D’ailleurs, vous êtes cité dans l’un des paragraphes (chapitre 6 : Interprétation des données physiques). Mon point de vue est que les ondes dites gravitationnelles n’aurait jamais due avoir ce qualificatif. Ce ne sont que des ondes spatio-temporelles qui module et créé le temps. La gravitation n’est qu’une des conséquences de cette modulation du temps. Bien sûr on peut faire un raccourci, mais cela change beaucoup de choses. Par exemple la modulation du temps peut expliquer pourquoi un électron est moins massif qu’un neutron ou un proton. C’est aussi le cas de l’anomalie constatée sur les distances parcourues par les sondes Pioneer ou les différents qui opposent plusieurs physiciens sur le redshift, l’expansion de l’Univers et la matière noire. Et là je ne site que quelques cas. Le chapitre 8 (Bilan) fait le récapitulatif de ces divergences.
Cordialement
– * http://www.universstrobofractal.fr
Sujet vitesse de la lumière
Bonjour,
Nous ne pouvons pas dépasser la vitesse de la lumière. Je crois que plus personne ne doute de ce fait. Cependant qu’est-ce qu’une vitesse ? D’une façon la plus élémentaire cela se traduit par la formulation suivante : v=e.t (espace x temps). Tout le monde appréhende facilement ce qu’est un espace, même dans le monde animal. Il faut tout de même faire une approche en fonction de la nature de cet espace (air, liquide, métal…). Pour la lumière il s’agit du vide. Le vide se trouve partout même dans la matière. Nous-mêmes, sommes composés essentiellement de vide (plus de 99,9%). Et pourtant nous ne sommes pas transparents pour autant. Mais c’est un autre sujet de discussion. Revenons à notre formule v=e.t. Le deuxième facteur est le temps. Quelle est sa nature profonde, pourquoi existe-il,
a-t-il une forme ? Autant de questions à ce jour non élucidées. En revanche, on l’a décortiqué pour s’adapter aux théories physiques utilisées ou à nos besoins quotidiens (temps propre, le temps apparent, le temps relatif, le temps absolu, le temps réel, temps imaginaire, temps universel, le temps atomique…) Ce dernier est à mon avis le seul à définir le temps le plus représentatif. C’est celui fourni par les horloges atomiques. Nous pouvons donc nous fier parfaitement aux mesures faites avec ce principe. Cela ne nous dit pas pour autant quelle est sa nature profonde et sa genèse. Pour ce qui est du temps que nous percevons le temps n’est qu’une interprétation des changements. Pour faire simple disons que si plus rien ne bouge, la notion de temps disparaît. Si quelque chose bouge (le soleil d’est en ouest) nous concevons alors la notion de temps. Notre univers n’est fait que de changements d’état. Il se dilate, les galaxies se déplacent et même les électrons gravitent autour du noyau de l’atome. Dans le cadre de la théorie de la relativité, le mouvement a bien été intégré au temps. Plus nous nous déplaçons vite plus le temps se dilate. Mais que se passerai-il si nous pouvions rester totalement immobiles au beau milieu d’une galaxie dans laquelle tout est en mouvement (comme celui que nous observons) ? Bien que nous soyons totalement immobiles nous aurions non seulement un temps du type que je qualifierais de banal, et ce en raison des différents mouvements autour de nous mais nous aurions aussi un temps propre. Ah bon ! Nous même alors que nous ne faisons aucun mouvement ! Comment se fait-il ? Tout simplement parce que nous sommes un assemblage d’atomes et qu’au niveau subatomique le temps généré par les replis spatiotemporels propre au point où je vis, n’est fait que de fréquences réglées en fonction de la configuration de la galaxie dans laquelle je me trouve. Ce temps je l’ai nommé : Temps Discontinu Quantique Relatif T.D.Q.R. ). Il est discontinu car sa « fréquence » varie entre le bord de la galaxie et l’horizon de son trou noir. Il est quantique en raison de la forme de cette fréquence (une avancée liée à la vitesse d’expansion de l’Univers et un retour infinitésimal). Relatif car il dépend non seulement de ma vitesse de déplacement mais du point où je me trouve. Cette forme de temps contribue à l’émergence de la masse d’un objet. Alors pour revenir au sujet principal de la discussion à savoir : la vitesse de la lumière est-elle une constante ? la réponse est oui.
Mais attention si vous êtes dans notre système solaire vous mesurerez 299 792 458 m / s.
Si vous avez la possibilité de faire la même mesure au milieu de la galaxie vous mesurerez 149896229 m/s. Enfin si vous êtes positionné sur l’horizon de notre trou noir (Sagittarius A*) vous mesurerez 0 m/s.
Si ce nouveau paradigme vous intéresse voici le site où il est traité sous forme de vulgarisation. http://www.universstrobofractal.fr
Théorie très très intéressante !!!