Sequel of the previous post Geometry and the Cosmos (2): From the Pre-Socratic Universe to Aristotle’s Two Worlds
Ptolemy’s Circles
Any model of the universe must incorporate the mechanisms determining the motion of the planets and other celestial bodies. From Plato and Aristotle to Kepler, astronomers could not imagine the universe governed by shapes other than circles and spheres, the only geometric forms that could possibly represent divine perfection. This constraint forced them to devise extremely complex systems which would “fit the facts”, in other words account for the apparent movements of the planets and stars as observed from the earth while conforming to the ideological demands of the concept of universal harmony.
Despite the ingenuity of astronomers like Euxodus (see previous post), their circular systems did not accurately describe the complex movements they had observed: the planets accelerated and decelerated and even occasionally went back the way they had come. Moreover, they did not account for the changes in brightness of the planets, which suggested variations in their distance from the earth that were incompatible with the idea that they travelled in circles centred on or near the earth.
How could Aristotelian cosmology be reconciled with astronomical observation? The most elaborate attempt to do so was made by Ptolemy (Claudius Ptolemaeus) in the second century AD. In his Syntaxis Mathematicae, better known by its Latin title Almagest, the Alexandrian thinker succeeded in explaining the motion of each celestial body by a system of extremely elaborate mathematical constructs.

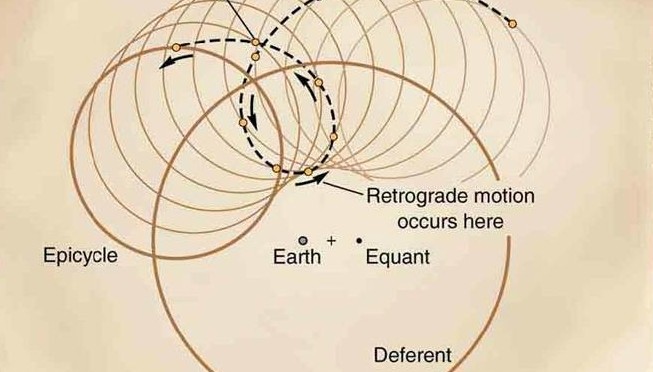
Ptolemy adopted the concept of a stationary earth and celestial bodies which could move only in circles. But he multiplied the number of circles and offset them one against the other, proposing complex and ingenious interactions between them. The circle in which a planet moves, called its epicycle, no longer had the earth at its centre as in Eudoxus’ theory, but itself revolved around another circle, called the deferent (or eccentric circle if its own centre is offset from the earth’s position). This theory enabled Ptolemy to “fit the facts” without departing too far from Aristotelian philosophical principles and it survived for 1,500 years — longer than any other idea in the history of science – until the discovery of elliptical orbits by Kepler.
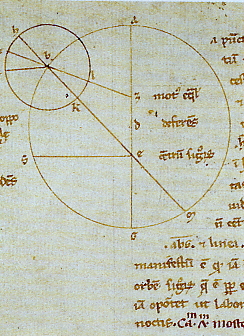
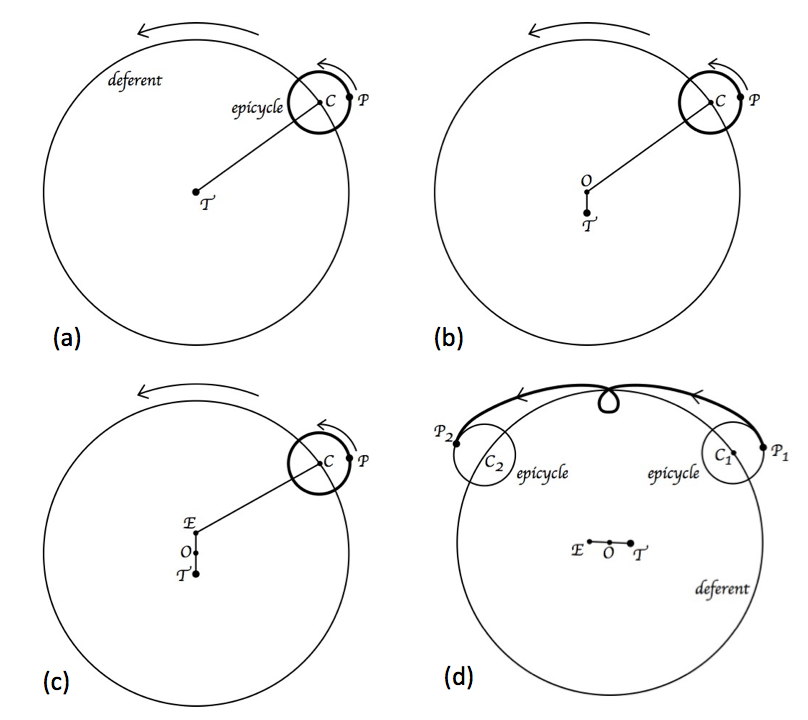
The Ptolemaic system was based on three geometric patterns: the epicycle, the eccentric circle and the equant. The epicycle had been invented in the third century BC by Apollonius of Perga, a brilliant mathematician whose most famous work is a treatise on conical sections (ellipses, parabolas and hyperbolas), and developed by Hipparchus a century later.
(a) Epicycle : a planet P rotates in a small circle (epicycle) whose centre (C) is simultaneously moving along the circumference of a large circle, known as the deferent, with the earth (T) at its centre.
(b) Eccentric Circle : the earth is offset from the centre (O) of the deferent. This model breaks the Aristotelian rule which states that the earth must be at the centre of the cosmos.
(c) Equant : despite its complexity, the eccentric circle model does not provide a sufficiently accurate explanation of the apparent motion of the planets. Ptolemy therefore postulated an equant point (E) about which the centre of the epicycle (C) rotates. Both the geometric centre of the deferent (O) and the centre of motion are now offset from the earth’s position (T).
(d) Final Model : the Ptolemaic model plots the motion of the planets according to this sytem, but it was so complicated that it was not fully understood by Western civilisation until the 15th century.
Ptolemy proudly defended its complexity: “We must as far as possible apply the simplest hypotheses to the movements of celestial bodies but, if these are inadequate, we must find others which explain them better.” (Almagest, XII, 2) – a statement which placed him firmly in the vanguard of modern scientific thinking.
Nevertheless, the system of epicycles and eccentric circles suggested that the earth was not exactly at the centre of the cosmos and Islamic astronomers raised several objections to this infringement of Aristotelian harmony. It was the existence of an equant point offset from the earth that particularly preoccupied later scientists. Copernicus, for example, in his De Revolutionibus announced his intention to rid the celestial model of this “monstrosity”.
Islamic Objections to the Ptolemaic System
The journey of the prophet Muhammad to Medina in 622 AD marked the beginning of the rapid and turbulent expansion of Islam. The new dynasty of Abbasids founded their capital, Baghdad, in 762 and set about translating the great Greek texts of Aristotle, Euclid, Ptolemy, etc. In 813 Caliph Al-Ma’mun founded the “House of Wisdom”, an academy where people of different cultures could mingle in a completely liberal environment.

The greatest translator of Greek, Thabit ibn Qurra, also wrote more than 100 scientific treatises, including a commentary on Ptolemy’s Almagest. Around 1110 the Englishman Robert of Chester, who was then in Spain, translated into Latin al-Jabr (Algebra) by the astronomer and mathematician Al-Khwarizmi and introduced into Europe Arabic numerals, including the figure zero, which the Arabs themselves had borrowed from the Indians. Another scientist from the academy, Ahmad Al-Farghani, popularised Ptolemaic astronomy through his book The Elements, whose influence on Western thought was considerable: two Latin translations were made in the 12th century, by John of Seville and Gerard of Cremona (the latter being the source of Dante’s astronomical knowledge, expressed in his Vita Nuova and The Banquet), and it was taught at the University of Padua in 1464 by Regiomontanus. One of the most important astronomical works between Ptolemy and Copernicus, al-Zij al-Sabi (known as the Sabian Tables), was written by Al-Battani, a contemporary of Thabit ibn Qurra. In it he plotted the sun’s orbit more accurately than Ptolemy. In his De Revolutionibus, Copernicus was to refer to Al-Battani’s calculations no fewer than 23 times.

Between the 10th and 13th centuries Arabic astronomers developed a system of spheres inspired by the Ptolemaic system but with the aim of correcting and improving upon it. Thabit ibn Qurrat compiled important tables of calculations. Ibn Al-Shatir based his astronomical tables on observations made from ancient Cairo and focused his attention to the planet Mars, whose sidereal motion is the most complex and therefore the most difficult to explain within the Ptolemaic system.
While maintaining a geocentric view of the cosmos, Islamic astronomers criticised technical details of the Ptolemaic system. In his Doubts About Ptolemy the eminent 11th century physicist Ibn-al-Haytham (Alhazen) challenged the use of an equant. At the same time, in southern Spain, the astronomer and philosopher Ibn Rushd (Averroes) rejected Ptolemy’s eccentric deferants in defence of a strictly concentric model of the universe. At the opposite end of the Islamic Kingdom Nasir Al-Din Al-Tusi was founding an observatory at Maragha (now in north-west Iran). In his Tadhkira fi ’ilm al-hay’a (An Essay on Astronomy) Al-Tusi removed the equant and added instead two small epicycles to the orbit of each planet, thereby describing irregular movements by combinations of circles around which the planets move regularly. The centres of the deferents, however, remained offset from the earth. Finally Ibn Al-Shatir, working in Damascus around 1350, extrapolated Al-Tusi’s ideas into a completely concentric and mechanically orthodox planetary system.
During the 13th and 14th centuries several Arabic and Persian astronomical works were translated into Greek by travelling Western scientists and part of the planetary system of the Maragha astronomers (including Al-Tusi) would later be adopted by Copernicus, whose Commentariolus would propound a system similar to that invented by Al-Shatir, but within a heliocentric framework.

Nasir Al-Din Al-Tusi, Tadhkira fi ‘ilm al-hay’a (“An Essay on Astronomy”), 1389. Paris, BNF, Manuscripts, Arabic 2509.
Ptolemy, Epicycles and Fourier analysis
In principle Ptolemy’s scheme, like the competing system of homocentric spheres proposed by Eudoxus and Callipus (endorsed by Aristotle) could be made as accurate as desired by the addition of more circles. In practice however, Ptolemy invented some very ingenious mathematical tricks to simplify the calculations, but these tricks did not lend themselves to extensions should further epicycles be added to the system. Furthermore, until the massive observational campaigns of the Danish astronomer Tycho Brahe in the late 16th century, no one had a sufficient database to make major revisions to the standard computational scheme handed down from Ptolemy.
During the Middle Ages various computing tables were assembled, one of the most famous and widely used being the Alphonsine Tables, commissioned by King Alfonso the Great in the thirteenth century. Legend has is that, on seeing the labours of his astronomers, Alfonso remarked that, if he had been present at the Creation, he could have given the Lord some hints making the motions simpler!
Early in the 19th century the French mathematician François Joseph Fourier demonstrated that any periodic motion could be described by a combination of circular motions. Eventually this gave rise to the mythology that something of the kind had actually taken place and that Alfonso had seen his astronomers struggling with epicycles-on-epicycles. Copernicus, at the end of his small prelimanary treatise, the Commentariolus, exclaimed “Behold, 34 circles suffice for the entire dance of the planets!”. His remark, intended to show that the complicated apparent motions of the heavens could be explained relatively easily, added fuel to the legend which, by the end of 19th century, had grown to wrongly attribute 80 circles to the enhanced Ptolemaic systems of the Middle Ages.
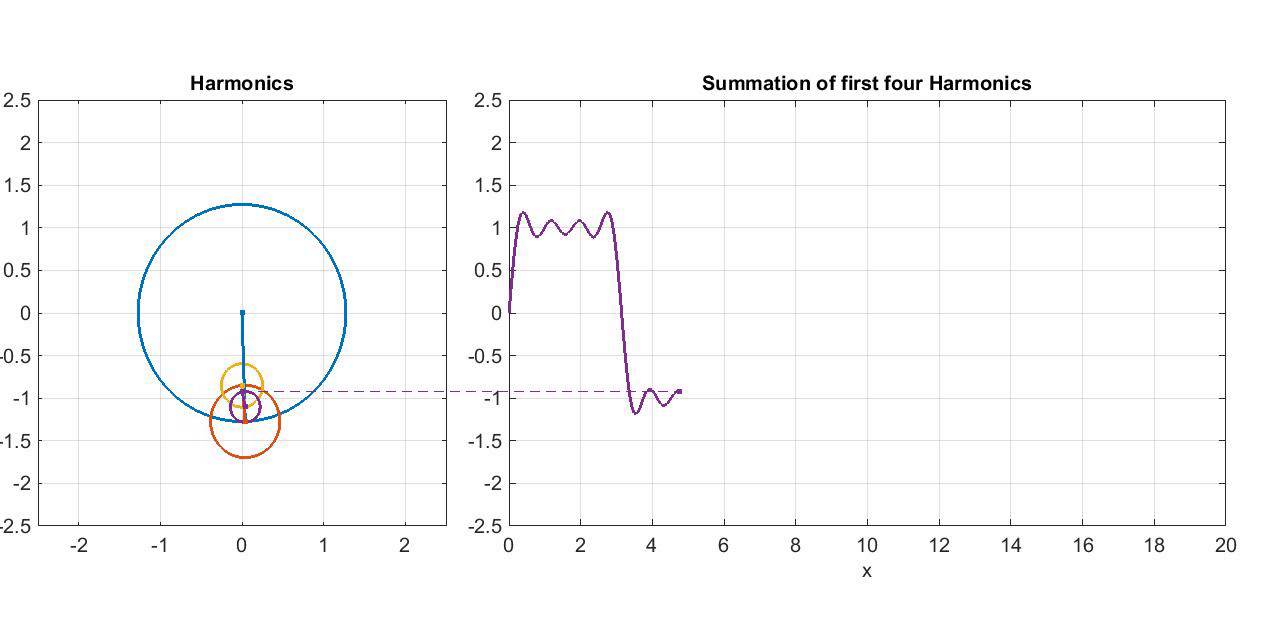
From Epicycles to Inflation
Ptolemy and his followers attempted to uphold the idea of circular movement, which was supported by metaphysical, religious, mystical and aesthetic arguments, while remaining true to the natural phenomena they observed. Nowadays the term epicycle, which is associated with the highly sophisticated Ptolemaic system, denotes excessive and unnecessary complexity introduced into a system in order to make it conform to a preconceived, extrinsic (and therefore unscientific) idea.
Modem physics is not without examples of this kind of thinking. Many physicists believe that certain problems in contemporary astronomy can be solved by the application of high-energy particle physics and, more generally, quantum physics. This approach, which is in keeping with a legitimate desire to unify the different fields of physics, has already met with some success, for example in relation to “dark matter”, the formation of galaxies, anti-matter, and the uniform distribution of matter throughout the universe. But it can be a mistake to pursue this line of thought too far.
This was arguably the case with the concept of “inflation”, which was developed in the late 1970s. Inflation was the term used to describe a hypothetical period (10-35 seconds) during which the early universe was supposed to have increased in size by a huge factor up to roughly 10100: in other words it would have expanded far more in that tiny fraction of a second than in the succeeding billions of years of cosmic evolution!
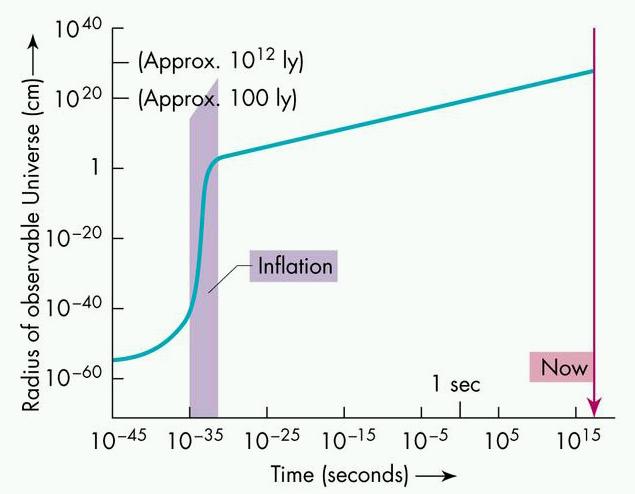
The idea was immediately attractive, but it had to be substantiated. During the 1980s physicists hoped to revitalise particle physics by finding a “grand unified theory”. A theory named SU(5), which added a new quantum field (the “inflaton”, also called “dilaton”) unlike those previously recognised, seemed to make inflation feasible. Overcome with euphoria, astrophysicists started examining the possible consequences of the idea despite the absence of a proper theory. The conclusions they reached by a priori reasoning were so encouraging that their enthusiasm for the scenario increased still further.
Unfortunately, theory SU(5) was unfounded and the dream of constructing a unified theory of this kind faded rapidly. Other attempts were unsuccessfully made and most of the physicists, clinging to the positive aspects of the idea of inflation, were nevertheless reluctant to renounce it altogether. In their eagerness to make it “fit the facts” in spite of everything, they devised ever more complicated versions of it: for example, they supposed the existence of new kinds of quantum fields to which they attributed the most precise characteristics on an ad hoc basis, just as the Ancient astronomers had done two thousand years earlier.
Interesting article! If you allow me a small remark, it seems you identify Ibn Al-Haytham as Al-Battani, although they are twxo distinct Muslim astronomers.
Al-Haytham (~965-~1039) is known to the West as Alhacen or Alhazen, whereas Al-Battani died in 929 and is known as Albategni.
Thanks for your careful reading, you’re perfectly right and I corrected the misprint.